Ballistic performance of tungsten particle/metallic glass matrix composite long rod

Ji-cheng Li ,Xiao-w ei Chen ,Feng-lei Huang

a State Key Laboratory of Explosion Science and Technology,Beijing Institute of Technology,Beijing,100081,China

b Institute of Systems Engineering,China Academy of Engineering Physics,Mianyang,Sichuan,621999,China

c Shock and Vibration of Engineering Materials and Structures Key Laboratory of Sichuan Province,Mianyang,Sichuan,621999,China

Keyw ords:Tungsten particle/metallic glass matrix(WP/MG)composite Ballistic performance Shear band Self-sharpening Numerical analysis

A B S T R A C T In the present manuscript numerical analysis on the ballistic performance of a tungsten particle/metallic glass matrix(WP/MG)composite rod is conducted by integrating with related experimental investigations.In the corresponding f i nite element method(FEM)simulations a modi f i ed coupled thermomechanical constitutive model is employed to describe the mechanical properties of metallic glass(MG)matrix,and geometrical models of the WP/MG composite rod are established based on its inner structure.The deformation and failure characteristics of the rod and target materials are analyzed in detail,and the in f l uences of various factors on the ballistic performance of the WP/MG composite long rod are discussed.Related analysis demonstrates that the penetrating performance of the WP/MG rod is similar to that of the tungsten f i ber/metallic glass matrix(WF/MG)composite long rod,i.e.,a“self-sharpening”behavior also occurs during the penetration process,and correspondingly its penetrating capability is better than that of the tungsten heavy alloy(WHA)rod.How ever,the mass erosion manner of the WP/MG rod is different and the erosion is relatively severe,thus its penetrating capability is a little low er compared with that of the WF/MG one.Moreover,the impact velocity and the target strength have signi f i cant in f l uences on the ballistic performance of the WP/MG composite rod,w hereas the effect of initial nose shape is very little.

1.Introduction

At present the kinetic energy penetrator(KEP)is mainly made of tw o kinds of materials,i.e.,the tungsten heavy alloy(WHA)and the depleted uranium alloy(DUA).One shortcoming of the WHA rod is that the high plasticity of WHA material usually leads to a blunted rod nose w ith a“mushroom”shape,and this w ill induce high resistance and further a reduced penetrating performance[1].Comparatively,the advantage of DUA rod is the“self-sharpening”behavior w hich is derived from its relatively high adiabatic shear sensitivity,and correspondingly it can achieve a better penetrating capability compared w ith the WHA rod[2,3].How ever,the DUA material w ill lead to radiation harm[3].Hence,during the last tw o decades the military research is alw aysexploring a new kind of KEP material w ith“self-sharpening”property and w ithout radiation harm[4-14].

Related research demonstrated that the tungsten f i ber/metallic glassmatrix(WF/MG)composite and the tungsten particle/metallic glass matrix(WP/MG)composite have good potential[5-9].Metallic glass(MG)is an amorphous alloy,and it has many excellent mechanical and physical properties[15-18].One of its important mechanical characteristics is the high shear sensitivity,i.e.,highly localized shear bands occur much more easily in MG during the deformation process,and thus its shear sensitivity is remarkably higher than that of traditional crystalline alloys[19-21].Moreover,after introducing the reinforced phases,e.g.,tungsten f i bers(WFs)or tungsten particles(WPs),the corresponding composites can integrate the excellent properties of the MG matrix(e.g.,high strength and high shear sensitivity,etc.)and the good characteristics of the tungsten reinforced phases(e.g.,good plasticity and high density,etc.)[22].Related penetrating experiments show ed that the MG matrix composite rods indeed display a signi f i cant“self-sharpening”behavior due to the high shear sensitivity of the MG matrix,and correspondingly they achieve a remarkable improvement of penetrating capability compared w ith that of the WHA rod[5-8].

In the high-speed impact experiment,the deformation and failure characteristics of the rod and target materials are usually dif f i cult to observe directly,and the inner parameters,such as rod velocity and stress state,etc.,are also hard to be directly measured.Consequently,the f i nite element method(FEM)simulation becomes an effective supplement.The simulation is usually valid and it is favourable for the deeper analysis on related experiments[9,23-26].The authors have conducted detailed analysis on the“self-sharpening”performance of a WF/MG composite long rod based on FEM simulations[9].In the corresponding research,the geometrical model of the WF/MG composite rod is established based on its inner structure,and a modi f i ed coupled thermomechanical constitutive model is employed to describe the high strength and high shear sensitivity of the MG matrix.Hence,the corresponding simulations depicted w ell the deformation and failure characteristics of the real rod and target materials.

The inner structure of WP/MG composite is signi f i cantly different from that of the WF/MG one,and correspondingly their deformation and failure features deviate from each other[27,28].Nevertheless,related penetrating tests demonstrated that the WP/MGcomposite rod also displays a“self-sharpening”property and it results in a better penetrating performance compared w ith the WHA rod[6].In the present manuscript FEM simulations and the corresponding mechanism analysis on the ballistic performance of WP/MG composite rod w ill be further conducted.Integrated w ith related penetrating experiments[5,6],tw o-dimensional(2-D)and three-dimensional(3-D)FEM simulations are implemented,and comparative analysis betw een the WHA rod and the WF/MG rod w ill also be conducted.Furthermore,in f l uences of various factors,including the impact velocity,the target strength and the initial shape of rod nose,on the ballistic behaviors of the WP/MG composite rod,are analyzed in detail.

2.Geom etrical models and constitutive models

2.1.Geometrical models

LS-DYNA softw are is employed to implement the FEM simulations.Generally speaking,a 3-D model could represent the actual structure of real composite better,and a 2-D simulation is convenient to investigate directly the deformation and failure process of materials.Thus,in the follow ing analysis both 2-D and 3-D simulations are conducted.

Regarding to the WP/MG composite,the reinforced tungsten particles distribute randomly in the MG matrix,and their sizes are usually not uniform.Thus,it w ill be onerous to establish the geometrical model of composite long rod in the pre-processing program by follow ing a normal procedure.Also,it w ill be dif f i cult to achieve a f i ne quality of meshes.The meshes w ill affect the accuracy of simulation result and the solution time of calculation[28].In the present manuscript,based on the format of keyw ord f i le in the LS-DYNA software and the FORTRAN program,the reinforced particles can be de f i ned conveniently in the FEM geometrical model and their random distribution is achieved at the same time.The LS-DYNA keyw ord f i le contains all related information for the calculation,w herein the element information section lists the detailed messages for each element in the geometrical model,including the element ID number,the part ID number to w hich the element belongs and the node ID number that belongs to the element,etc.Similarly,the part information section includes the part ID number and the material ID number,and the node information section contains the node ID number and the details of spatial coordinate for the node.Besides,these ID numbers correspond to each other uniquely.Thus,by changing the part IDnumber of an element one can change its material dependence correspondingly.

The approach to establish the geometrical models of reinforced particles is as follow:Firstly,de f i ne the spatial range for particles according to the dimension of composite rod in the FORTRAN program,and then randomly generate the spherical particles(circular particles for the 2-D model)w ithin the spatial range based on Monte Carlo algorithm.The corresponding information w ill include the parameters about the position as w ell as the diameter of the particles.Secondly,establish the geometrical model and the corresponding meshes of long rod w ithout the reinforced particles in the pre-processing program,and in this procedure relatively f i ne meshes can be obtained.Finally,integrated w ith related information about the particles and the corresponding meshes in the geometrical model,and by employing the mapping algorithm,the geometrical models of reinforced particles can be achieved.The corresponding implementation stages are listed below:

(1)Generation of reinforced particles Step 1 Input the dimension parameters of the composite long rod and de f i ne the spatial range of reinforced particles.Step 2 Calculate the number of reinforced particles.Step 3 Randomly generate the position of a particle w ithin the range of long rod,and de f i ne the corresponding diameter of the particle(w hich takes randomly a value of 70μm,50μm,30μm or 10μm)at the same time.Step 4 Check w hether the non-superposition boundary condition is satis f i ed to avoid overlapping among particles.Step 5 If the generated particle satis f i es the nonsuperposition boundary condition,record its corresponding parameters;otherw ise delete the particle and perform a new generation until the generated particle satis f i es the boundary condition.Step 6 Repeat steps 3-5 until the calculated number of reinforced particles is reached.

(2)Mapping of meshes for reinforced particles in the FEM geometrical model Step 1 Generate regular meshes of long rod w ithout reinforced particles.Step 2 Calculate the central coordinate of each mesh element.Step 3 Check the position of each element w ith respect to that of each particle generated in Stage(1)above.Step 4 If the element center locates in one of the particles,assign the element w ith particle material;otherw ise assign it w ith MG matrix material.

FEM simulations are conducted integrated w ith the corresponding penetrating tests[5,6].Choi-Yim et al.[6]conducted penetrating tests into aφ152 mm×102 mm 6061-T651 aluminum target,and the corresponding WP/MG composite rod w as a f l atnosed one w ith a size ofφ6.35 mm×38.1 mm,i.e.,the aspect ratio is L/d=6.The average diameter of reinforced WPs is 50μm,and their volume fraction occupies a value of 50%.Thus,the monolithic density of the composite achieves a value of about 14 g/cm3,being close to that of the WHA material(17.45 g/cm3).Comparatively,Conner et al.[5]conducted similar penetrating tests of WHA rod into the same aluminum target,and the aspect ratio of the rod is also L/d=6.The corresponding sketch of the penetrating test is show n in Fig.1.

Due to the axis-symmetry property of penetrating condition,the 2-D FEM simulation is set as the axis-symmetrical model,and the geometrical model is meshed w ith the 4-node axissymmetrical elements.The corresponding 2-D geometrical model of rod is listed in Fig.2(a),in w hich the zones labeled w ith“A-C”are the key points in the later analysis.The distances from points of“AC”to the nose tip are 1 mm,19 mm and 37 mm,respectively.Similarly,for the 3-D simulation only a quarter of the geometrical model is established,and the corresponding geometrical model of rod is shown in Fig.2(b),w hich is meshed w ith 8-node hexahedral elements.From Fig.2(a and b)it is seen that the tungsten particles distribute randomly in the MG matrix,and the average size of particle diameters is set as 50μm.It should be noted that the particle diameter is calculated from the corresponding number of meshes in the particles.The mesh size in the rod is set as 5μm,and these f i ne meshes could lead to good geometrical models of particles and consequently induce relatively accurate simulation results.Besides,the matrix and WPs are f i xed together through the nodes shared by these tw o parts.Fig.2(c)further show s the SEM micrograph of cross section of the real composite[6],and by comparing w ith Fig.2(a and b)it is found that the FEM geometrical models represent the structure of real composite relatively w ell.

Furthermore,related simulations on the WHA rod penetration are also conducted.For convenience of comparative analysis,the corresponding geometrical model of WHA rod is set as the same w ith that of the composite one,i.e.,the models in Fig.2(a)and(b),and only materials in both the particle and matrix parts are de f i ned as tungsten instead.

2.2.Constitutive models

2.2.1.Metallic glass(MG)

The shear deformation property of MGmaterial differsfrom that of the traditional crystalline alloys.The authors have developed a modi f i ed coupled thermo-mechanical model and a failure criterion of critical free volume concentration to describe the mechanical properties of MG[29,30],and the constitutive equations are listed in Appendix A.During the FEM calculation,once the failure criterion(Eq.(A4))is met,the failed element is deleted and removed from the geometrical model based on the“element killing”algorithm.

In the above composite rod the matrix is Zr-based MG.Integrated w ith related research[9,27-32],the corresponding material parameters are listed in Table A1,and the detailed analysis on the parameters can be seen in our previous investigations[29,30].

Fig.2.FEM geometrical models of WP/MG composite long rod,test datum is from Ref.[6].

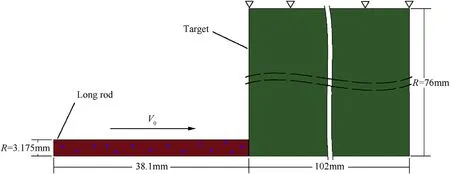
Fig.1.Sketch of penetrating test for the long rod.

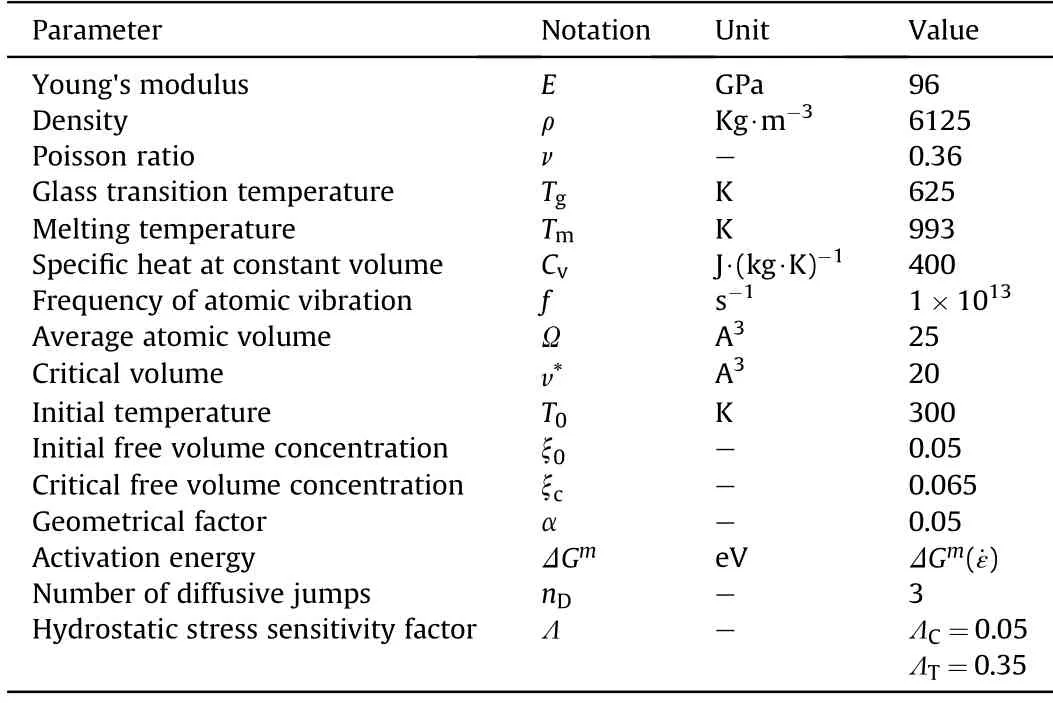
Table A1Parameters of Zr-based metallic glass[29,30].

2.2.2.Metals

WPs in the composite rod,the WHA rod and the 6061-T651 aluminum target belong to the traditional crystalline alloys.Similar to our previous analysis[9,27,28],the Johnson-Cook constitutive model[33]combined w ith the accumulative damage failure criterion[34]are still employed to describe the corresponding mechanical behaviors.At the same time,the pressure in the penetration process is calculated by the Gruneisen equation of state[35].The Johnson-Cook model can represent relatively w ell the mechanical behaviors of metals at different strain rates,and related constitutive equations are listed in Appendixes B and C,respectively.

Based on the mechanical properties of the rod and target materials in the above penetrating experiments[5,6],and integrated w ith related FEM analysis on the tungsten,aluminum and steel materials[9,23,27,28],values of Johnson-Cook model parameters for the tungsten alloy(93 W,i.e.,W93Ni1.4Fe5.6)and 6061-T651 aluminum are obtained and listed in Table 1.Besides,for comparative analysis on the in f l uence of target strength and for comparison betw een the WP/MGcomposite rod and the WF/MGcomposite rod,numerical analysis on the penetration into 30Cr Mn Mo steel target(the strength of this steel target is very high)w ill also be conducted.The corresponding parameters follow the authors'previous analysis[9]and they are also listed in Table 1.Similarly,the“element killing”algorithm is invoked to delete and remove thefailed element from the geometrical model w hen the failure criterion(Eq.(B3-B4))is met.

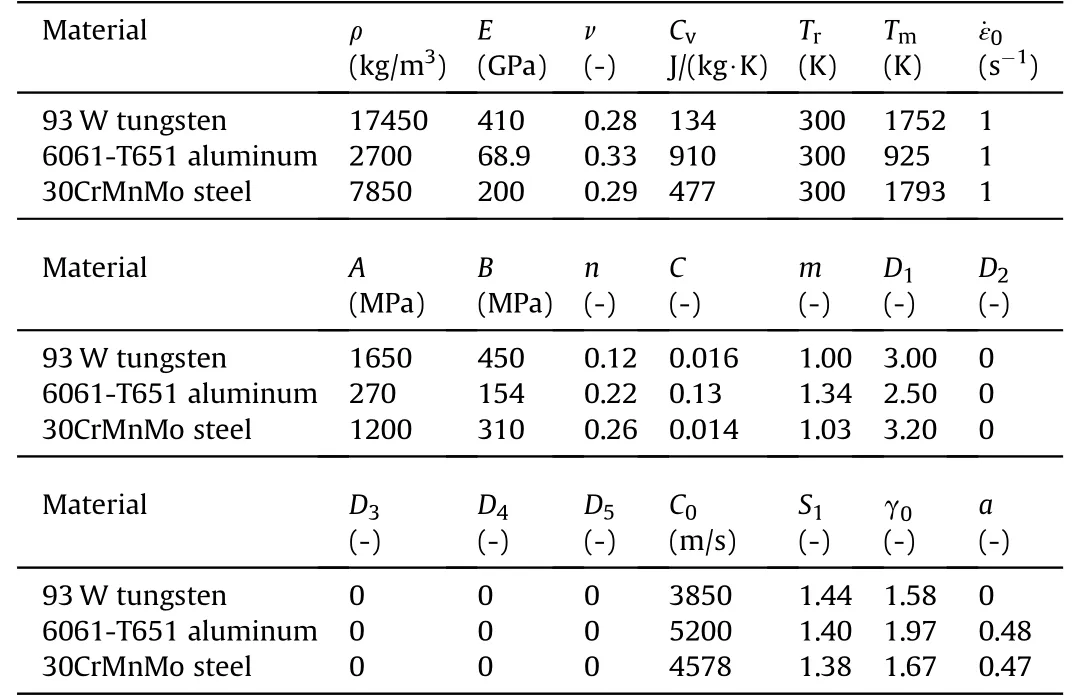
Table 1Johnson-Cook model parameters of metals.

3.Model validation and related analysis

Integrated w ith three typical penetration cases in Conner et al.[5]and Choi-Yim et al.[6]'s tests,the corresponding FEM simulations and related analysis are conducted.For comparative analysis betw een the simulation results and the test data,related test data are listed again in Table 2 and labeled w ith“T”.For the test data the length of real residual rod is measured from the images in the literature directly,and the measured data are labeled w ith the symbol of“*”.Comparatively,the simulation results in the table are labeled w ith“S”.

Figs.3 and 4 show the f i nal forms of rod and target for the penetrations of WHA rod into 6061-T651 aluminum target under the impact velocities of V0=694 m/s and V0=1060 m/s,respectively.It can be found from Fig.3 that due to the high plasticity of tungsten material,the nose of WHA rod blunts into a“mushroom”shape after the penetration,besides,some fragments separate from the rod nose and f l ow backwards.The mushrooming deformation of the rod nose leads to a relatively large penetrating hole in the target,and its diameter is remarkably larger than the diameter of the rod shank.Moreover,the blunted rod nose induces high resistance for the WHA rod,and thus the depth of penetration(DOP)is only about 39 mm(see Table 2).The rod erosion is also severe,and the residual length l is only about 21 mm.Comparatively,w ith increasing the impact velocity,the mushrooming deformation of the rod nose becomes more remarkable(see Fig.4),correspondingly the penetrating hole is also larger,and the DOPincreases to a value of about 62 mm.Besides,the rod erosion becomes more severe,and the length of residual rod is l=14.5 mm.

Similarly,the pattern for the penetration of the WP/MG composite rod at V0=998 m/s is listed in Fig.5.Different from the case of the WHA rod,because of the high shear sensitivity of the MG matrix,materials w ithin the nose of the composite rod experience extreme shear deformation and failure during the penetration process,and then further separate from the rod and f l ow backw ards.This leads to the“self-sharpening”deformation in the rod nose.Due to this“self-sharpening”behavior,the diameter of penetrating hole in the target is almost the same as that of the rod shank.Compared w ith the WHA rod in Fig.4,it is found that the sharp nose of the composite rod induces lower resistance,and thus the resulting DOPincreases considerably under the similar impact velocity,achieving about 89 mm(see Table 2).At the same time,the erosion of the composite rod is also less severe,and the corresponding length of the residual rod is 19 mm.

Besides,as show n in Figs.3-5,the 3-D simulation results represent the test data better compared w ith the 2-D results,e.g.,the scratch pattern in the penetrating hole(see Figs.3(b)and 4(b)and 5(b)).Nevertheless,the 2-D results also depict relatively w ell the main deformation and failure characteristics of the rod and the target.

Comparison betw een these tw o kinds of residual rods w ill be further conducted.Fig.6 lists the corresponding residual rods under the above penetrations,and it is seen again that the simulations depict the penetrating tests w ell.Though there is bending deformation additionally in the real residual WHA rod(see Fig.6(c)),the numerical results agree w ell w ith the test data for many aspects,e.g.,the mushrooming characteristic of rod nose and the length of residual rod,etc.Regarding to the composite rod,the numerical results also accord w ith the test data,especially for the sharp rod nose.

Besides,the nose of WHA rod becomes blunt,forming a“mushroom”shape,and the diameter of the shank near to the“mushroom”nose also increases considerably compared w ith its initial status.Additionally,under the higher impact velocity,the length of residual rod decreases at a certain extent(see Fig.6(d and e)and Table 2).This is due to that for the thick target,the rod material and target material interact w ith each other for a long duration in the penetration process,and thus the erosion of rod is more severe corresponding to the higher DOP[36].

Table 2Test data and the corresponding simulation results for penetrations into 6061-T651 aluminum target.

Fig.4.Numerical deformation and failure patterns of WHA rod and 6061-T651 aluminum target under penetration at V0=1060 m/s.

Fig.5.Numerical deformation and failure patterns of WP/MG composite rod and 6061-T651 aluminum target under penetration at V0=998 m/s.

Comparatively,regarding to the nose of the composite rod,the MG matrix undergoes extreme shear deformation and failure,and the shear bands or cracks impact onto the surrounding WPs and further induce signi f i cant shear deformation in the particle,or even some WPs are cut off.Finally,materials w ithin the nose separate from the composite rod,and the nose sharpens.Besides,there is only a slight deformation in the rod shank nearby the sharp nose.

Additionally,the penetrating capability of the WP/MG composite rod is better compared w ith that of the WHA rod under similar impact conditions,and the main reason is that the mushrooming deformation of the WHA rod leads to relatively high resistance w hereasthe“self-sharpening”behavior of the composite rod induces low er resistance.Besides,for the residual composite rod isslightly longer than the residual WHAone(see Table 2),it w ill maintain greater destructive potency for the objects behind the target if the target is perforated.

The above simulations and related analysisdemonstrate that the FEM simulations represent relatively w ell the penetrating tests,and thusthe corresponding analysisbased on the simulation resultshas good reference signi f i cance to the practical engineering.Besides,it is seen that 2-D simulation could also depict the main mechanical performances of the rod and the target.To investigate the deformation and failure of materialsdirectly and to reduce the amount of calculation,the follow ing analysis w ill mainly focus on the 2-D simulations.

4.Analysis on the mechanism for the ballistic perform ance

4.1.Deformation and failure characteristics of the rod and target materials

By comparing the deformation and failure characteristics betw een the WHA rod and the composite rod during the penetration process,the mechanism of related ballistic performance of the WP/MG composite rod w ill be discussed.The evolutions of effective strain in the rod and in the target for the WHA rod penetration at V0=1060 m/s as w ell as the composite rod penetration at V0=998 m/s are show n,respectively,in Figs.7 and 8,in w hich the magni f i cation of the rod nose during the initial and the middle penetrating stages are also displayed.

The nose of the WHArod becomes remarkably blunt in the early stage,and it induces a large penetrating hole in the target(Fig.7(a)).During the w hole later stage,fragments separate out from the blunted nose and f l ow laterally backwards,how ever,the rod nose always maintains its“mushroom”shape(see Fig.7(b)and(c)).

Comparatively,as show n in Fig.8,for the composite rod,in the early stage,because the MG matrix w ithin the rod nose has failed and the surrounding WPs experience extreme deformation and further separate from the rod(see Fig.8(a)),the rod nose is slightly less blunt compared w ith the WHA rod(see Fig.7(a)).During the latter stage,WPs continue the extreme deformation or even are cut off by the shear cracks from the MG matrix,and they further separate from the rod nose.Consequently,the nose tip further becomes as a sharp shape,and correspondingly the diameter of penetrating hole in the target is relatively small.

Fig.6.Residual rods after penetrations into 6061-T651 aluminum target,test data are from Refs.[5,6].

In the follow ing analysis,the deformation and failure of the rod nose w ill be investigated in detail.For the WHA rod,after the impact onto the target,shear cracks initiate in the front end of the f l at nose and then propagate obliquely tow ards the back end.How ever,due to the high plasticity of tungsten material,the propagation distance of the shear crack is relatively short.At the same time,there is extreme plastic deformation w ithin the monolithic rod nose,and because of the squeeze of target material,materials w ithin the lateral side and w ithin the tip of rod nose fail severely,as show n in Fig.7(d).During the later penetration process,the rod nose keeps the“mushroom”shape until the rod stops eventually(see Fig.7(e)).

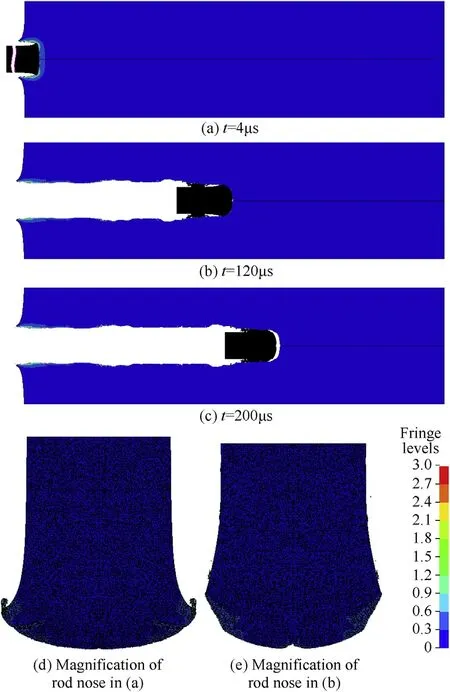
Fig.7.Evolution of effective strain in the rod and the target for the WHA rod penetration into 6061-T651 aluminum target at V0=1060 m/s.

Comparatively,regarding to the composite rod,as seen in Fig.8(d),in the early stage,though WPs also experience extreme plastic deformation and the rod nose displays a certain blunt deformation,how ever,the extent is remarkably low er compared w ith the deformation in the WHArod(see Fig.7(d)).Especially,due to the high shear sensitivity of the MGmatrix,shear bandsor cracks propagate speedily towards the back end after the nucleation in the front end,and at the same time they w ill impact onto the surrounding WPs during the propagation.Thus,the propagation distance of shear cracks is relatively long,and eventually they intersect w ith each other in the central axis of the rod.This leads to a coneshaped fragment in the front end,being similar to the cases of monolithic MG and the corresponding particle reinforced composite under the anvil-on-rod impact condition[16,30].

Subsequently,materials w ithin the cone-shaped fragment and in other zones of the rod nose fracture gradually along w ith the penetration process,and the rod nose becomes a f l atter shape again.During this erosion process,new shear cracks initiate again w ithin the rod nose,and cracks propagate obliquely towards the side surface from the central axis.When the shear cracks run through the rod,the front part begins to separate from the rod again,and then the nose becomes a sharp shape,as show n in Fig.8(e).At the same time,a new cone-shaped fragment is formed w ithin the sharp nose and it further separates out,thus the nose becomes f l atter again.Similarly,the sharpening behavior w ill occur once more in the nose because of the newly initiated shear cracks.During the latter penetration process,the rod w ill repeat this“sharpening-f l attening-sharpening”behavior until it stops eventually.Besides,it is w orth noting that in the w hole latter stage,there is almost no blunt deformation in the rod nose.

Similar to the case of a tungsten f i ber reinforced(WF/MG)composite rod[7-9],this separated part in the front end of the composite rod can be called“edge layer”.How ever,different from the edge layer in the WF/MG composite rod w ithin w hich the tungsten f i bers(WFs)are not completely cut off and they are still connected to the rod,the edge layer separates from the rear part of WP/MG composite rod completely,as seen in Fig.8(e),and materials w ithin the edge layer fracture severely.Hence,the mass erosion of the WP/MG composite rod during the“self-sharpening”process is much more remarkable compared w ith that of the WF/MG composite rod.

4.2.Variations of stress and rod velocity

Variation of stress in the rod w ill be analyzed f i rst,and the key points show n in Fig.2(a)are used for the corresponding discussion.Tw o penetrating cases in Tables 2 and i.e.,that under V0=998 m/s and 1060 m/s for tw o kindsof rods,are selected for comparison due to that the impact velocities are similar to each other.Fig.9 lists variations of effective stress in the key points for the tw o penetrating cases.

Regarding to the composite rod,because of the high strength and high shear sensitivity of MG material under the impact condition[9,27-30],the high-speed impact leads to the stress in the MG matrix w ithin the nose increasing speedily to an extremely high value(about 7.5 GPa).After yielding,the matrix softens precipitously and then fails immediately.For the surrounding WPs,the stress also increases speedily to the yielding point(about 2.1 GPa)after the impact.Due to the impact effect of shear bands or shear cracks from the MGmatrix,WPsfail immediately after the failure of the MG matrix.For the middle part of the rod,at the arrival of the impact stress w ave,the corresponding WPs yield at once and then they experience a certain duration of plastic deformation.Comparatively,regarding to the MGmatrix,the increase of stress is a little slow in the early stage,and subsequently it also reaches a high value,f i nally the stress further drops and the MGmatrix fails.This characteristic is mainly derived from the dependence of the strength of MG on the strain rate(see Appendix A and Table A1).Similarly,the surrounding WPs also fail immediately after the failure of the MG matrix.At the back end of the rod,because the back face is free,the stress is alw ays low during the w hole penetration.

Consequently,it is know n that,similar to the case for the WF/MG composite rod[9],the MG matrix can achieve a high strength before failure during the penetration process,and thus it can hold f i rmly the surrounding WPs.Comparatively,after the failure of the MG matrix,shear cracks propagate speedily in the rod nose and then the“edge layer”in the front end separates out from the rod.Hence,blunt deformation w ould not occur in the rod nose and the WP/MG composite rod displays a“self-sharpening”property.

Regarding to the WHA rod,though variations of stress are similar to that in WPs w ithin the composite rod,the rod deforms in a monolithic manner,and the corresponding failure of rod material is later compared w ith the failure of WPs in the composite rod.Consequently,the WHA rod can sustain a longer duration of plastic deformation,and f i nally it results in a“mushroom”rod nose.

Additionally,for the long rod penetration,another important parameter is the rod velocity(tail velocity)from w hich the resistance exerted on the rod can be inferred.Variations of rod velocity in different penetrating cases w ill be analyzed,and related simulation results are listed in Fig.10.It is found that because the rod is relatively short(38.1 mm),and the aspect ratio is small(L/d=6),the decrease of rod velocity during the penetration is faster than that of a relatively long rod(L=206 mm[9]),and it is similar to that of a small arms projectile(L=28.1 mm[37]).Besides,the decrease of velocity for the composite rod is slow er than that for the WHA rod,and correspondingly the composite rod achieves a deeper DOP.Likew ise,this is mainly due to the“self-sharpening”behavior of composite rod and the corresponding low resistance.

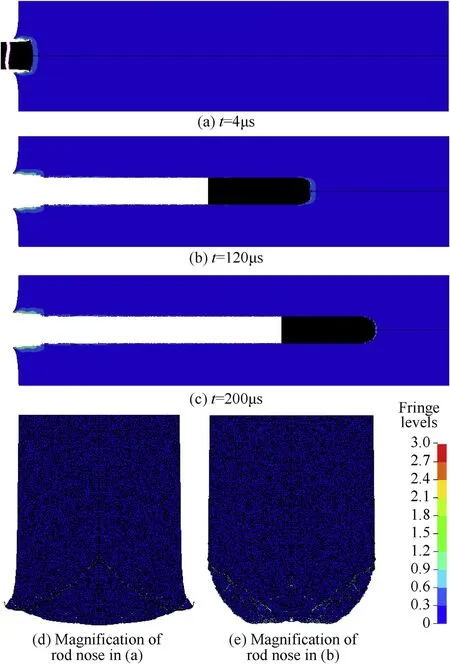
Fig.8.Evolution of effective strain in the rod and the target for the WP/MG composite rod penetration into 6061-T651 aluminum target at V0=998 m/s.

As the authors'previous w ork[9]demonstrated,regarding to the penetration of a composite rod,the sharpening behavior could induce a low resistance,how ever,at the same time the speedy separation of rod material from its nose w ill lead to considerable mass erosion.Besides,as mentioned in section 4.1 above,compared w ith the WF/MG composite rod,the edge layer of the WP/MG composite rod separates from its rear part completely.This leads to more remarkable mass loss and it w ill further w eaken its penetration performance.Choi-Yim et al.[6]'s test results also demonstrated that the penetrating capability of a WP/MG rod is a little low er than that of the WF/MG one.

5.In f l uences of different factors on the ballistic performance of com p osite rod

In f l uencesof different factorson the ballistic performance of the WP/MG composite rod w ill be further discussed.Similar to the analysis on the WF/MG composite rod penetration[9],three main factors,i.e.,impact velocity,target strength and initial nose shape,w ill be emphasized,and in related analysis Conner et al.[5]and Choi-Yim et al.[6]'s penetrating tests are also considered.

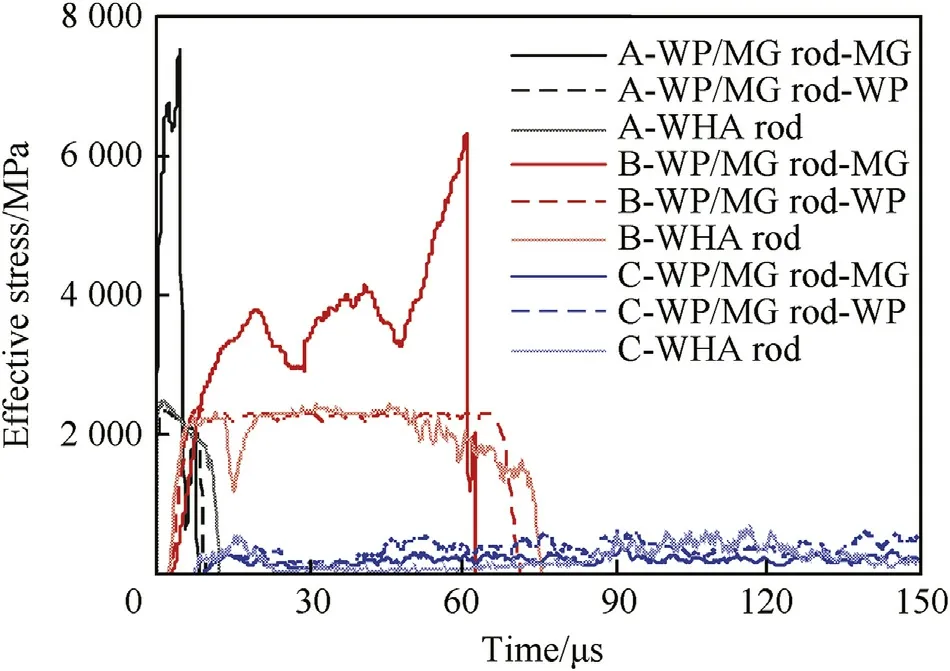
Fig.9.Variations of effective stress in the rods for the WHA rod penetration at V0=1060 m/s and the WP/MG composite rod penetration at V0=998 m/s.

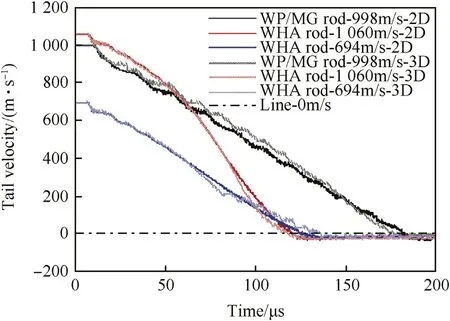
Fig.10.Variations of rod velocity for different penetrating conditions.

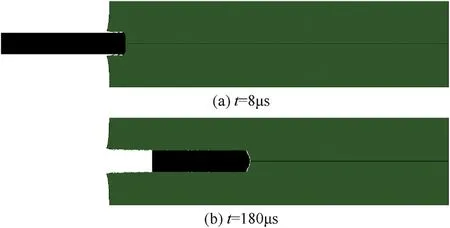
Fig.11.Deformation and failure process of rod and target under penetration into 6061-T651 aluminum target at V0=694 m/s.

5.1.Impact velocity

Discussions w ill consider both the low and high impact velocities.For the low velocity,V0=694 m/s in Conner et al.[5]'s test is selected,and a typical value of V0=1500 m/s is adopted to represent the high velocity.

Fig.11 lists the penetration process at V0=694 m/s.Because of the strain rate sensitivity(see Appendix A and Fig.9),the yielding stress of the MG matrix under this low impact velocity is much low er than that under the high velocity,and failure initiates immediately in the matrix after yielding.Consequently,the constraint effect provided by the MG matrix on the surrounding WPs is relatively w eak,and the impact of shear bands or cracks from the matrix on the WPs is not strong enough.How ever,shear cracks can still propagate along the edge of WPs,and then shear cracks run through the rod and induce the edge layer in the rod nose.This further leads to the separation of materials w ithin the edge layer from the long rod.Thus,there is still almost no blunt deformation in the nose.However,the mass loss of rod is severe,and correspondingly the DOP is relatively small,w ith a value of about 42 mm.

The corresponding penetration process at V0=1500 m/s is show n in Fig.12.It isseen that there isalmost no blunt deformation in the rod nose during the w hole penetration process.In the latter stage,a bulge is plugged on the back surface of the target,and the lateral squeeze action of the target on the rod nose becomes w eaker,nevertheless,blunt deformation still doesn't occur and the rod nose keeps the sharp shape(see Fig.12(b)).After the target is perforated,a cone-shaped penetrating hole is formed at the back end of the target.

Besides,the strain rate increases under the higher impact velocity,and correspondingly the strength of MGmaterial achieves an increment.Consequently,the constraint of the MG matrix on the surrounding WPs is more remarkable,and thus failure is harder to occur in the rod.The simulation results show that under V0=1500 m/s,the residual rod after perforation of the target is still relatively long,w ith a length of about 19.5 mm,being similar to that after a penetration w ith DOPof 86 mm at V0=998 m/s(19 mm,see Table 2).Thus,it can be inferred that under the higher impact velocity,the residual rod w ill keep higher velocity and larger mass after the target is perforated,and the corresponding destructive potency for the objects behind the target w ill achieve an improvement.

Moreover,the contour pro f i les of the penetrating hole w ithin the target under three different impact velocities are show n in Fig.13.Diameters of the penetrating hole are almost the same,and they are all close to that of the rod shank.This implies that corresponding to various impact velocities,blunt deformation w ould not occur in the nose of the WP/MG composite rod.

Fig.12.Deformation and failure process of rod and target under penetration into 6061-T651 aluminum target at V0=1500 m/s.

Hence,it can be know n that similar to the case of the WF/MG composite rod,a threshold impact velocity may exist for the effective penetration of the WP/MG composite rod.When the impact velocity is low,the MG matrix is hard to constrain f i rmly enough the surrounding WPs,and after the failure of the MGmatrix shear cracks propagate speedily along the edge of the WPs,and it leads to stripping out of the WPs.Thus,materials w ithin the rod nose fracture and the rod cannot penetrate effectively into the target.Comparatively,under the high impact velocity,the constraint of the MG matrix on the WPs is relatively strong,and thus the rod erosion w ill be reduced.At the same time,shear deformation and failure of materials ensures the rod behaves in a“self-sharpening”manner.Consequently,the corresponding penetrating capability of the composite rod is greater,and its residual rod w ill maintain better destructive potency.How ever,at any impact velocity,the mass erosion of the WP/MG composite rod is more severe than that of the WF/MG rod,and correspondingly its penetrating performance as w ell as the subsequent destructive potency is low er compared w ith that of the latter.

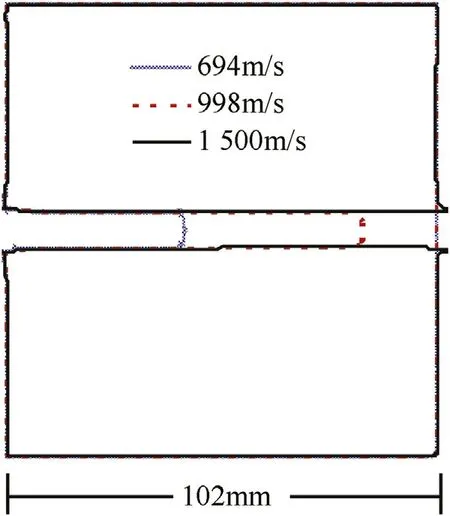
Fig.13.Contour pro f i les of penetrating hole in the 6061-T651 aluminum target under different impact velocities.

5.2.Target strength

During the penetration process,the rod w ill undergo resistance from the target,and the lateral squeeze of target material w ill induce separating out of materials from the rod nose.Correspondingly,a“self-sharpening”behavior occurs and at the same time there is signi f i cant mass erosion for the rod.The resistance and the lateral squeeze action from the target are related to the target strength,and the in f l uence of target strength on the ballistic performance of the WP/MG composite rod w ill be discussed as follow.For comparative analysis,tw o kinds of target materials in section 2,6061-T651 aluminum and 30Cr Mn Mo steel(w ith much higher strength),are selected for related discussions.

Fig.14 lists the contour pro f i les of the penetrating hole in different targets under the three impact velocities.At V0=694 m/s,the rod can't penetrate effectively into the steel target.Consequently,it can be inferred that the threshold impact velocity for effective penetration w ill be higher corresponding to the higher target strength.Regarding to the cases of V0=998 m/s and V0=1500 m/s,the DOP in the steel target is also signi f i cantly smaller than that in the aluminum one.This is ascribed to that the strength of steel is higher and its plasticity is better(see Table 1),and thus its squeeze action on the rod nose is more remarkable.Consequently,corresponding to the steel target,the rod nose is easier to fracture,i.e.,the mass erosion of the rod is more severe.The simulation resultsshow that the length of the residual rod after penetration into the steel target under the above three impact velocities is 13.5 mm,10 mm and 4.5 mm,respectively,being signi f i cantly less than those for the aluminum target(see Table 2 and analysis in section 5.1).

Besides,compared w ith the case of the WF/MGrod(see Ref.[9]),the penetrating capability of the WP/MGrod into the steel target is also less,and Choi-Yim et al.[6]'s penetrating tests regarding to the 4130 steel target also demonstrated such a feature.The main reason is that mass loss in the nose of the WP/MGrod is more remarkable.As the analysis in section 4.1 demonstrates,the edge layer of the WP/MG rod separates from the rod early,comparatively,for the WF/MG rod,though materials w ithin the edge layer experience extreme deformation,the edge layer is still connected to the rear part of the rod,and thus its mass erosion is slow er.

Fig.15 further show s the corresponding variations of rod velocity in different impact cases.The decrease of velocity is remarkably faster corresponding to the steel target,and the rod stops after only a short duration.Comparatively,regarding to the aluminum target,the decrease of rod velocity is much slow er,and for the case of V0=1500 m/s it maintains as constant after the target is perforated.Related deviation is mainly derived from that the total resistance acted by the steel target is larger,and it leads to more severe fracture of the WP/MG composite rod.

5.3.Initial nose shape

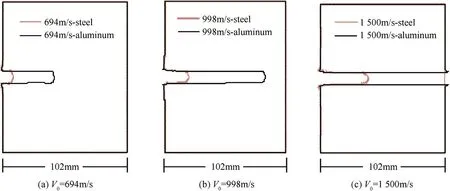
Fig.14.Contour pro f i les of penetrating hole in different targets under various impact velocities.

The authors'previous investigations demonstrated that different nose shapes of the rigid long rod w ill lead to signi f i cantly different penetrating resistance as w ell as the consequent DOP[38,39];Comparatively,for the penetration of the WF/MG composite rod,the rod nose sharpens immediately after a short duration,and the effect of the initial nose shape on the f i nal DOP is insigni f i cant[9].Similarly,the corresponding in f l uence on the ballistic performance of the WP/MG composite rod w ill also be analyzed.

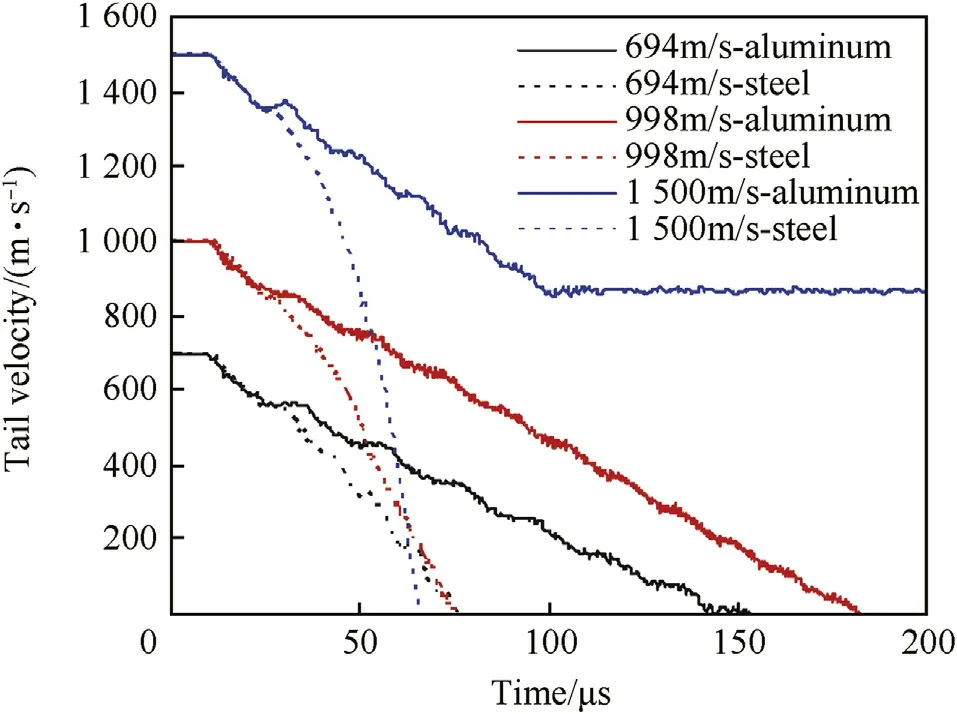
Fig.15.Variations of rod velocity for different penetrating conditions.

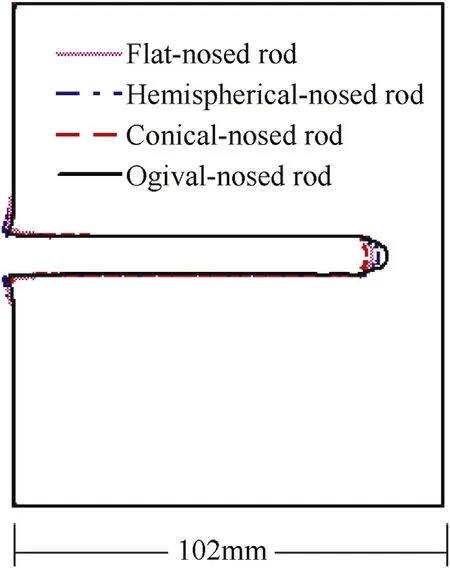
Fig.17.Contour pro f i les of penetrating hole for the rods with different initial nose shapes.

Likew ise,four nose shapes w ith different sharpness levels,i.e.,the ogival nose w ith a caliber-radius-head(CRH)ofψ=1.5,the conical nose w ith a half apex angle ofθ=45°,the hemispherical nose and the f l at nose,are selected for comparison.All rods are set as the same length(38.1 mm)and the same shank diameter(6.35 mm)as the composite rod in Choi-Yim et al.[6]’test(see Fig.2).For convenience of comparative analysis w ith the corresponding test data,the target material is still de f i ned as 6061-T651 aluminum,and the impact velocity is determined as V0=998 m/s.

Related simulation results show that for all the four kindsof rods self-sharpening behavior initiates after only a short duration of impact,and then materials w ithin the rod nose separate out.Thus,blunt deformation does not occur in all rods until they stop f i nally.Fig.16 lists the corresponding residual rods,and it is seen that all the noses sharpen as a sharp shape eventually,and their length is similar.Fig.17 further show s the contour pro f i les of penetrating hole for the four kindsof rods,w hich show sthat both the diameters of penetrating hole and the DOPs are almost the same for different cases,and the mechanism for the small deviation among different nose shapes can be seen in our previous investigation on the WF/MGrod[9].Additionally,the evolutions of rod velocity are listed in Fig.18,from w hich it can be found that they are also similar w ith each other.

Fig.16.Residual rods after penetration for rods w ith different initial nose shapes.

Hence,it is know n that the in f l uence of the initial nose shape on the“self-sharpening”behavior as w ell as the corresponding penetration performance of the WP/MG composite rod is insignificant.In the practical application,a hemispherical nose could induce more appropriate lateral squeeze from the target in the initial penetrating stage,and thus the propagation of shear cracks w ithin the rod nose could be delayed.Besides,it is also bene f i cial to a high enough structural rigidity.

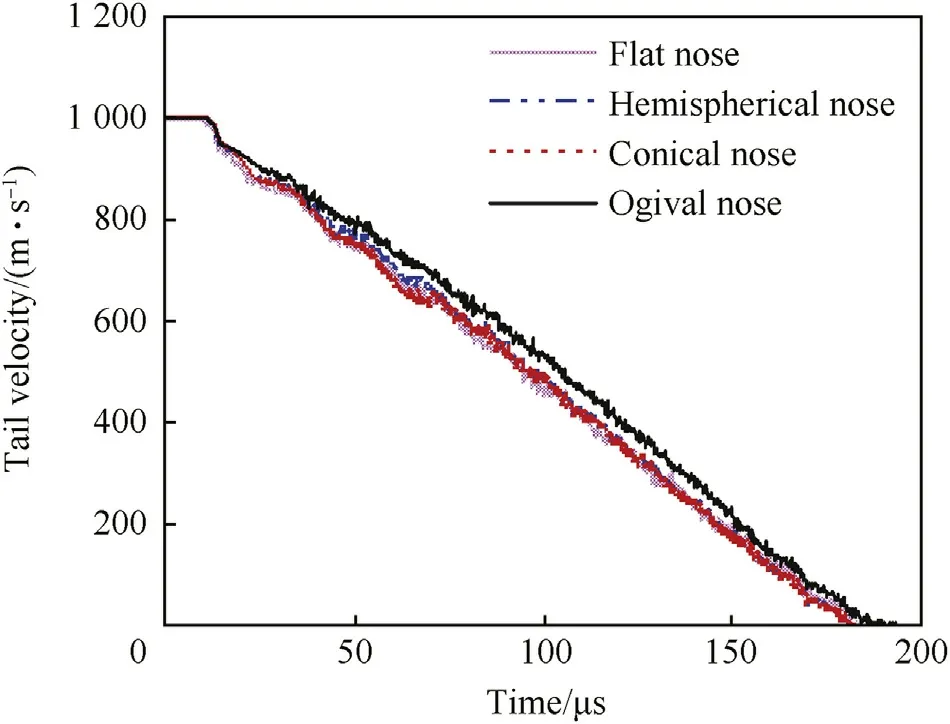
Fig.18.Variations of rod velocity for the rods w ith different initial nose shapes.

6.Conclusions

FEM numerical analysis on the ballistic performance of a WP/MG composite rod is performed,and comparison among the penetrations of the WHA rod,the WF/MG composite rod and the WP/MG composite rod is conducted.In the simulations a modi f i ed coupled thermo-mechanical constitutive model is employed to describe the mechanical property of the MG matrix,and geometrical models of the composite rod are established based on itsinner structure.Thus the numerical simulations depict relatively w ell the ballistic performance of the composite rod,and they can provide good reference signi f i cance to the practical engineering.Moreover,in f l uences of various factors,including the impact velocity,the target strength and the initial nose shape,on the ballistic performance of the WP/MG rod are further discussed.

Related analysis show s that due to the high plasticity of the WHA material,the WHA rod nose becomes blunt and forms a“mushroom”shape during the penetration.Comparatively,the WP/MG composite rod displays a“self-sharpening”behavior,and an“edge layer”is formed in the rod nose.How ever,different from the case of the WF/MG composite rod,the edge layer in the WP/MG composite rod separates completely from its rear part,and materials w ithin the edge layer fracture severely due to the squeeze of target material.Thus,mass erosion of the WP/MGcomposite rod is more remarkable compared w ith that of the WF/MG one.Consequently,the penetrating capability of the WP/MGcomposite rod is better than that of the WHA rod,but it is less than that of the WF/MG one.

The impact velocity and the target strength have signi f i cant in f l uences on the ballistic performance of the WP/MG composite rod.When the impact velocity is low,the composite rod can't penetrate effectively into the target.Comparatively,under the high impact velocity,the penetrating capability of the rod and the subsequent destructive potency of its residual rod w ill increase considerably w ith increasing the impact velocity.Besides,failure of materials w ithin the rod nose is more severe corresponding to the higher target strength,and the decrease of its penetrating capability compared w ith that of the WF/MG composite rod is more remarkable.How ever,the effect of initial nose shape is insigni f i cant.

Acknow ledgements

The project is supported by the Science and Technology Development Fund(2015B0201025)as w ell as the key subject“Computational Solid Mechanics”of China Academy of Engineering Physics,the National Outstanding Young Scientists Foundation of China(11225213)and the National Natural Science Foundation of China(11521062,11602258).

Appendix A.Modi f i ed coupled thermo-mechanical constitutive m odel for m etallic glass

By considering all the effects of free volume,temperature and hydrostatic stress on the deformation and failure of metallic glass(MG),a modi f i ed coupled thermo-mechanical constitutive model can be obtained as[29,30]In Eq.(A1-A3),a dot over a quantity（）denotes the differentiation w ith respect to time.

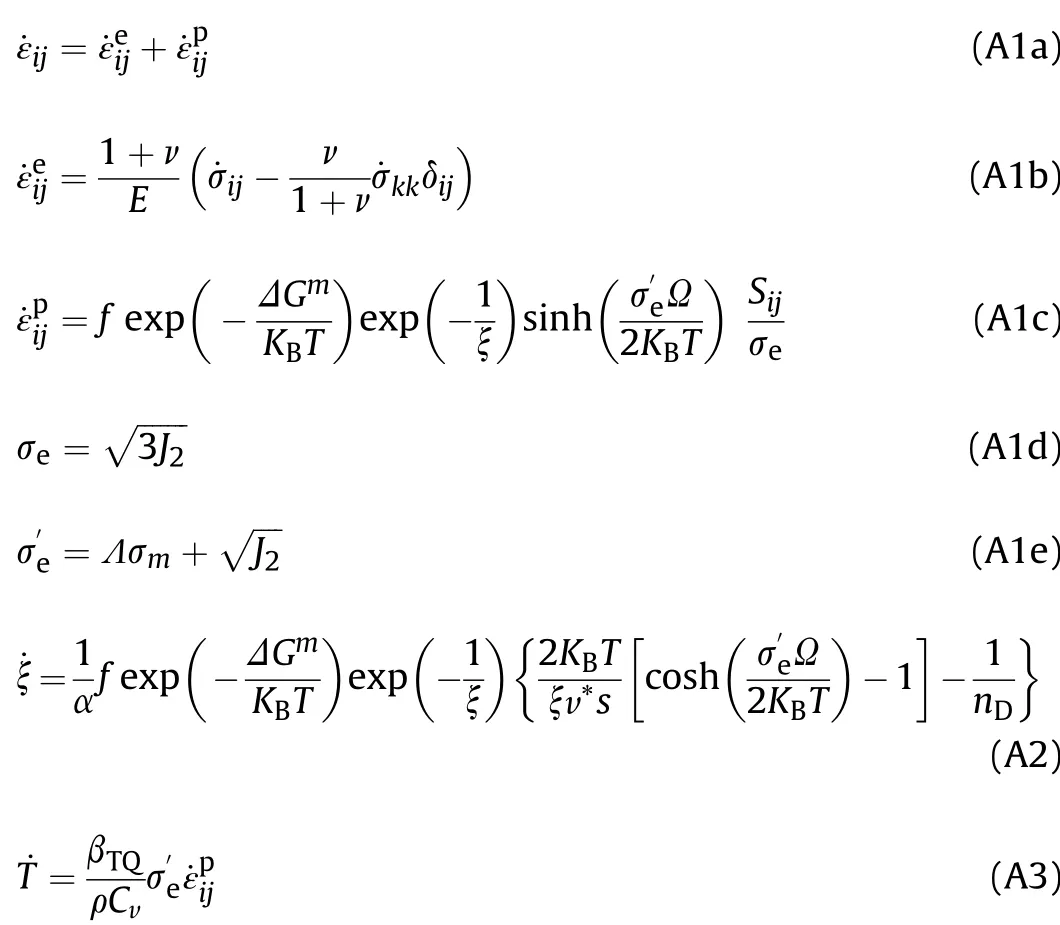
In Eq.(A1)E andνare the Young's modulus and Poisson's ratio,respectively f is the frequency of atomic vibration;ΔGmis the activation energy KBis the Boltzmann constant and T the absolute temperatureξ=is the free volume concentration in MG(here

vf,v*andαare,respectively,the average free volume per atom,critical volume and a geometrical factorΩis the average atomic volumeσeis the von-Mises effective stress,in w hich J2=SijSij/2 is the J2invariant of stress Sij=σij-δijσmis the deviatoric stress tensor andσm=σkk/3 the mean stressσ′eis an effective stress w hich considers the contribution of hydrostatic stress,in w hichΛis the hydrostatic stress sensitivity factor,and its value varies w ith the stress statei.e.,the value ofΛCunder compression is different from that ofΛTunder tension

Eq.(A2)is the free volume evolution equation,in w hich s=E/［3（1-ν）］is the Eshelby modulus and nDthe number of diffusive jumps necessary to annihilate a free volume as v*.

Eq.(A3)is the temperature evolution equation,w hereρand Cvare the density and the speci f i c heat at constant volume,respectivelyεpe=

is the effective plastic strainβTQis the Taylor-Quinney coef f i cient and considered to be a function of the effective plastic strain rate

Furthermore,w hen the net free volumes exceed a critical value,failure occurs in the MG material,and thus the corresponding failure criterion is de f i ned as that the free volume concentrationξ exceeds the critical valueξc:

Appendix B.Johnson-Cook constitutive m odel and cumulative dam age failure criterion for m etals

The corresponding expression of Johnson-Cook model is[33].

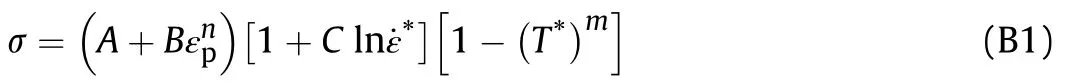
w here A,B,C,n and m are the material constants.A represents the yield stress at the reference strain rate(˙ε*=1),B and n represent the effect of strain hardening,C is the strain rate constant and m characterizes the thermal softening.˙ε*=˙εp/˙ε0is the dimensionless plastic strain,in w hich˙ε0is the reference strain rate and usually takes a value of 1s-1.T*=（T-Tr）/（Tm-Tr）is the homologous temperature,w herein Tmis the melting temperature,Tris the reference temperature and usually taken as the room temperature.

The temperature rise in the material is derived from the deformation energy,and the corresponding equation is

In the calculation it is usually assumed as the adiabatic deformation,and the value of Taylor-Quinney coef f i cientβTQin Eq.(B2)is taken as 0.9.

In the cumulative damage failure criterion a degree of damage D,is de f i ned to represent the failure of the material,and the corresponding expression is[34].

The value of D ranges from 0-1.When there is no deformation in the material,D=0.Comparatively,w hen the damage parameter increases up to its critical value,i.e.,D=1,fracture occurs in the material and the stress decreases to zero.In Eq.(B3)Δεpis the increase of effective plastic strain in a time step,andεfis the critical strain at failure of material w ith an expression of

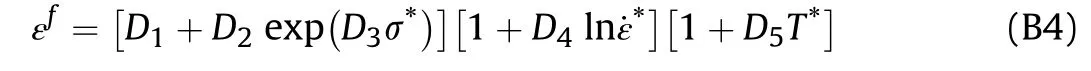
In Eq.(B4)σ*=P/σeis the ratio of pressure divided by the effective stress,in w hich P is the pressure.The parameters of D1-D5are the material constants.

Appendix C.Gruneisen equation of state

The Gruneisen equation of state de f i nes the pressure for the compressed material as[35].

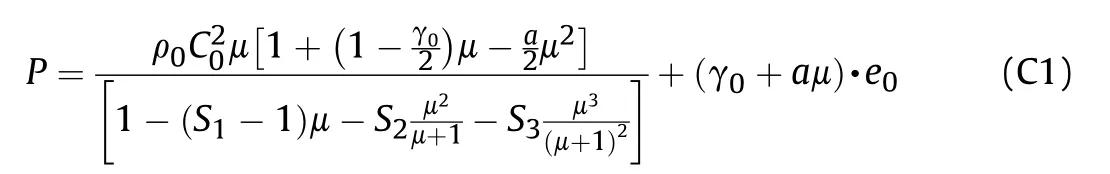
w here e0is the initial internal energy in the material;C0is the intercept of the vs-vpcurve;S1-S3are the coef f i cients of slope of the vs-vpcurve;vsis the shock w ave velocity and vpthe particle velocity;γ0is the Gruneisen coef f i cient;a is the f i rst order volume correction toγ0;μ=ρ/ρ0-1,in w hichρis the current density and ρ0the initial density.