基于树形马氏链模型的可靠性分析方法
张洪铭,顾晓辉,*,邸忆,2
1. 南京理工大学 机械工程学院,南京 210094 2. 武昌理工学院 信息工程学院,武汉 430223
工程实践中的系统可靠性分析过程具有设计变量多、低失效率和极限状态函数形式复杂甚至隐式的特点。失效概率(Failure Probability)Pf的准确计算是机械、电子系统可靠性分析的关键,Pf的本质是设计变量的联合概率密度函数在失效区域上的积分:
(1)
式中:X为各设计变量x构成的基本随机向量;G(x)为系统的极限状态函数(Limit State Function,LSF),G(x)≤0表征失效区域;fX(x)为设计变量的联合概率密度函数。前述工程实践问题的特点使得直接处理式(1)的难度极大,难以直接积分获得精确的系统失效概率,因此针对强非线性问题的高效模型是目前工程可靠性分析研究的关键。
目前的4类系统可靠性分析方法[1]中,以蒙特卡罗模拟(Monte Carlo Simulation, MCS)为基础的数字模拟算法原理简洁、适应性强,对问题的维度不敏感,适合用于处理考虑不确定性的系统可靠性分析问题。进一步地,针对原始MCS方法在实际应用中效率低下的问题,重要抽样(Importance Sampling,IS)法[2-3]利用方便采样的重要抽样分布,在靠近失效域边界的设计点处进行抽样,使得对失效概率贡献大的区域内的样本有较大概率被抽到,增大失效样本的比重从而提升抽样效率。确定设计点位置和构造最优的重要抽样分布是提升IS算法性能的关键,为此学者们进行了广泛的研究。马纪明等[4]提出的条件递归方法能在系统的LSF为隐式时快速找到设计点;为了避免重要抽样分布的抽样中心落入局部最优区域,文献[5]借助模拟退火算法寻找全局最优设计点。上述文献中较少提及重要抽样分布的构造过程,实际上,不合适的重要抽样分布容易导致估计结果的方差很大[6]。为了避免因主观选择重要抽样分布类型而导致的算法性能下降,同时减少寻找设计点的计算开销,自适应重要抽样法应运而生。侯本伟等[7]采用基于演化过程和交叉熵模型的多准则迭代方法来计算重要抽样函数,使预抽样次数下降为原来的1/40;陈向前等[8]提出的主动导引技术,使抽样中心能快速自适应地逼近设计点;唐承等[9]提出的粒子群序列二次规划混合算法有较强的全局搜索能力;Au和Beck[10]将马尔可夫链与IS算法结合,构造收敛规则,使马氏链收敛后的稳定分布与最优重要抽样分布相同或近似,用收敛后的状态点进行核密度估计从而得到最优的重要抽样分布密度函数。该方法中马氏链的收敛过程即是状态点在失效域中的自适应探索过程,适用于失效域形状复杂的情况。戴鸿哲等在Au工作的基础上进行了深入研究,其先在文献[11]中借助快速高斯变换大幅降低核密度估计的计算复杂度,有效缩短了计算耗时;而后在文献[12]中以马氏链收敛后的状态点作为支持向量机的数据样本,拟合出近似极限状态函数,有效解决了失效域复杂、极限状态函数隐式条件下的可靠性计算问题。
在前述可靠性分析研究的基础上,为了进一步提高处理强非线性问题的效率,提出了基于树形马氏链重要抽样(Tree Markov Chain Importance Sampling, TMCIS)模型的系统可靠性分析方法。文中提出的树形马尔可夫链算法是对原始马氏链的改进,新的抽样机制使其具有局部多链并行和自适应样本转移的特性,能够从抽样起点自动向失效域边界搜索,并在关键样本密集区域内灵活地生成支链来提升抽样效率。由树形马氏链生成的样本,能够最大程度地反映出失效分布的特征信息,使得核密度估计的结果能最大程度地近似于真实失效分布。文末给出了2个强非线性数值算例和BAT子弹药弹翼的工程算例,计算结果显示本文提出的算法在提高抽样效率及计算结果准确度的同时具有较好的稳定性。
1 树形马氏链模型
1.1 Metropolis-Hasting算法
满足了细致平稳条件(Detailed-balance Condition)的非周期马氏链会收敛到一个平稳分布,分布形式与转移矩阵或转移函数有关。MCMC(Markov Chain Monte Carlo)方法利用了马氏链的这一特性,即通过构造马氏链的转移矩阵或函数,使得链的平稳分布类型为目标分布类型或与目标分布类型十分近似,则马氏链收敛后的状态点即可看作从目标分布中抽得的样本点。M-H算法(Metropolis-Hasting Method)[13]是MCMC方法的常见形式,其算法步骤为
步骤1给定马氏链的初始状态X0=x0,其中x0∈R,初始化计数变量t、设置总样本点数N,这里的t,N∈N。
步骤2对t=1,2,…,N循环以下过程进行采样:
1)第t次抽样,马氏链状态为Xt=xt,依建议分布产生候选点y~q(x|xt),
2)从均匀分布抽得一个随机数:u~U(0,1),计算步骤1)中候选点y的接受率:
(2)
式中:p(·)为先验分布;q(·|·)为建议分布;α为接受率。
3)如果α(xt,y)>u,则接受转移,令xt+1=y;否则拒绝y,令xt+1=xt。
分析上述算法,在马氏链满足细致平稳条件的前提下,若建议分布为对称分布,亦即q(xt|y)=q(y|xt),则式(2)中的接受率可以进一步写为:α(xt|y)=min{1,p(y)/p(xt)},可见当候选点处的目标分布概率密度越大时,候选点越容易被选中;同时,接受率的形式保证了概率密度较小的样本点也有被选中的可能,从而防止马氏链“陷入”目标分布密度函数的局部峰值区域,这增强了算法对状态空间的遍历性能,使抽到的样本点更加贴合目标分布的分布特点。
原始M-H算法由于引入了马氏链,使得抽样过程具有自适应特性,但当状态空间维度较高时,概率密度稀疏处的样本很容易被拒绝,且M-H算法每次只决定一个点被接受与否,使抽样效率很低;同时,马氏链中相邻状态的产生方式决定了相邻样本点间是相关的,为了满足样本的独立性要求,普遍的做法是从已经收敛的马氏链中,每隔r个点选取一个点形成新的链,若总样本点数为N,则原始马氏链的抽样次数至少应为[N(r+1)-r],即原始马氏链的抽样次数会成倍增长,需要更多的时间和计算成本来完成抽样,导致抽样效率进一步下降。
1.2 树形马氏链算法
针对上述不足,树形马氏链算法充分利用相邻状态点间的关系信息,对单次抽样步的候选点数量进行合理扩充,允许当前状态点可以产生多个候选点,使得单次抽样步中被接受候选点的数量的平均值大于1。树形马氏链的抽样机制,使得抽样结果在生成关系上呈现出以抽样起点为根节点的“树状”结构,有效样本密集的区域会有多个候选点被接受为样本点,这是树结构中产生“枝杈”的直接原因。树形马氏链中的支链增强了算法对设计域充分搜索的能力,提高了抽样效率。为了完整、充分地表达算法内容,提出了基本向量和跳转向量的概念来实现树形马氏链算法模型的抽样机制,概念的具体定义为:
定义1(基本向量) 指马氏链的当前状态点依据建议分布产生候选点(该候选点称为基本候选点)后,由当前状态点指向基本候选点的向量。
定义2(跳转向量) 由基本向量在状态空间中经过若干次变换后得到的向量。跳转向量必须以当前状态点为起点,则其末端指向的点称为扩充候选点,跳转向量与基本向量的L2范数相等。

给出树形马氏链抽样步骤如下:

步骤2在当前样本量的值小于N时,令t=1,2,…;循环下列步骤采样:

2)依据步骤1)中产生的成对父子点对,计算父点的基本向量:
(3)

3)计算每个候选点的接受率:
(4)

树形马氏链算法对由基本向量生成跳转向量的具体实现方法不做强制要求(满足定义2的内容即可),以适应不同实际情况下的具体问题。本文给出了设计变量为二维随机变量时,采用快速生成跳转向量并得到候选点的方法。基本向量的旋转动作依靠变换矩阵实现,二维时的变换矩阵为
(5)
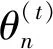
(6)
图1为设计变量为二维时,树形马氏链抽样机制示意图,图中2条极限状态函数曲线将设计域分割成4个区域,左下方区域为非失效区域,候选点的产生、接受或拒绝状态如图所示;图1中的抽样过程所得的点按照生成关系和接受、拒绝状态可以表达成图2所示的树形结构,这是树形马氏链算法的命名由来。

图1 TMC抽样机制Fig.1 Mechanism of TMC sampling

图2 TMC样本数据结构Fig.2 Data structure of TMC samples
2 核密度估计
2.1 重要抽样法
原始IS算法是对MCS的改进,是一种典型的方差缩减技术。MCS算法的抽样中心在远离失效域边界的均值点处,在低失效率问题下MCS算法抽到失效样本的概率很小,因而需要大量抽样次数才能有少数失效样本被抽中。为了减少抽样次数,IS算法利用测度变换增大极限事件的发生概率,亦即使对失效率贡献大的区域以较大概率被抽中。设计点是失效域附近密度函数值最大的点,因此IS算法选择设计点为抽样中心来提高抽样效率。基于上述IS方法的原理,可将式(1)中失效概率的积分区域从失效域改写到整个设计空间:
(7)
式中:Θ∈RN为设计空间;IG(x)为示性函数,表征样本是否在失效域中;当G(x)≤0时,有IG(x)=1;当G(x)>0时,IG(x)=0。引入的hX(x)是关于随机变量的重要抽样密度函数,hX(x)需要满足归一性、非负性且其分布类型应当便于采样。考虑式(7)的统计意义可以得到失效概率的期望为
(8)


表明重要抽样法求得的失效概率的估计值为无偏估计,此处可得最优重要抽样分布为
(9)

(10)
由于样本方差依概率收敛于母体方差,即有
(11)
(12)
2.2 重要抽样分布的核密度估计
使用树形马氏链抽样得到表征失效域的样本点之后,需要通过样本点得到重要抽样分布,本文采用描述能力较强的自适应核密度估计(Kernel Density Estimation, KDE)算法,来构建重要抽样分布密度函数。核密度估计[14-15]的本质是用一系列核概率密度函数的组合来产生合适的目标分布,形式为[16]
(13)
式中:θ(j)(j=1,2,…,M)为树形马氏链生成的样本点;这里的n为设计变量的维数;ω为窗口宽度;λi为局部带宽因子,用来调整窗口宽度的值;K(·)为核概率密度函数,通常取正态分布类型。
窗口宽度参数ω的本质是各个核概率密度函数进行组合时的权重,其决定了最终的核函数的平滑性。过大的ω值会使核函数过于“光滑”而丢失局部特性;过小的ω值会导致核函数尾部因为叠加效应而产生波动(或称为噪声)。文献[17]中给出了较好的值选择:
(14)
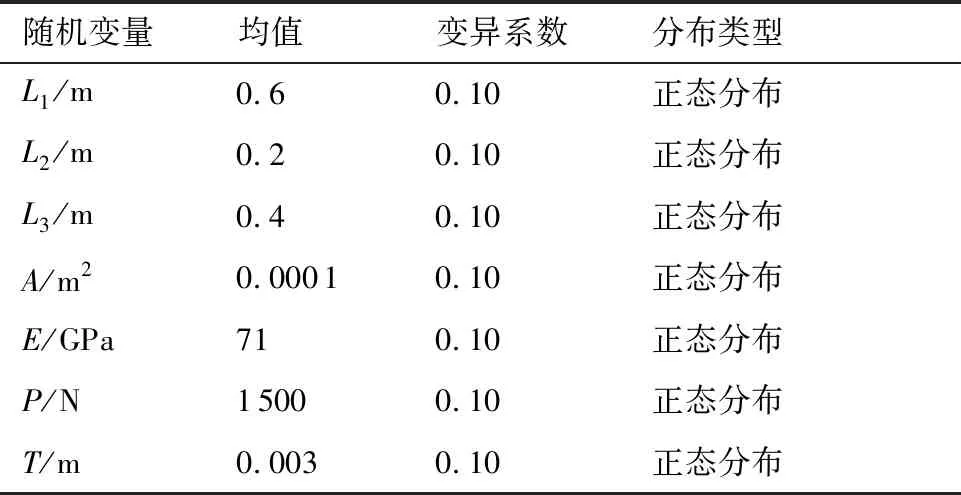
式中:Md为不同样本的个数(Md (15) 式中:α∈[0,1],通常取α=0.5[18];当α=0时,自适应核密度估计变为固定窗口宽度核密度估计。 提出了基于TMCIS模型的系统可靠性分析方法,分析流程如图3所示。其基本思想是:通过树形马氏链,快速生成尽可能服从真实目标分布的随机样本后,对这些样本进行核密度估计得到重要抽样分布函数,从获得的分布函数进行抽样,得到随机的设计状态样本,判断每个样本下系统对应的工作状态,来评估系统的失效概率并计算该次评估的方差。 图3 TMCIS可靠性分析方法流程Fig.3 Flowchart of TMCIS reliability analysis method 本节通过2个数值算例和1个工程算例,对所提算法的适应性、计算效率和准确度进行检验。选用了其他算法与本文方法进行对比分析,其中包括:原始蒙特卡罗(MC)算法、一次二阶矩法(FOSM)及改进一次二阶矩法(AFOSM)、原始重要抽样法(IS)、Metropolis-Hasting算法(M-H)。各算例结果如表1所示,N为各方法的样本总量和TMCIS方法中树形马氏链的抽样数,M为TM-CIS方法的重要抽样数;表中数据除AFOSM的 表1 算例1各方法计算结果Table 1 Calculation results of methods in Example 1 结果为公式推导所得,其余均为50次计算结果均值。本文提出的TMCIS方法在各算例中均使用高斯核进行自适应核密度估计。 算例1选取非线性程度较强的LSF检验TMCIS方法对强非线性多维问题的处理能力。所选极限状态函数为 g(θ)=3-Y+(4X)4 (16) 这里θ=(X,Y)为随机向量,2个随机变量X、Y独立同分布且均服从标准正态分布,系统有一个设计点位于(0,3)处。TMC算法中m=4,跳转向量采用1.2节中变换矩阵法生成。TMCIS模型对本例抽样结果如图4所示,样本点自适应地从起点转移至设计点周围,图中带数字标签的等高线为KDE方法得到的重要抽样分布(重要抽样样本量与TMC样本量皆为800),KDE样本为该分布生成的重要抽样样本。 本算例使用了4种方法分别进行了计算,结果如表1所列,以MC算法的失效率估计值作为准确解,其中ε是其他3种算法计算结果与准确解间的相对误差,CALL为调用极限状态函数的次数。 图4 算例1的抽样结果Fig.4 Sampling results of Example 1 表1数据表明TMCIS算法在少样本量下计算结果的相对误差是AFOSM算法的1/5,这是由于AFOSM算法本质上是将非线性LSF在设计点处进行泰勒级数展开,仅取线性部分来近似计算失效概率。因此,当LSF的非线性程度较高时,AFOSM算法会产生较大误差,而TMC的抽样机制使得其抽得的样本尽可能地反映LSF的非线性信息,因此,相较而言TMCIS算法更适合处理非线性问题且能够在较少的样本量下得到较高准确度的计算结果。 算例2某串联系统[10]的极限状态函数为 g(x)=min(g1,g2) (17) 式中:串联的2个子系统极限状态函数分别为 表2中给出了上述各算法在不同样本量时的计算结果,图6反映了表2中计算结果随样本量的变化规律。图6中水平虚线处的纵坐标为Pf的精确值,虚线上下两侧的点线分别是误差为±5%的位置,从图中可以看出算法的准确度和稳定性方面TMCIS算法最佳,IS算法次之,MC算法最差。并且TMCIS算法相较于IS算法在样本量较小时即可得到高准确度的结果。另外,从表2中可以发现当N/M的值接近1且N+M的值在800~10 000之间时TMCIS算法性能最优。 图5 不同方法抽样的结果Fig.5 Sampling results by different methods 表2 不同样本量下3种算法计算失效概率结果Table 2 Calculation results of failure probability by three methods under different sample sizes 算法Pf/10-5(Cov)N/104=0.020.040.080.10.20.40.81MC7.90 (0.21)7.50 (0.30)IS7.69 (0.37)5.87 (0.24)6.81 (0.21)6.50 (0.19)6.72 (0.11)7.04 (0.17)6.83 (0.23)6.59 (0.18)TMCIS(M=800)6.84(M=200)6.70 (0.24)6.77 (0.11)6.73 (0.23)6.96 (0.12)6.79 (0.34)7.21 (0.19)6.98 (0.25)算法Pf/10-5N/104=24810204080100MC7.95(0.19)7.76(0.12)7.22(0.25)7.29(0.16)7.05(0.21)7.15(0.22)7.23(0.15)6.97(0.14)IS6.82(0.09)6.80(0.13)6.79(0.14)TMCIS(M=800)6.95(0.17)6.90(0.23)7.02(0.22) 图6 3种方法计算结果随样本量的变化趋势Fig.6 Variation of calculation results with sample sizes of three methods 算例3BAT子弹药(Brainpower Anti-Tank submunition)是一种智能的末制导反坦克弹药,采用声波/毫米波复合导引手段来追踪、定位目标[19]。BAT子弹药的弹体中部有4个与弹体纵轴垂直、呈十字形分布的弹翼,4片弹翼的末端安装了声信号传感器,形成一个平面四元声传感器阵列,如图7所示。 由于要保证传感器阵列的测量精度,则各传感器之间的相对距离应保持在误差范围内。为了满足减轻总重和传感器布线的要求,弹翼框架的主体结构为由28根杆件和16片板壳刚性连接构成的三段盒式结构[20]。所有杆件的横截面积A相同,T为板的厚度;以L1、L2、L3分别表示X、Y、Z方向上杆的长度;杆和板的弹性模量为E,泊松比为常量取0.3;P为加在节点上的外载荷。翼盒结构和外载荷加载如图8所示。 图7 BAT子弹药外观结构Fig.7 Structure appearance of BAT submunition 取L1、L2、L3、A、E、P、T为随机变量,各随机变量的分布类型和分布参数如表3所列。距离声传感器最近的16号节点在Y方向上的最大允许位移为4.5 mm,以16号节点的Y向位移建立极限状态函数: g(X)16#,Y=[δ]-δmax(X) (18) 式中:X为由各随机变量构成的随机向量,即有:X=[L1,L2,L3,A,E,P,T]T;δmax(X)为各基本随机变量为X状态时16号节点的最大位移;TMC算法的m=8,8个子点中包含一个基本候选点和7个扩充候选点。不同于算例1、2使用变 图8 翼盒结构及外在加载示意图Fig.8 Schematic of wing box structure and external loading 表3 翼盒结构随机变量分布信息 Table 3 Random variable distribution information of wing box structure 随机变量均值变异系数分布类型L1/m0.60.10正态分布L2/m0.20.10正态分布L3/m0.40.10正态分布A/m20.00010.10正态分布E/GPa710.10正态分布P/N15000.10正态分布T/m0.0030.10正态分布 换矩阵生成跳转向量,本算例依靠基本向量的坐标轮转生成跳转向量。坐标轮转矩阵为 7个跳转向量依下列递推式生成: 表4中给出了各方法的失效概率计算结果[21]以及算得该结果所用的样本点数。从表中数据可以看出对非线性部分忽略最严重的AFOSM算法的计算结果误差最大。文中提出的TMCIS算法相较于文献[22]的算法和MCS算法,用更少的样本点数得到了相对准确的结果。 表4 算例3失效概率计算结果[22] 1) 文中通过分析算法原理,指出了FOSM算法及AFOSM算法处理强非线性问题时误差大的根源,同时针对原始MCMC算法单次迭代中,仅抉择一个候选状态接受与否带来的效率问题,提出了TMCIS模型。TMCIS的多候选点抽样机制保证了模型抽得的样本能充分自适应地探索设计域,在失效概率密度大的区域进行局部多链并行抽样,使得模型搜索效率提高的同时加快收敛速度。 2) 为了提高模型的稳定性、鲁棒性以更加适应带有强非线性特点的工程问题,TMCIS模型将TMC抽样算法与自适应核密估计结合,使得到的重要抽样分布与真实失效分布达到最大程度的近似。文末算例显示出了所提算法在不同样本量下,对超低失效率、串联系统问题的计算结果均能收敛到真值的范围内,验证了TMCIS算法的稳定性和可信度。 3) TMC抽样算法作为TMCIS模型的核心部分,其所具有的多候选状态抽样机制,在提高遍历性能以解决非线性问题的同时,能够进一步利用多个候选状态中携带的额外失效域信息,使得核密度估计的结果更加接近真实失效分布。这是文中所列算例中基于TMCIS模型的可靠性分析方法能以较少的样本点得到准确失效率的原因。2.3 TMCIS可靠性分析方法流程

3 算例分析





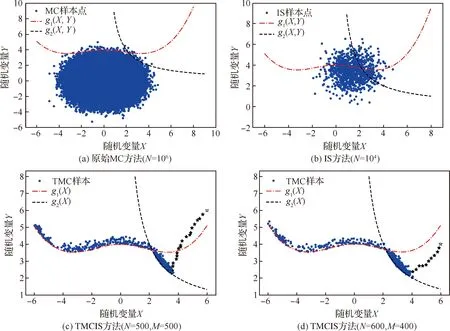

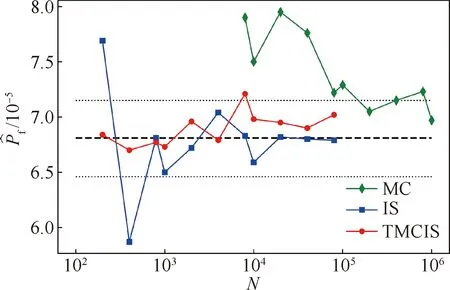

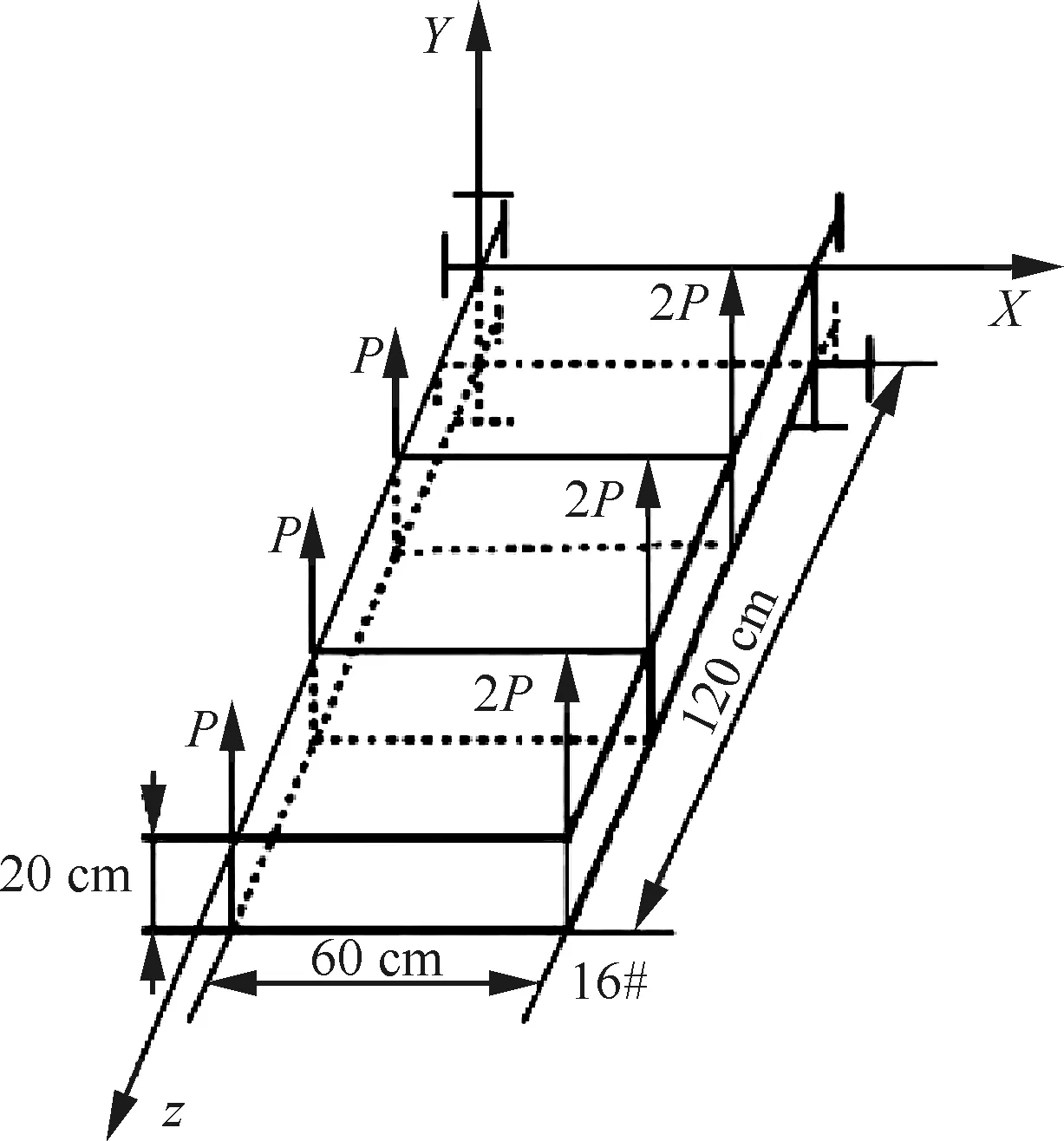


4 结 论

