非线性谐波法的轴向VNT涡轮内流场分析

张卫波， 杨际福， 王宝丰

(福州大学机械工程及自动化学院， 福建 福州 350108)

0 引言

增压器内部流场分析多采用定常流动的计算方法[1-2]. 但工程实践中增压器内部流场多表现出复杂的三维粘性流动特性， 导致定常分析方法的流场计算结果精度降低. 非定常流动计算方法克服了定常计算方法的缺陷， 并能得到相同周期内不同时刻各参数的变化情况， 使研究者能全面掌握增压器内部流动结构及损失机理. 因此， 近年来， 增压器内部流场分析中非定常流场分析技术得到了极大的关注. 祁明旭等[3]应用相延迟方法， 对高转速近失速点工况下压气机内部的三维非定常流动进行了数值模拟及频谱分析. 赵振国等[4]采用混合面方法、 转子冻结方法和非定常方法处理转/静交界面对车用涡轮增压器向心涡轮流场计算结果的影响. 但这些非定常计算的计算时间长， 对计算机的资源要求高， 且对能够用于计算网格的模型限制条件多. 非线性谐波法是在 Giles[5]研究基础上， 由He[6]提出的一种非定常分析方法， 其广泛应用于叶轮机械的非定常计算[7]. 王雷等[8]采用非线性谐波法对跨风速压气机进行计算， 并试验验证了计算精度. 赵军[9]分析了转/静交界面处理方法对非线性谐波法计算精度的影响. 药晓江等[10]采用非线性谐波法对双级跨风速风扇以及民用领域不可压缩流体条件下的液力涡轮进行非定常计算， 探讨非线性谐波法与传统双时间步法相比具有的优势， 以及谐波阶数对计算的影响.

本研究以轴向VNT为研究对象， 针对其涡轮内部非定常流动， 采用非线性谐波法进行非定常数值模拟研究. 分析不同谐波阶次下的结果， 通过考虑计算成本与计算精度， 以优选谐波阶次. 将优选的谐波阶次结果与实验结果进行对比， 探讨此方法应用于低速涡轮非定常流动模拟的可行性， 并细致分析此流动的非定常现象.

1 计算模型与方法

1.1 非线性谐波理论

非线性谐波法[11]是用于处理转静交界面的方法， 主要应用于轴流式旋转机械的研究中， 其主要思想是： 非定常流动由时均值和脉动值组成， 将N-S方程由时域转换成频域， 通过各个时间频率可得输运方程， 并通过傅里叶级数的阶数来控制非定常流动的求解精度， 在求解时均方程的同时， 分别求解每个频率下的两个守恒方程[12].

U(r，t)=U(r)+∑U′(r，t)

(1)

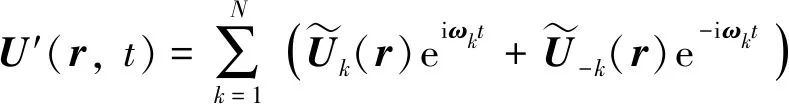
(2)

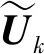
(3)

其中：Ωi为网格单元体积；Fc和Fv分别是离散的对流项和黏性项；S为面积；Q为源项. 相应时均方程为：

(4)

扰动方程对各扰动项为线性化方程， 分别求解两个扰动量f′和g′的傅立叶展开式， 形如：

(5)

由于傅立叶变换的正交性， 扰动f′和g′生成的可确定性应力项， 可以直接由傅立叶分解求得：

(6)

图1 低速工况计算模型局部图Fig.1 Local diagram of the model at low speed

其中：f、g为扰动的幅值;f′和g′之间的相角φfg可由叶片通过频率确定. 通过傅立叶分解， 将线性化方程投影到频域， 则谐波方程演变成为定常的形式， 于是可用时间推进法进行求解.

(7)

1.2 计算模型

研究主体为某型轴向可调喷嘴涡轮增压器， 该增压器可以通过调节涡轮端喷嘴环叶片的轴向位置， 以匹配发动机的运行工况. 其三维模型及几何原始数据是通过三坐标测量仪和二维投影仪精确测量所得， 借助逆向建模的方法完成模型的创建[13].

1.3 计算方法

通过该涡轮三维模型的几何特征在FINE/AutoGrid5建立计算网格模型， 其计算网格模型局部图如图1所示. 由于本研究的主要内容是涡轮内部流场分析， 而带蜗壳进行非定常计算的计算量大. 因此， 仅对涡轮级进行数值模拟， 单通道喷嘴环叶片网格数为250 629， 单通道涡轮叶片网格数为416 463， 综合计算速度和求解精度的考虑， 选择Spalart-Allmaras湍流模型. 定常流动计算中的转/静交界面采用混合平面法， 非定常流动计算中转/静交界面采用非线性谐波法. 通过增压器实验采集的进出口数据结果设定为计算模型的边界条件， 给定总温、 总压、 进气气流角. 其中， 进气气流角度通过蜗壳几何模型进行计算. 转/静交界面为一维无反射条件， 固体壁面设定无渗透、 无滑移物面边界条件.

2 结果分析

2.1 不同谐波阶次的分析

采用非线性谐波法对涡轮内部流场进行求解， 选取合适的谐波阶次大小对数值模拟的结果真实性至关重要. 谐波阶次越大， 非定常扰动逼近的结果精度越高， 流场捕捉的流动细节更加丰富， 数值模拟的结果更接近真实流场情况， 但是计算时间更长， 占用计算机的内存更大. 占用内存的定量值为定常求解内存、 谐波阶次、 扰动排数之间的乘积. 谐波阶次值小， 虽然计算速度快、 占用计算机内存小， 但是数值模拟的结果失真度更大， 非定常扰动逼近的精度更差. 因此， 一般选择谐波阶次小于5[14]. 其不同谐波阶次(H2、 H3、 H4、 H5)的涡轮特性相关计算结果如表1所示.

表1 低速工况涡轮特性计算相关参数

通过数值计算得到喷嘴环叶片及涡轮叶片叶中截面在不同谐波阶次下的非定常压力扰动情况， 如图2～5所示， 横坐标为相对弦长， 纵坐标为压力扰动与参考压力的比值， 参考压力设置为进口压力. 通过不同谐波阶次的求解结果， 分析其压力波动情况以表征计算精度， 并结合表1中数值计算的时间， 通过对计算时间与计算精度的综合衡量， 选择最佳的谐波阶次用于后续的流场内部的流动特性研究.

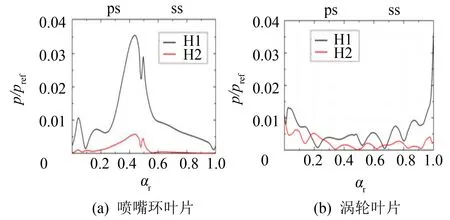
图2 前2阶谐波的压力扰动Fig.2 Pressure amplitude of H1 and H2

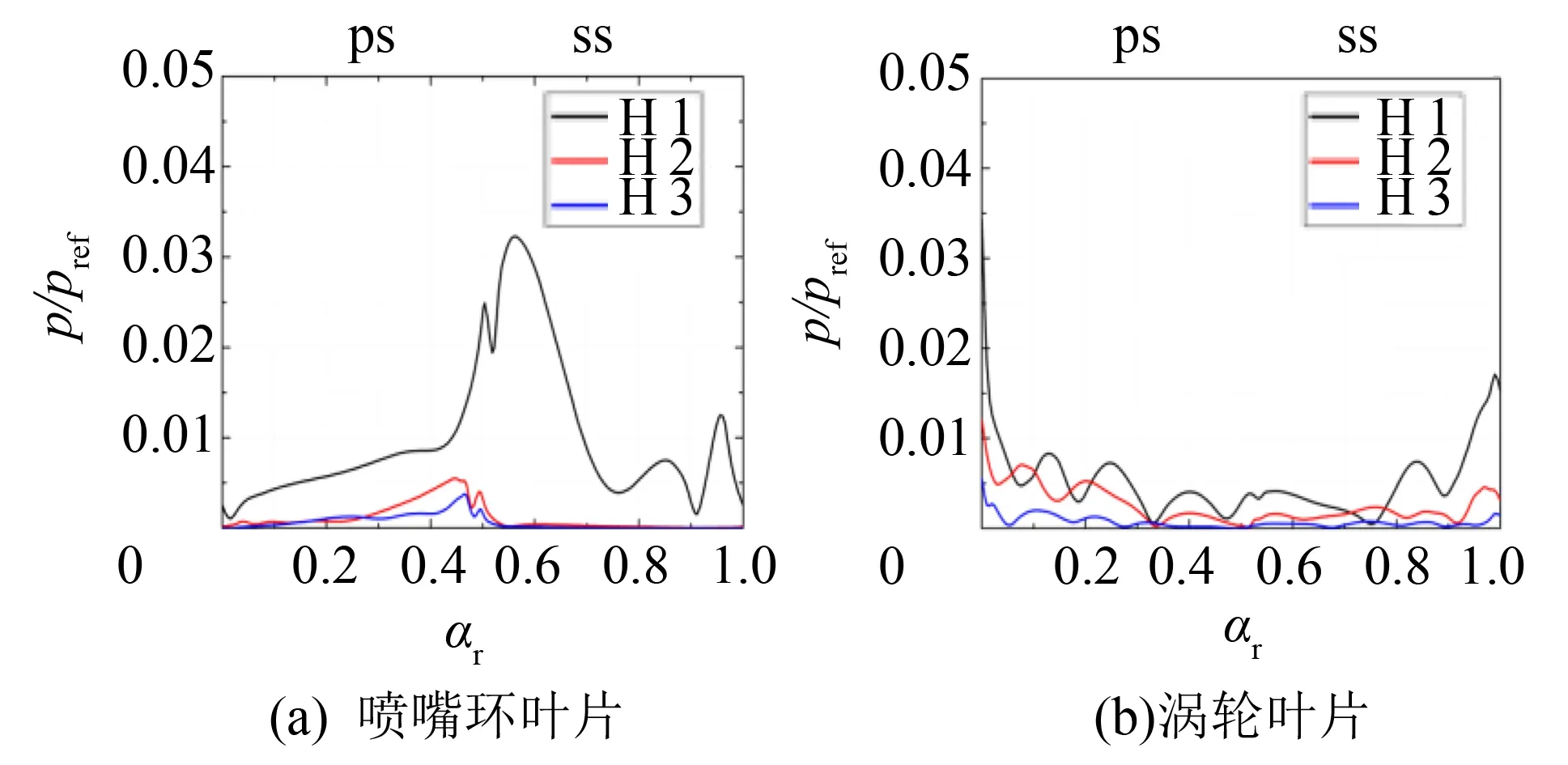
图3 前3阶谐波的压力扰动Fig.3 Pressure amplitude from H1 to H3

由图2可见， 一阶谐波的压力扰动在叶排间占主导地位， 涡轮叶片排对喷嘴环叶片排的势流干扰主要集中在一阶， 并且干扰区域主要在喷嘴环叶片的后半弦长. 从一阶谐波对涡轮叶片排尾缘(相对弦长为1.0)位置和喷嘴环叶片排前缘(相对弦长0.5)位置的影响可以看出： 涡轮叶片排对喷嘴环叶片尾迹的切割形成了涡轮叶片排之间的非定常流动特性. 二阶谐波对叶片排间的压力扰动幅度较小， 但在涡轮叶片排的前缘部分(相对弦长为0.0)位置处的影响依旧明显. 由图3可见， 一阶及二阶扰动量与前文所述无明显差别， 三阶扰动量对喷嘴环叶片排与涡轮叶片排之间的非定常压力扰动微弱， 几乎趋于0， 因此采用三阶谐波对计算径流式涡轮内流时具有较好的计算结果. 从图4和图5可见， 即分别采用四、 五阶谐波进行求解时， 其四、 五阶压力扰动量对喷嘴环叶片排及涡轮叶片排间的压力扰动非常微弱， 都可以得到精确的计算结果. 但是依据计算精度并综合计算时间因素发现， 采用四阶谐波进行计算时， 其计算时间约为三阶谐波计算时间的1.7倍， 而五阶谐波的计算时间约为三阶谐波计算时间的2.4倍.

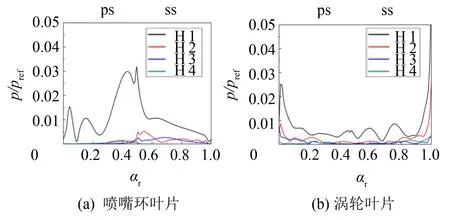
图4 前4阶谐波的压力扰动Fig.4 Pressure amplitude from H1 to H4

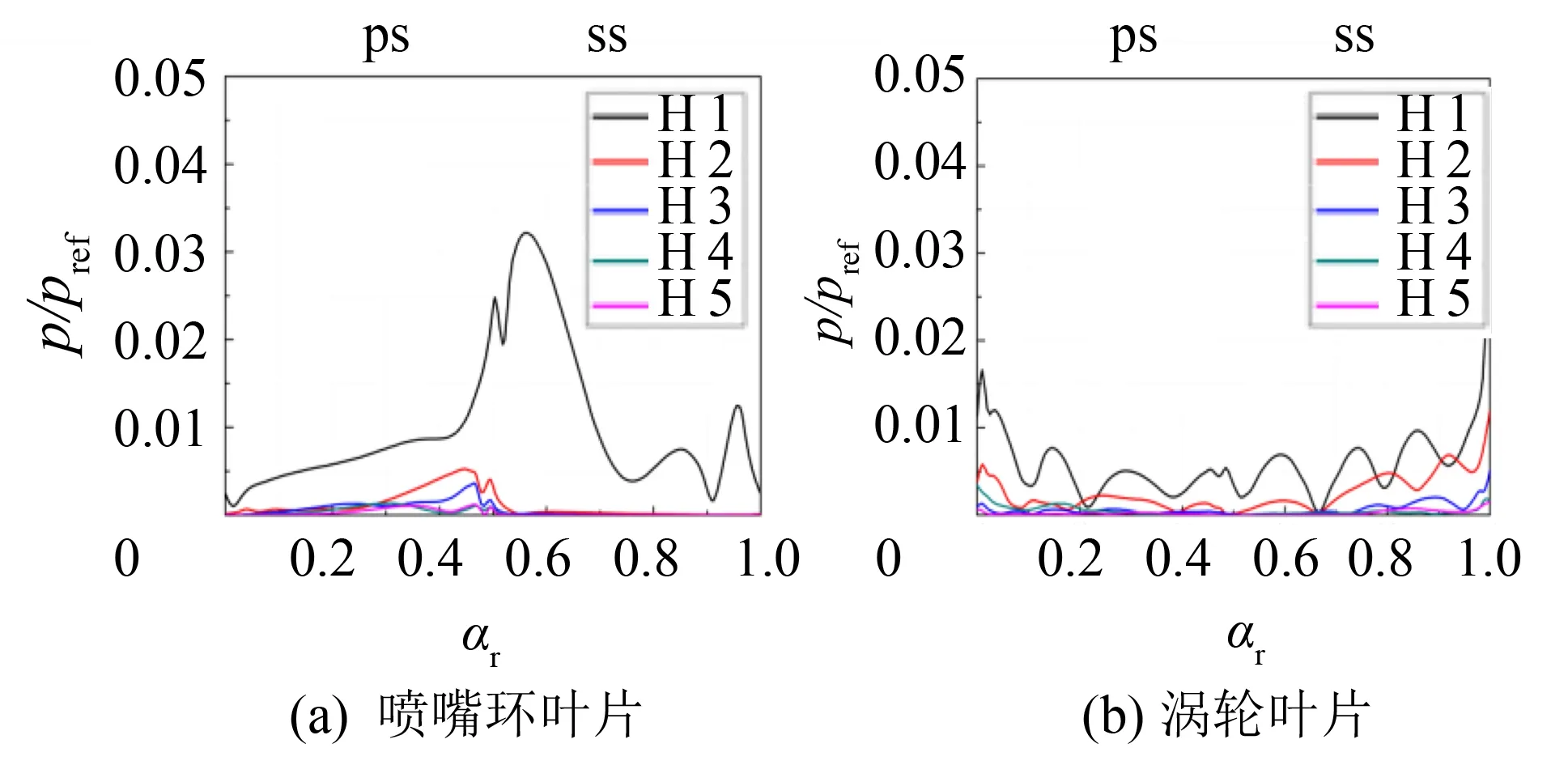
图5 前5阶谐波的压力扰动Fig.5 Pressure amplitude from H1 to H5

综上所述， 对轴向可调喷嘴的径流式涡轮增压器涡轮流动特性进行求解时， 选择三阶谐波阶次逼近的方案对计算时间和计算精度双重因素的考虑都有较好的结果.

2.2 方法验证

2.2.1增压器涡轮性能试验

涡轮性能试验平台由风源系统、 燃烧系统、 润滑系统、 管路系统、 测控系统、 测试用增压器及试验台附件系统组成. 进行增压器涡轮性能试验获取实验数据的目的主要有： 确定计算模型中边界条件的参数， 验证计算模型的真实度.

涡轮特性实验的操作规范及试验方法是依据国标GB/T 23341.1-2009[15]涡轮增压器技术条件及国标GB/T 23341.2-2009[16]涡轮增压器试验方法， 采用空气压缩机作为涡轮增压器的动力源， 以压气机为测功机， 获取涡轮效率. 选择增压器涡轮试验转速为60.5 kr·min-1， 保证涡轮进口气体参数稳定， 依据气源供气压力的实际条件， 测取涡轮进口压力、 涡轮出口压力、 涡轮流量及涡轮转速等数据[17-18]. 在试验条件允许的范围内选取5个工况点测量数据， 同时用国标中特定公式计算相关的试验数据, 制取涡轮效率特性趋势图.

2.2.2实验与计算数据对比分析

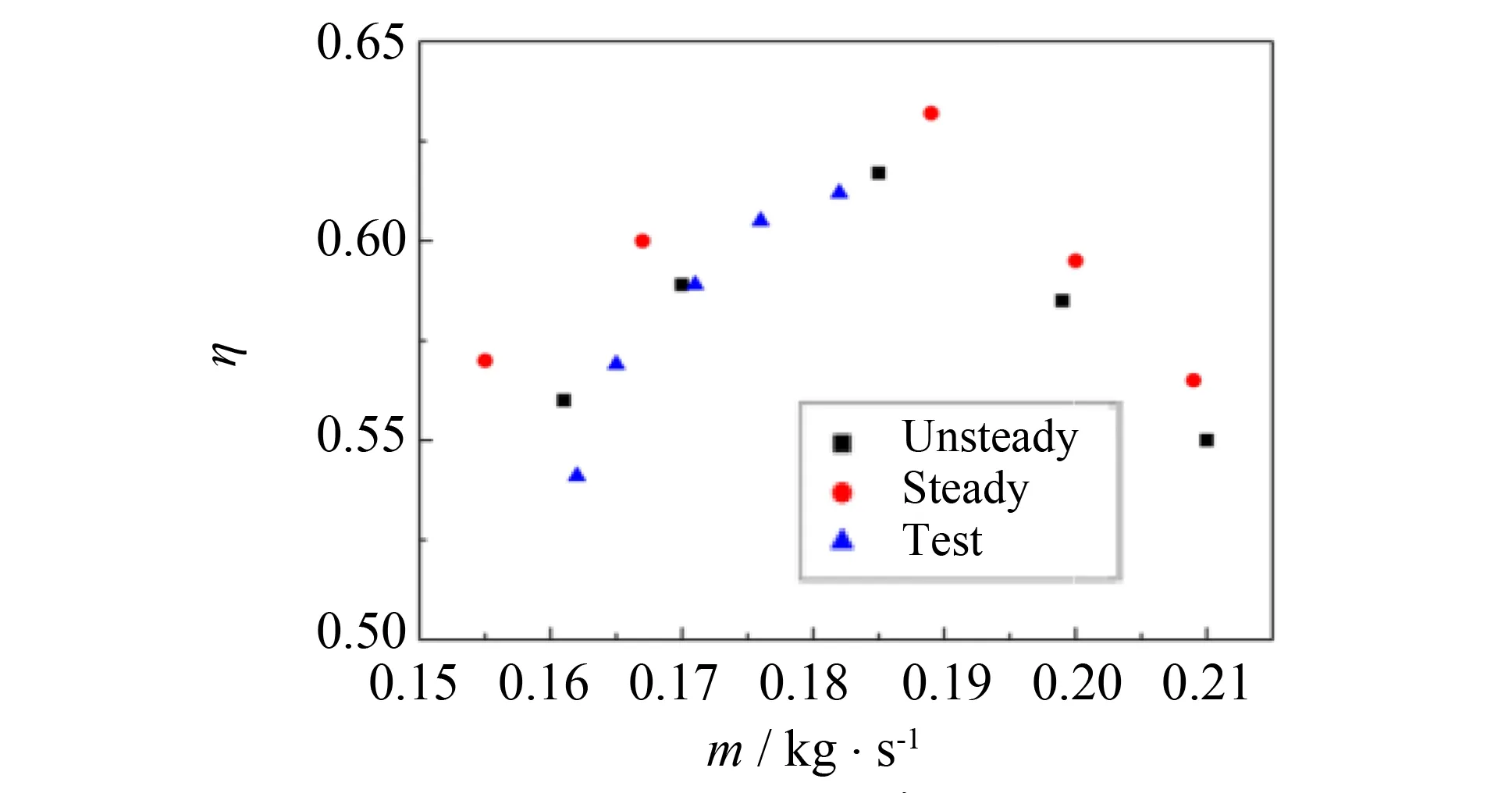
图6 涡轮效率特性(n=60.5 kr·min-1) Fig.6 Turbine efficiency characteristics (n=60.5 kr·min-1)

通过计算值与试验值对比验证模型有效性. 在保持计算网格模型及各参数设定相同的情况下， 采用定常流动、 非定常流动的计算方法对涡轮多工况点进行计算， 通过逐渐改变压气机出口背压的方式获取涡轮特性相关数据. 其中， 非定常数据的获取在确定谐波阶次之后计算所得， 将定常流动、 非定常流动的计算方法获取的涡轮特性数据， 与增压器性能试验台采集的涡轮特性数据进行对比， 如图6所示.

从图6可见， 通过对涡轮计算模型进行非定常计算、 定常计算得到的计算值， 以及采用增压器进行实验而采集、 处理得到的试验值， 数据点在图中呈现的走势相同. 涡轮试验的数据结果与采用非定常计算的结果吻合度较高， 最大误差为1.7%. 采用定常方法计算， 最大误差为2.8%， 虽然也处于允许的误差范围内， 但是计算精确度与非定常计算方法存在一定差距. 同时发现， 采用非定常计算方法计算的效率值比定常计算值小， 主要原因是非定常计算结果对流动损失细节的捕捉更细致， 流动损失更切合实际. 通过定常与非定常计算的结果与实验值进行对比， 可以确认该计算模型的有效性， 同时进一步说明非定常流的计算理论在径流式增压器的计算精确度上具有优越性， 非线性谐波法能够应用于径流式增压器涡轮的内流计算.

3 非定常方法分析涡轮内流场

增压器处于低速工况运转时， 此时发动机排气能量较低， 主要考虑喷嘴环叶片对气流的加速作用， 使高速流动的气流冲击涡轮， 以提高涡轮增压器转速， 从而提升增压器的涡轮效率. 而当增压器处于高速工况下， 发动机排气能量高， 损失的部分能量相对发动机排出的废气中的大量能量而言， 对增压器涡轮效率的影响较小. 因此， 主要针对涡轮增压器转数为60.5 kr·min-1的低速工况下涡轮内部流动特性进行求解. 依据所得出的结论， 采用三阶谐波对涡轮内部非定常流动特性结果进行分析. 增压器处于高速工况下的研究内容和研究方式与增压器处于低速工况下的研究为重复性研究， 受篇幅所限， 在此不再阐述.

3.1 S1流面熵等值线分布

熵分布图可直观看出涡轮内部的流动损失情况， 而对熵的非定常结果分析可看出一个周期内熵值随时间的变化情况. 通过S1流面的叶中截面熵分布的提取， 分析相同周期内不同时刻叶片通道内气流的流动损失情况. 一个周期T内不同时刻S1流面的熵等值线分布情况如图7所示.

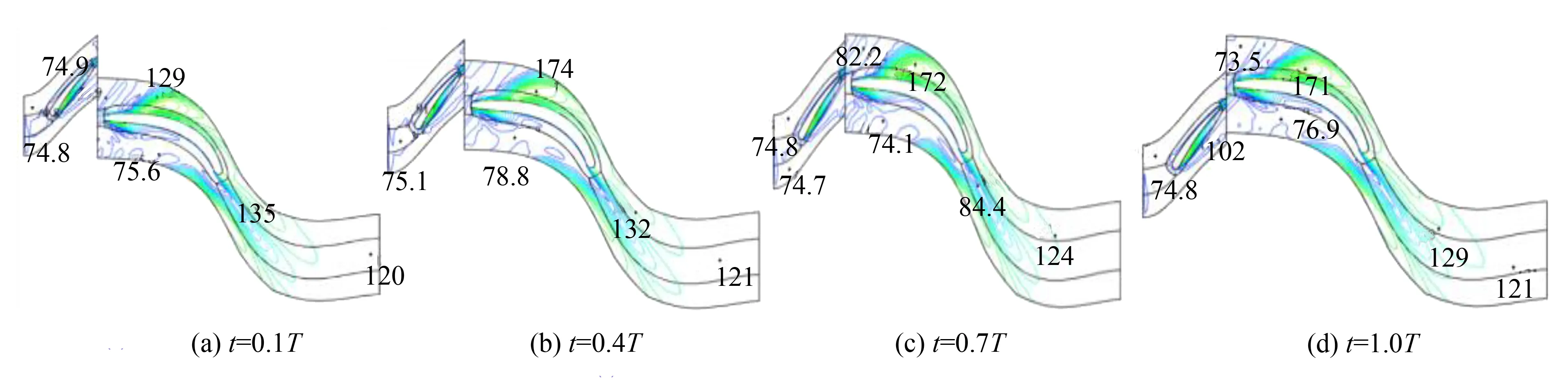
图7 S1流面熵等值线分布(单位： J·mol·K-1)Fig.7 Distribution of entropy isogram on S1 stream surface (Unit: J·mol·K-1)

由图7可见， 在喷嘴环叶片通道内流动较为顺畅， 无大面积高损失区域， 但在喷嘴环叶片的压力面形成了局部高熵区， 形成流动损失的原因是喷嘴叶片前缘存在攻角， 引起气流的流动分离现象， 形成局部低速区； 在尾部形成高熵区的原因是气流在喷嘴环叶片前缘分离的气流在尾缘处与主流区的高速流进行掺混. 喷嘴环叶片的尾迹周期性的冲击涡轮叶片前缘， 严重扰乱涡轮叶片通道内的流动， 主流区的高速流在涡轮叶片前缘形成流动分离， 分别沿着叶片的压力面和吸力面移动， 在气流向涡轮叶片尾缘迁移的过程中， 在吸力面形成的流动损失区域较压力面更大， 主要是流体在横向压力梯度的作用下被压至吸力面； 压力面的高熵区在周期内随时间的推移， 高熵区逐渐向涡轮叶片尾缘处移动， 而吸力面的高熵区几乎保持在同一区域内， 主要是由于吸力面的流体速度快， 能量迁移的速度快. 而在尾部形成高熵区的原因是气流分别沿着叶片的压力面和吸力面移动至尾缘处与主流区的高速流进行掺混. 综上所述， 喷嘴环叶片通道内主要是受到动叶前缘微弱的势流干扰， 而涡轮叶片通道受到喷嘴环叶片尾迹的强烈的干扰. 喷嘴环叶片通道内的流动特性较涡轮叶片通道更稳定， 主要是在设定边界条件时， 给定的入口来流是稳定且均匀的.

3.2 涡轮通道各截面流动图谱

涡轮气动性能和效率的决定因素是能量的利用率. 涡轮内部流动具有复杂的三维粘性流动特征. 因此， 控制和降低涡轮内部流动的损失， 需要详细地分析涡轮内部的流动特性， 而二次流在通道截面的投影能够捕捉到涡轮内部流场的涡系形成和发展， 表征出流动损失的区域， 所以针对同周期不同时刻的涡轮通道不同截面流动图谱进行分析. 涡轮通道内流道截面不同截面处同一周期内不同时刻的流动图谱如图8～11所示. 其CUT1、 CUT2、 CUT3截面为截取涡轮通道的位置， 如图8所示.

图8 涡轮通道的截面位置Fig.8 Position of the interception in the turbine channel

图9为涡轮叶片通道内CUT1截面同周期不同时刻的二次流及其涡系分布， 气流在离心力作用下从轮毂向轮缘处迁移， 涡轮叶顶间隙流从吸力面在横向压力梯度的作用下穿过叶片间隙被压至压力面， 并与从轮毂向轮缘流动的气流进行掺杂， 在靠近压力面形成泄漏涡， 形成原因主要是负攻角太大. 图10为涡轮叶片通道内CUT2截面同周期不同时刻的二次流及其涡系分布. 随着涡轮通道区域的逐渐扩大， 在气流的推动下使角涡不断向上迁移. 受到涡轮弯曲叶型的影响， 涡轮叶顶间隙流在离心力及横向压力梯度的作用下向吸力面移动， 并在涡轮通道内靠近压力面形成通道涡， 主要是由于涡轮叶轮通道边界层内的低能流体所产生的惯性力不足以克服压力面与吸力面之间的横向静压梯度， 造成低能流体向低压区流动， 而外部间隙泄漏流所提供的高能流体会向高压区进行补偿， 相互作用形成的. 在同一周期不同时刻二次流及涡系的形成和发展可以看出， 通道涡不断发展， 影响范围不断增大. 图11为涡轮叶片通道内CUT3截面同周期不同时刻的二次流及其涡系分布， 涡轮通道内的通道涡在压力面向吸力面横向移动， 叶根处低能流体由于横向压力梯度的作用， 此时， 气流所承受的离心力不足以提供气流迁移至叶顶的能量， 并且在通道涡的影响下， 在轮毂与吸力面之间形成角涡. 在同周期不同时刻二次流及涡系的形成和发展可以看出， 角涡和通道涡影响范围不断增大.

图9 CUT1截面处不同时刻流动图谱 Fig.9 Flow atlas at different time in CUT1 section

图10 CUT2截面处不同时刻流动图谱Fig.10 Flow atlas at different time in CUT2 section

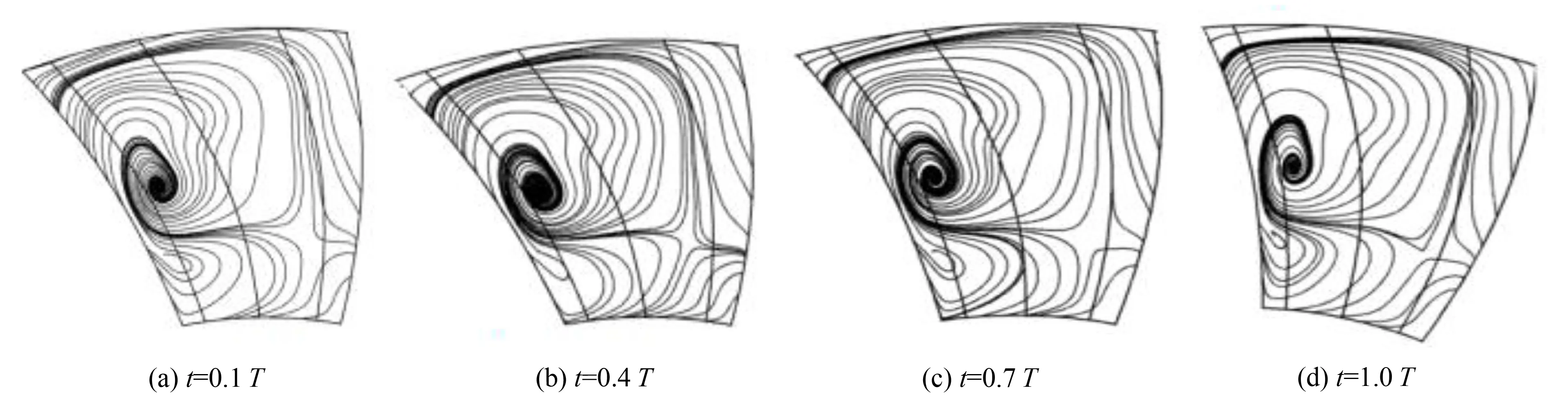
图11 CUT3截面处不同时刻流动图谱 Fig.11 Flow atlas at different time in CUT3 section

4 结语

1) 在计算径流式涡轮内部流动特性时， 运用三阶谐波逼近的方案对计算精度和计算时间双重因素的考虑都有较好的结果.

2) 通过非定常计算方法获取的涡轮特性数据与试验数据吻合度更高， 较定常计算方法准确性更好， 也进一步说明非线性谐波法能够用于径流式涡轮增压器涡轮的内流计算.

3) 通过细致地剖析增压器涡轮内部流动情况， 结果表明： 喷嘴环叶排与涡轮叶排间形成的非定常流动特性明显； 涡轮内部涡系结构在同周期内随时间发生变化， 并捕捉到造成涡轮内部流动损失的通道涡、 角涡、 泄漏涡的形成与发展.