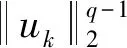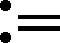带有组合非线性项的一类基尔霍夫方程径向解的存在性

2019-05-23 11:36刘紫玉

重庆理工大学学报(自然科学) 2019年4期

关键词：有界客户经理径向

刘紫玉，韩伟

(中北大学理学院，太原 030051)

在本文中，研究了如下基尔霍夫方程：

(1)

其中b>0, 1

①V(x)∈C(RN,R)，并且对于∀x∈RN有V(x)=V(|x|)>0；

⑤Γ定义如下：

则存在l∈(Γ,V∞)，使得

⑥f(x,u)=f(-x,u)。

1883年基尔霍夫在文献[14]提出了如下数学模型：

(2)

Li等[4]利用A.Azzollini’s想法研究了如下非线性基尔霍夫方程径向解的存在性：

(3)

其主要是利用了一个截断函数获得有界的(PS)C序列。

文献[3]研究了非线性项f(u)满足Berestycki-Lions条件的基尔霍夫方程，得到了至少一个解的存在性：

(4)

为了便于理解，首先介绍如下基本定义：

(5)

(6)

本文的主要结论如下：

定理1假设①～⑥条件都成立，则存在m>0和b*>0使得对∀K(x)当|K|2/(2-q)

1 预备知识

引理1(Sobolev嵌入定理)有如下连续嵌入:

(7)

(8)

引理3(Fatou引理)设{fn}是一个非负可测函数序列，则

(9)

定义1((PS)C条件) 设E是Banach空间，E-1是其对偶空间。I∈C1(E,R)以及c∈R，如果{uk}⊂E满足

I(uk)→c和I′(uk)→0 (inE-1, ask→∞)

称序列{uk}是泛函I的(PS)C序列；如果泛函I的任意(PS)C序列在E中有收敛的子列，称泛函I满足(PS)C条件。

引理4设E是Banach空间，E-1是其对偶空间。假设I∈C1(E,R)，并且存在α<β，e∈E以及ρ>0，||e||>ρ使得

设Λ={γ∈C([0,1],E)∶γ(0)=0,γ(1)=e}，表示连接0到e的连续路径的集合，并且令c≥β，c作如下定义：

则存在一个序列uk∈E使得

I(uk)→c和I′(uk)→0 (inE-1, ask→∞)

引理5(嵌入不等式) 设H1连续的Sobolev嵌入Ls(RN)(2≤s≤2N/(N-2))空间中，则存在一个常数cs使得

||u||s≤cs||u|| ∀u∈H1

其中

2 定理的证明

在这部分，将给出定理1的证明过程。为此，先给出如下：

因此

(10)

根据Hölder不等式和Sobolev不等式有

(11)

(12)

其中1

引理7泛函I的有界(PS)序列有收敛的子列。

又因为〈I′(uk),uk〉=o(1)和〈I′(uk),u〉=o(1)，有

(13)

(14)

令

▽uk·▽(uk-u)+V(x)uk(uk-u))dx=o(1)

(15)

(16)

(17)

(18)

事实上，根据Hölder不等式有

此外，丽江供电局注重提升优质服务，严格落实客户经理制，通过微信客户服务群、客户经理名片、公示牌等多种方式开展客户分群管理，第一时间响应客户诉求，让客户用上“放心电，满意电”。自2017年以来丽江市场营销部共建立微信群23个，参与人数5231人，发放客户经理名片15200张，粘贴客户经理公告136份，组织安全用电宣传活动50余次，发放安全用电宣传单25000余份。