基于智能体理论的空气悬架车身高度智能控制系统研究
江 洪,王鹏程,李仲兴
(江苏大学 a.机械工程学院; b.汽车与交通工程学院, 江苏 镇江 202013)
悬架作为底盘系统的主要部件之一,对行车过程中行驶平顺性与操纵稳定性有着重要影响。空气悬架由于其固有频率低,变刚度等优良特性,已经普遍使用在大型客车、高档轿车上[1]。高度调节功能作为空气悬架的特色功能之一,对车辆行驶过程中的平顺性、操稳性以及通过性具有重要的意义,这使得车身高度调节成为研究热点。国内外学者在车身高度调节系统非线性建模,系统的设计与完善等方面做了大量的工作,取得了丰富的研究成果。2008年,汉江大学的鲍卫宁等[2]以机械式高度阀控制的空气悬架系统为研究对象,建立了模块化耦合空气悬架模型。2010年江苏大学徐兴[3]基于微分几何理论以及变结构控制理论,提出了三点测量的ECAS车身高度独立变结构控制以及耦合变结构控制策略,同时以该控制策略为核心设计了ECAS客车车身高度控制系统,取得了良好的控制效果。2011年,韩国汉阳大学Kim等[4]以小型轿车车身高度控制系统为研究对象,提出了一种容错控制算法,进一步提升车身高度控制系统的安全性和可靠性。2017年,江苏大学的孙晓强等[5]将模糊理论以及变结构控制理论相结合,提出模糊滑模变结构控制算法,该算法可以有效地抑制滑模控制器抖振的影响,提高车身高度控制器的适应性。
目前,国内外学者已经提出了诸多提升车身高度调节系统的调节品质与系统稳定性的方法。但是从提高车身高度调节系统适应性这一角度出发的研究却很少。在传统的悬架设计中,为了满足行驶要求,常常需要保证足够大的限位行程。利用空气悬架高度可调的特性,辅以合适的方法,可以实现车身高度随工况变化,并能自适应调节。这样可以充分利用悬架行程,不仅能获得良好的乘坐舒适性,而且能得到更好的空气动力学特性以及更低的重心[6]。智能体理论与技术的发展为此项研究提供了新的研究途径与方法。智能体理论作为人工智能和计算机科学的前沿领域,一直是国内外学者研究的热点[7]。智能体相关理论的研究一般涉及领域广泛,重视多学科、多领域间的横向联系与合作运用。针对智能体系统的开发通常会涉及智能体的体系结构、学习机制等问题。BDI模型[8]是由Bratman在1987年提出的,是一种被广泛使用的慎思型智能体模型。该模型将理性主体分为信念(belief)、愿望(desire)以及意图(intention)3个部分,能够较为清晰地描述理性主体的逻辑思维过程。基于BDI模型的研究一般分为理论与应用两个层面,理论层面主要研究如何使用逻辑方法对BDI模型进行形式化的描述。应用层面主要涉及智能体系统结构设计以及编程实现方法。强化学习是一种在不知道正确方案的外部指导存在的情况下基于“尝试—评价”循环的学习行为[9]。强化学习已经广泛使用在交通规划、智能机器人、无人驾驶等领域。
本文首先建立了空气悬架7自由度模型以及空气悬架高度调节模型,并通过试验验证了空气悬架7自由度模型的准确性。在此基础上基于BDI模型以及强化学习算法设计了目标车身高度控制智能体,并构建空气悬架车身高度智能控制系统。其中,目标车身高度控制智能体通过评价指标来更新自身信念,产生相应的愿望,并通过学习行为来完善知识库,最终依靠自身信念、愿望、知识做出决策确定智能体意图,获得目标车身高度,从而可以自适应地调节车身高度,获得良好的综合性能。
1 空气悬架车身高度调节系统
1.1 整车7自由度模型
根据研究的需求建立了包含车身侧倾、俯仰、质心位置处的垂向运动以及4个车轮垂向运动的7自由度整车模型,由式(1) (2)来描述。
(1)
(2)
式中:Mb为簧上质量;Zs为簧上质量质心的垂向位移;θ、φ分别为车身的侧倾角和俯仰角;d为车轮1/2轮距;a、b分别为簧上质量质心到前后轴水平方向的距离;Ix、Iy分别为侧倾转动惯量与俯仰转动惯量;F1、F2、F3、F4分别对应4个悬架作用于车身的悬架力;P1、P2、P3、P4、Pa分别为4个空气弹簧实际气压与初始气压;A1、A2、A3、A4分别为4个空气弹簧的有效面积;c1、c2、c3、c4为4个减振器的阻尼系数;fd1、fd2、fd3、fd4为4个悬架动行程;Kθgf、Kθgr分别为前后横向稳定杆的侧倾角刚度;Mt为车轮质量;Kt为车轮等效垂向刚度;Zt1、Zt2、Zt3、Zt4为4个车轮垂向位移;q1、q2、q3、q4为4个车轮受到的路面垂向激励。
1.2 空气悬架高度调节的数学模型
空气悬架高度调节系统是一个高度复杂的非线性时滞系统。该系统主要由电磁阀、管路、储气罐以及空气弹簧组成。忽略电磁阀的动态特性,电磁阀模型可以抽象地等效为一个节流小孔,通过电磁阀的质量流量与电磁阀上下游的气压有关。通过电磁阀的质量流量可用式(3)来描述。
(3)
式中:Ae为电磁阀的有效流通面积;pu为电磁阀上游绝对气压;pd为电磁阀下游绝对气压;Tu为电磁阀上游的气体温度;R为理想气体常数;k为多变指数。
空气弹簧作为一个可变气体质量系统,其体积、高度会随着车身高度调节过程实时变化。空气弹簧的动态特性可以通过式(4)来描述。
(4)
式中:TSP为空气弹簧内的温度;qm为流入或者流出空气弹簧的质量流量;PSP为空气弹簧内的气压;VSP为空气弹簧的体积。
空气弹簧体积变化近似看成容积变化率和垂直位移变化率的乘积,空气弹簧的体积变化可以用式(5)来描述。
(5)
储气罐为容积不变的气罐,由于气体交换速度很快,可以忽略储气罐放气过程中的热交换。根据热力学第一定律可得储气罐模型,由式(6)来描述。
(6)
式中:Ttk为储气罐内气体温度;Vtk为储气罐的容积;Ptk储气罐内的绝对气压。
车身高度调节系统内各部件由管路进行连接,连接管路不同位置处气体质量流量随时间变化的函数[10]由式(7)来描述。
(7)
式中:L为管路长度;Pdn为管路末端气压;Tdn为管路末端温度;c为声速;Rt为连接管路内壁阻力系数。
1.3 整车7自由度模型的试验验证
为了验证所建立的仿真模型的准确性,搭建了如图1所示的空气悬架整车试验平台。通过MTS320四通道道路模拟机向四轮施加激励。图2表示通过不平衡载荷模拟汽车转弯工况得到的车身侧倾角随侧向加速度的变化规律。表1表示模拟车辆以70 km/h的车速行驶在路面不平度系数为256×10-6m3的道路上时,簧上质量各位置处的振动情况。

图1 空气悬架车身高度调节系统试验台架
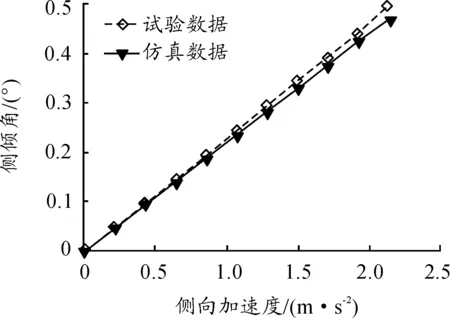
图2 空气悬架侧倾特性仿真与试验结果对比
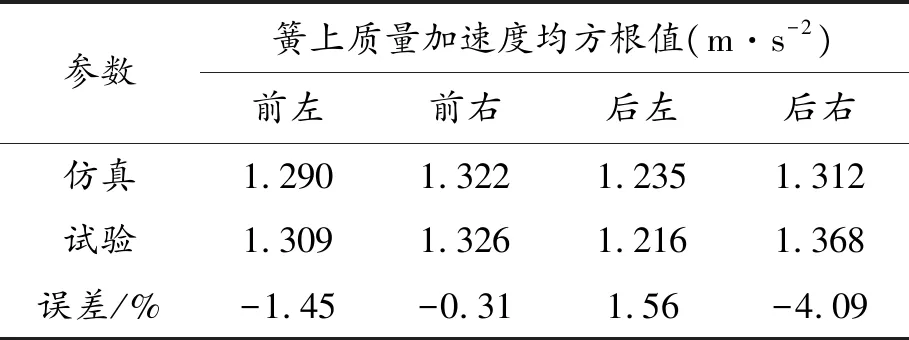
参数簧上质量加速度均方根值(m·s-2)前左前右后左后右仿真1.2901.3221.2351.312试验1.3091.3261.2161.368误差/%-1.45-0.311.56-4.09
由图2和表1可以看出:试验结果和仿真结果吻合度较高,仿真结果准确可靠,可以以此模型为基础展开后续研究工作。
2 基于智能体理论的车身高度智能控制系统设计
2.1 车身高度智能控制系统结构
车身高度智能控制系统主要由目标车身高度控制智能体以及车身高度调节系统组成。智能体一般被认为是具有一定计算能力的软硬件实体,能够感知周围的环境,可自治地运行,并通过自身动作来适应环境变化[11-12]。目标车身高度控制智能体通过传感器感知行车环境,产生适应相应环境的目标车身高度,再通过车身高度调节系统的调节,达到目标车身高度,从而提升车辆行驶过程中的综合性能。在BDI框架下构建如图3所示的空气悬架车身高度智能控制系统。
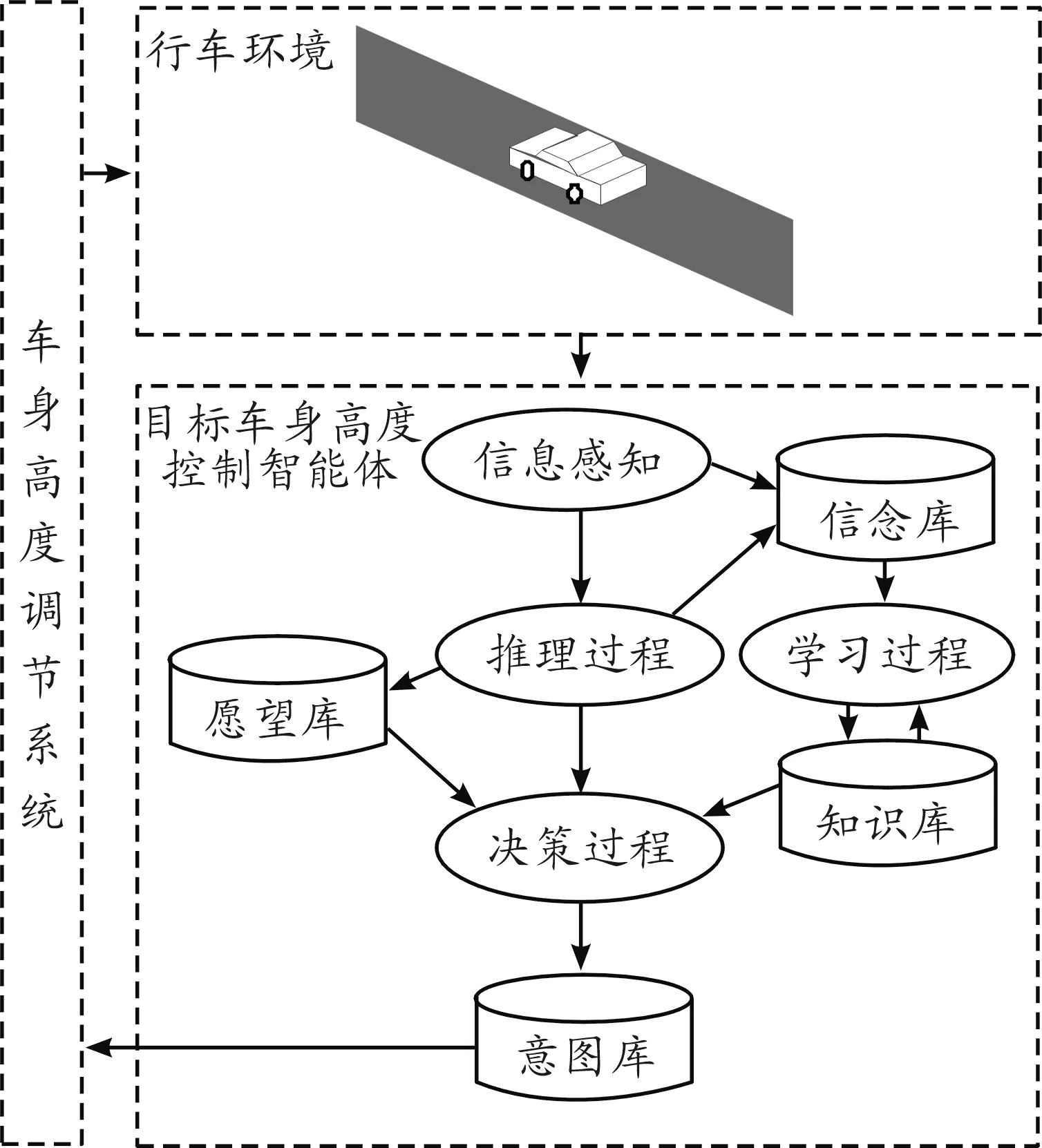
图3 空气悬架车身高度智能控制系统
从图3可以看出:目标车身高度控制智能体包含感知、推理、决策、学习4个智能体行为以及信念、愿望、意图、知识4个内部状态。目标车身高度控制智能体在行车过程中不断通过自身行为来完善自身状态。
信念:包含智能体获取的环境信息与自身信息的集合。目标车身高度智能体将通过信息感知获得的环境信息与自身信息存储到智能体的信念库中。知识作为经过处理的信念,通过智能体的学习行为,将信念库中存储的信息转化为智能体知识,并存储到知识库中。
愿望:代表智能体希望达到的状态。目标车身高度智能体将整车状态评价存入愿望库中,并根据评价来确定自身愿望。
意图:代表承诺的愿望,实现自身愿望的动作、方法。目标车身高度智能体以自身愿望与知识为依据,通过决策行为确定目标车身高度。
2.2 目标车身高度智能体行为建模
信息感知:目标车身高度控制智能体通过传感器获取车速信息v、簧下质量加速度信息ati(i=1,2,3,4)、车身侧倾角θ、簧上质量加速度信息ax、ay、az以及车身高度信息H。通过簧下质量加速度以及车速可以精确快速地辨识路面不平度[13]。车速、路面不平度与车身侧向加速度作为行驶工况信息,代表车辆可以获取的环境信息。车身侧倾角、簧上质量加速度以及车身高度作为可以获取的自身状态信息,确定目标车身高度作为智能体可以采取的动作。考虑到行车过程中行驶工况信息难以时刻保持恒定以及学习行为建模的需要,因此要将行驶工况信息以及智能体动作进行离散化。由于遍历一个N维空间的复杂程度将随着N呈指数增长[14],考虑计算量以及车辆实际行驶状况,将车速分为(0,30]、(30,60]、(60,90]、(90,120]、(120,+∞)5个等级区间。参考国标GB7031—2005《机械振动 道路路面谱测量数据报告》,将路面分为A、B、C、D以及其他路面共5个等级;将侧向加速度分为(0,0.1g]、(0.1g,0.2g]、(0.2g,0.3g]、(0.3g,+∞)共4个等级区间。将智能体的动作分为15个等级:从初始平衡位置开始,每隔5 mm,向上或者向下可以调节7个车身高度等级。
推理过程:行车过程中,智能体通过指标来评价车辆目前的行驶状态。参考国标GB/T4971—2009《汽车平顺性试验方法》,通过车身质心处簧上质量x、y、z三个方向的加权加速度均方根值来评价行驶平顺性,计算公式见式(8)。
(8)
式中axw、ayw、azw表示通过频谱分析获得的单轴加权加速度均方根值。
采用侧倾因子[15]来衡量车辆的侧倾运动,计算公式为
(9)
式中:hR为车身侧倾中心到地面的距离;hs车身质心到侧倾中心的距离;ays车身y方向的加速度。
目标车身高度控制智能体根据综合评价指标来判断当前车身高度是否满足自身愿望。综合评价指标采用加权的方式:
J=α·aw_nor+(1-α)·Rnor
(10)
式中:aw_nor、Rnor分别为归一化处理后的加权加速度均方根值以及侧倾因子;α为加权系数,α∈[0,1]。
学习过程:目标车身高度控制智能体根据信念库中的信息,通过“尝试—评价—再尝试”这一循环往复的动作来进行动态学习,完善自身知识库。由于路面激励的存在,即使车辆行驶工况以及车身高度没有发生变化,车辆综合评价指标的数值也在不断变化,因此一个工况下的最优车身高度必须从长期意义来考虑。汽车的振动过程无法用确定函数来描述,但是具有一定的统计规律,可以通过统计概率的方法来研究。汤普森抽样算法是一种基于贝叶斯理论的强化学习算法[16-17],在有限次尝试的过程中不仅可以减少智能体选择较差动作的次数,而且可以高效快速地找到该工况下的最优选择,最重要的是该方法能实现智能体在线学习行为,可以克服由于建模不准确而造成学习结果不准确的问题。基于汤普森抽样的目标车身高度控制智能体强化学习过程主要可以用图4来描述。
如图4所示,目标车身高度控制智能体按行驶工况,通过抽样、筛选、执行、更新的步骤进行学习,根据抽样结果来预测可以获得最大回报的动作,并通过执行动作的实际回报来更新知识库。在智能体学习之前,需要根据车辆行驶的实际情况来确定先验分布。
1) 确定初始先验分布
先验分布影响着智能体学习速度与最终的学习结果。大量的文献和试验结果表明路面不平度激励是一个各态历经的平稳随机过程[18],同时近似服从正态分布。利用仿真模型,分别在“16×10-6/m3路面不平度系数、30 km/h车速”,“16×10-6/m3路面不平度系数、70 km/h车速”,“16×10-6/m3路面不平度系数、70 km/h车速、0.2g侧向加速度”和“256×10-6/m3路面不平度系数、70 km/h车速”4种工况下,计算了加权加速度均方根值和侧倾因子的数值,并进行统计分析。统计分布如图5、图6所示,其中工况1~4与上文表述顺序一致。

图4 目标车身高度控制智能体强化学习过程
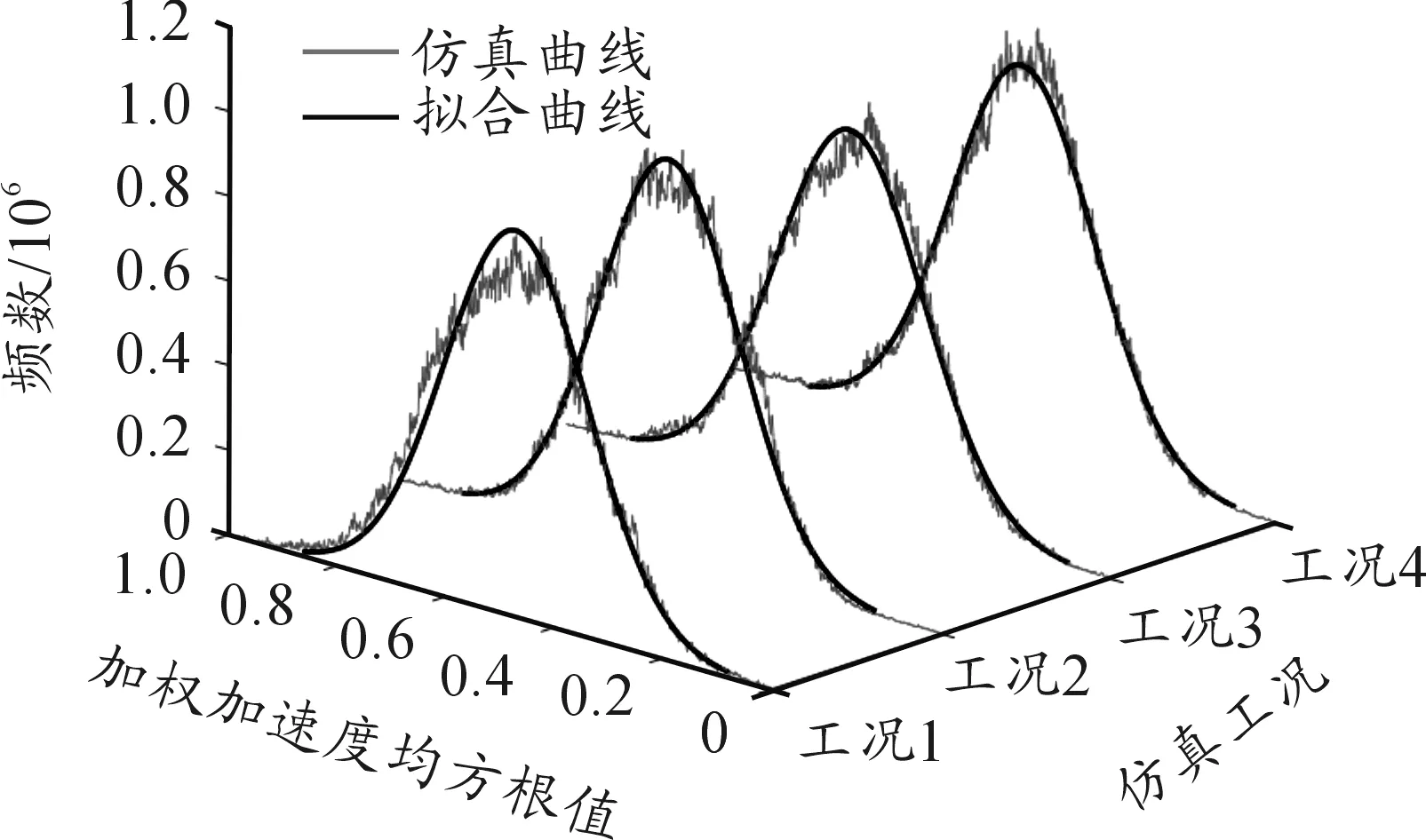
图5 不同工况下加权加速度均方根值的统计分布
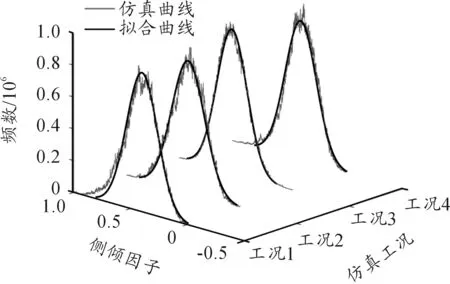
图6 不同工况下侧倾因子的统计分布
由图5、6可以看出,在不同车速、路面以及侧向加速度下,加权加速度均方根值和侧倾因子均近似服从正态分布,因此学习算法的初始先验分布选择均值为0、方差为1的正态分布。
2) 目标高度控制智能体的学习模型
定义:N(μi,1/(ki+1))为每个离散动作i的先验分布;xi(n)为第n次学习从第i个先验分布N(μi,1/(ki+1))中获取的随机样本;J(n)表示第n次学习所获得的综合评价;r(n)为第n次学习获得的实际回报。动作选择如式(11)所示。
i(n)=argmax(xi(n))
(11)
目标车身高度控制智能体执行完动作后,通过综合评价指标来表示动作回报,如式(12)所示。
(12)
通过实际回报来更新相应动作的先验分布,如式(13)(14)所示。
(13)
ki(n+1)=ki(n)+1
(14)
决策过程:表示目标车身高度控制智能体根据知识库以及愿望库中信息确定目标车身高度的过程。采用后验分布均值μ最大的动作作为智能体的输出。
3 仿真结果与分析
3.1 学习行为验证与效果分析
为了验证目标车身高度控制智能体学习行为的有效性,利用车身高度智能控制系统仿真模型,在“256×10-6/m3路面不平度系数、60 km/h车速”的工况下进行仿真。考虑实际条件与计算精度,设置仿真步长为1 ms,进行50 000次学习。图7是对整个学习过程中每个动作的执行次数的统计。图9 表示在不同算法构成智能体学习行为下,积累遗憾[19]随着学习次数增长的变化情况,其中“Rt值”由式(15)计算。
(15)
式中:Rt代表累计的遗憾值;wopt代表学习过程中获得的最大回报;wB(i)每次动作执行所获得的真实回报。
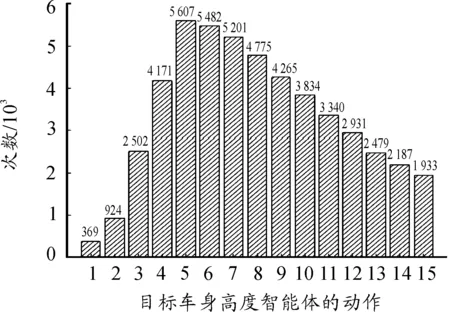
图7 智能体动作选择统计
从图7中可以看出:在整个学习过程中,动作5被智能体执行的次数最多,即动作5为该工况下的最优动作。从图8中可以看出:通过汤普森抽样算法构建的智能体学习行为,在相同学习次数下,积累遗憾值更低,在提高学习效率、节省学习时间的同时可以避免车辆在学习过程中过多选择较差动作,从而减少了车辆损伤。
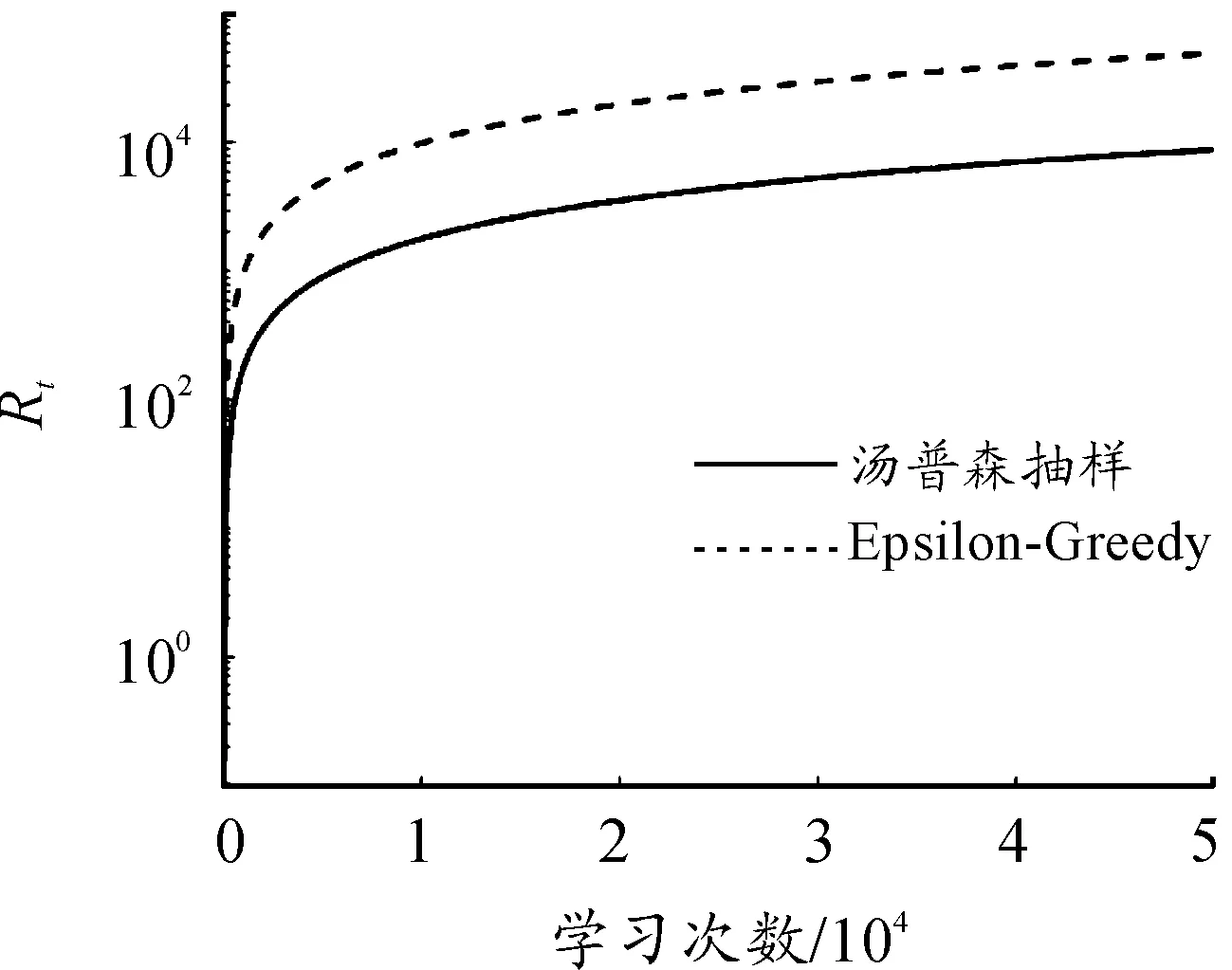
图8 目标车身高度智能体学习曲线
为了进一步确定智能体的学习结果的适用性,在同样工况以及智能体选择的最优动作下进行仿真,设置仿真步长为1 ms,仿真时间3 000 s。仿真结果如图9、10所示。
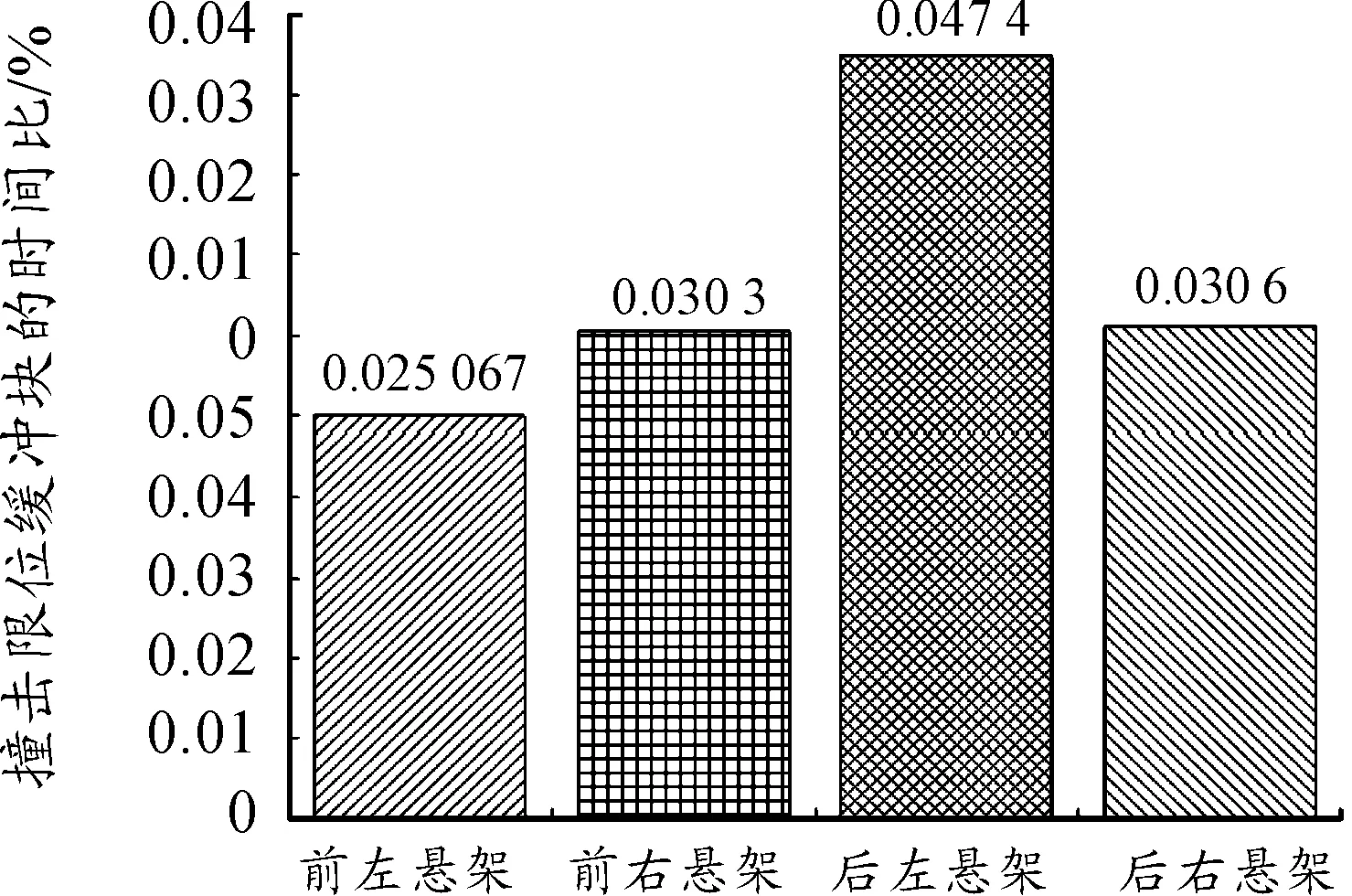
图9 撞击限位缓冲块频率图
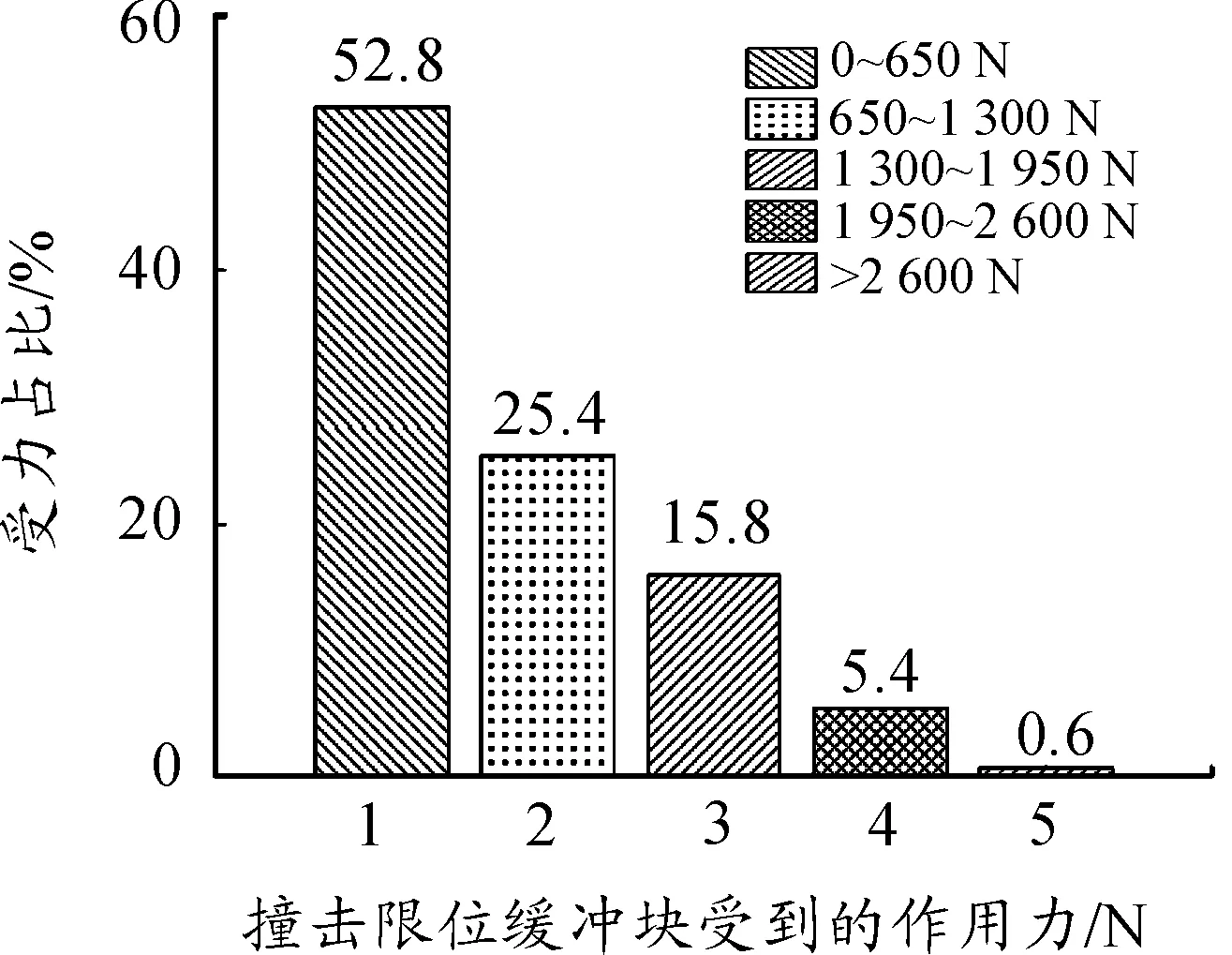
图10 限位缓冲块作用力分布图
从图9和图10中可以看出:在智能体选择的动作下,前左、前右、后左、后右悬架撞击悬架限位缓冲块的概率均小于0.1%,簧上质量受到的限位缓冲块的作用力主要集中在0~650 N的范围。在该工况下,目标车身高度控制智能体通过学习行为所确定的最优动作满足悬架动行程需求,具有一定适用性。
3.2 混合工况下智能控制系统的控制效果
为了验证车身高度智能控制系统的控制效果,在混合工况下进行仿真,比较传统空气悬架车辆以及装有车身高度智能控制系统车辆的性能指标。图11为所采用的混合工况下路面激励、车速以及侧向加速度随时间的变化情况。图12表示在图11所示工况中,在智能系统控制下车身高度变化情况。图13、14为仿真后20 s两种车辆性能指标对比。图15、16分别表示在混合工况内的不同工况下各性能指标的平均改善率。表2、3为整个仿真过程中,两种车辆性能指标对比。
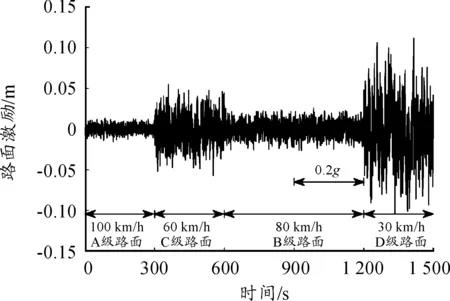
图11 混合工况
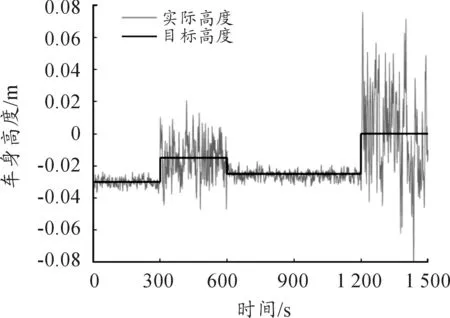
图12 混合工况下车身高度变化
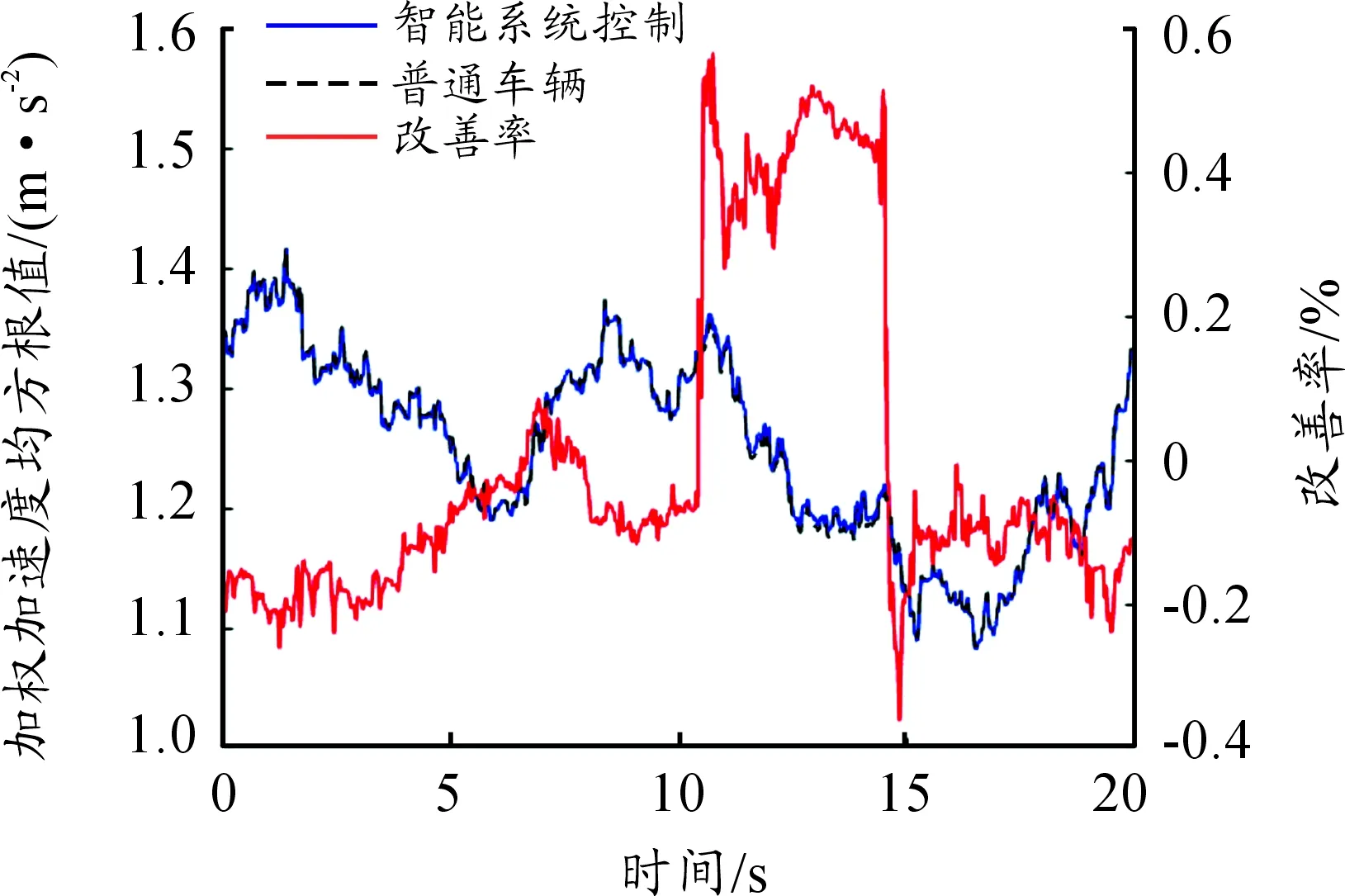
图13 加权加速度均方根值对比
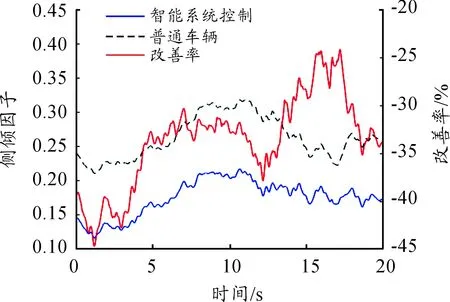
图14 侧倾因子对比
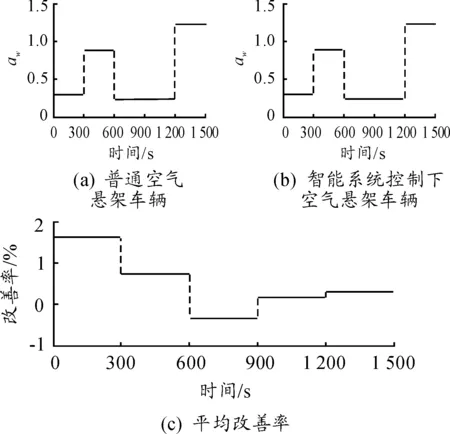
图15 不同工况下aw的平均改善率
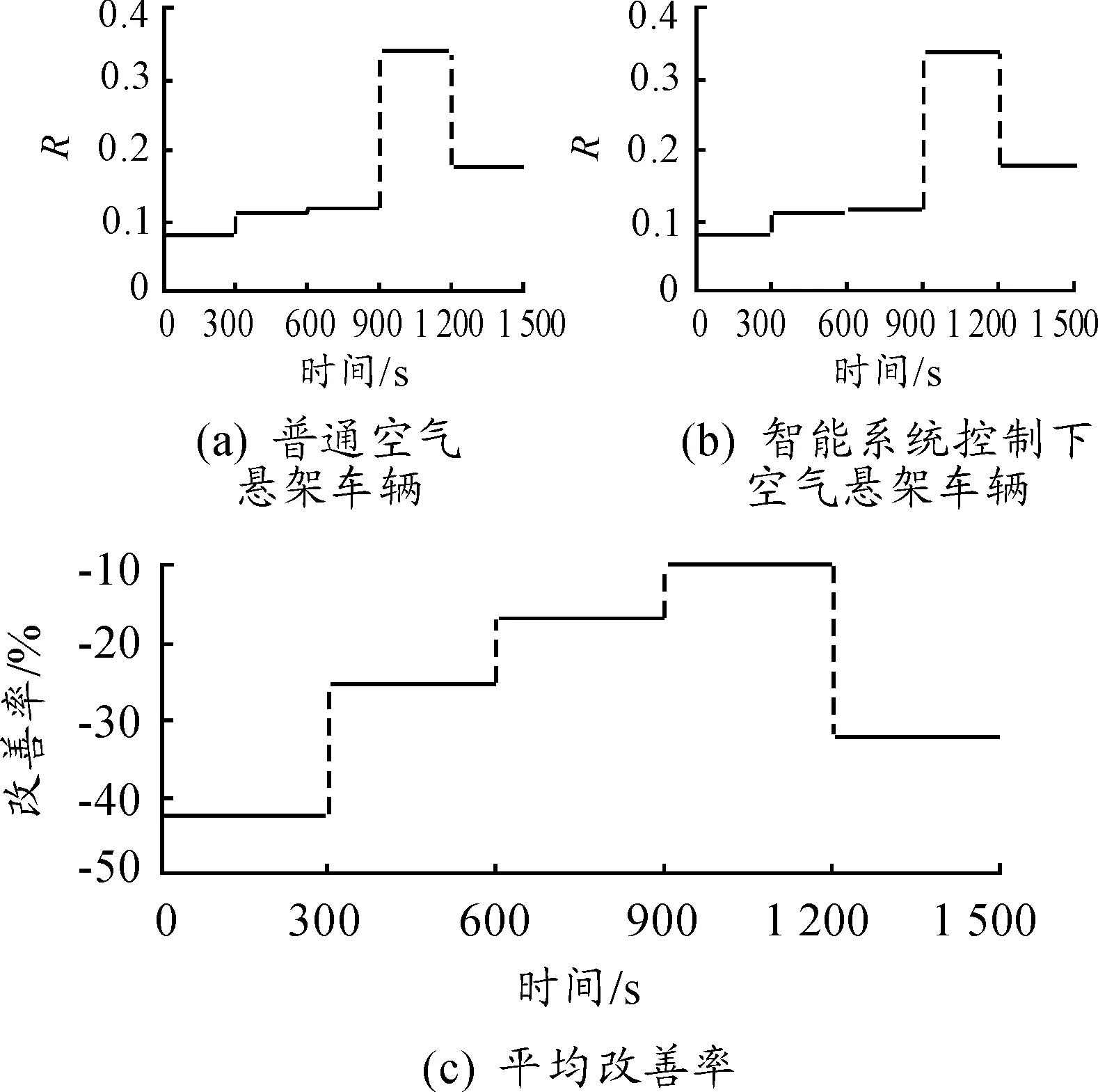
图16 不同工况下R的平均改善率

平顺性评价指标加权加速度均方根值aw/(m·s-2)传统空气悬架车辆aw0.580 7智能系统控制下空气悬架车辆aw0.583 3改善率/%0.45
表3 混合工况下操纵稳定性性的评价指标

操稳性评价指标侧倾因子R传统空气悬架车辆R0.213 4智能系统控制下空气悬架车辆R0.164 7改善率/%-22.82
根据图13、14可知:与传统空气悬架车辆相比,在智能系统控制下的车辆加权加速度均方根值的改善率在-0.4%~0.6%,侧倾因子的改善率在-20%~-45%。由图15、16可知:各个工况下的加权加速度均方根值的平均改善率在-1%~2%,侧倾因子的平均改善率在-10%~-50%。从表2、3可知:在整个仿真过程中,在智能系统控制下的车辆行驶平顺性略有降低,加权加速度均方根值升高了0.45%,操纵稳定性提升较大,侧倾因子下降了22.82%。结果表明:在车身高度智能控制系统的控制下,可以在不恶化行驶平顺性的同时提高车辆的操纵稳定性。
4 结束语
基于智能体理论,结合传统车身高度调节系统设计了车身高度智能控制系统。该系统可以通过感知行车过程中获得的外界信息,通过在线学习完善自身知识库,并基于知识库以及行驶工况信息自适应地调整车身高度。
单一工况下的学习结果证明了智能体学习行为的有效性与适用性。通过不同学习算法间的仿真对比,证明了通过汤普森抽样算法构建的智能体学习行为更加高效实用。在混合工况下进行仿真,验证了车身高度智能控制系统的控制效果,与传统空气悬架车辆相比,簧载质量加权加速度均方根值上升了0.45%,侧倾因子下降了22.82%。
下一步的研究将考虑车身高度与阻尼、互联状态的协同控制,使得空气悬架车辆可以获得更好的动态性能。

