分数阶磁流体方程组的一些研究进展

周 勇,朱铭旋

(1.中山大学， 广东 珠海 519082； 2.嘉兴学院， 浙江 嘉兴 314001)

1 相关研究进展

本文主要讨论的是分数阶磁流体方程组，其具体形式如下：

(1)

Wu[21]用Galerkin逼近的方法得到全局存在的弱解，其弱解定义为:如果向量函数(u,b)满足以下条件：

①u∈L∞(0,T;L2)∩L2(0,T;Hα)

b∈L∞(0,T;L2)∩L2(0,T;Hβ)

那么，称(u,b)是方程(1)的一个弱解。

近期，Jiang和Zhou[12]证明了广义磁场流体方程组(1)强解的局部适定性，具体如下：

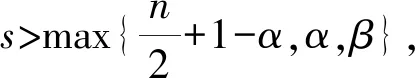
u∈C(0,T*;Hs(Rn))∩L2(0,T*;Hs+α(Rn))

b∈C(0,T*;Hs(Rn))∩L2(0,T*;Hs+β(Rn))

当s≥2时，

u∈C(0,T*;Hs(Rn))∩C1(0,T*;Hs+α-2(Rn))

b∈C(0,T*;Hs(Rn))∩C1(0,T*;Hs+β-2(Rn))

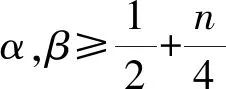
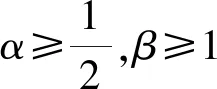
(2)

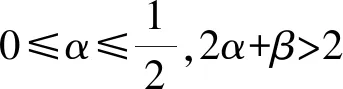
(3)

③α≥2，β=0

(4)

基于其结论，很多数学工作者做了一定的改进[1,4,11,15,16,23-25,29,31]。Zhou等[4]将式(2)改进至

α>0,β=1

(5)

Jiu等[15]将式(3)改进至

α=0，β>1

(6)

三维时，Zhou[33]对α，β≥1时建立了下列正则性准则：

或者

2 一些公开问题

下面提出两个公开问题：

1) 对于二维情况下式(1)存在整体解的条件，现在最优的是如下4种情况：

①α≥2,β=0;

②α>0,β=1；

③α=0，β>1;

④β∈(0,1),α+β≥2。

能否将指标进一步降低，是该领域关注的热点问题。猜测当α+β≥1时，分数阶磁流体方程组整体解存在。当前阶段该猜测有较大的难度，α+2β≥2是值得尝试的问题。

2) 当不考虑磁场的影响，式(1)退化为分数阶Navier-Stokes方程组。

ut+u·▽u+▽P+vΛ2αu=0,

divu=0