PC准则下线性无偏估计的比较
李 勇,邬吉波
(重庆文理学院, 重庆 402160)
通常采用均方误差矩阵准则和均方误差矩阵来比较估计的优良性。Rao[1]指出在一些情况下运用均方误差以及均方误差矩阵准则来比较估计是不合理的,而运用Pitman准则[2]能更好地度量估计的优劣性。有学者研究了PC准则,如Wang and Yang[3],Yang等[4],Jozani[5],Wu[6]等。
有学者研究了PC 准则下线性估计的比较。如Mason等[7]给出了2个线性估计在PC准则下的比较,同时给出了一个估计优于另一个估计的条件。但是,Mason等提出的定理不好用,Yan[8]对Mason等提出的定理进行了改进。Fountain等[9]讨论了2个线性无偏估计在PC准则下的比较,同时得出了比较完美的结果。但是Fountain和Keating的结果只针对线性无偏估计,有其局限性。本文针对非线性的情况,讨论2个无偏估计在PC准则下的比较,不管是线性还是非线性。本文的结果表明:对2个无偏估计,如果某一个估计的协方差矩阵越小,则此无偏估计在PC准则下越好。
1 主要结果
首先给出PC准则的定义:


下面给出本文的主要定理:

证明:由定义2.1,取Q=I,我们有
(1)
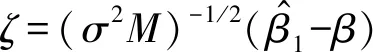

Pr{ζ′Mζ-η′Mη-η′(N-M)η≤0}≥
Pr{ζ′Mζ-η′Mη≤0}
(2)
由于M是一个正定矩阵,则存在一个正交矩阵使得:
M=H′ΛH,Λ=diag(λ1,λ2,…,λp)
其中λ1≥λ2≥…≥λp是M的特征值。

(3)
下面计算
(4)

Pr{δ2′Λδ2-δ1′Λδ1≤0}
(5)
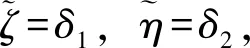
Pr{δ1′Λδ1-δ2′Λδ2≤0}
(6)
由式(4)~(6)有
Pr{δ2′Λδ2-δ1′Λδ1≤0}=
Pr{δ1′Λδ1-δ2′Λδ2≤0}=
1-Pr{δ1′Λδ1-δ2′Λδ2≥0}
(7)
所以




2 应用
2.1 一般线性模型
考虑如下的模型:
Y=Xβ+ε
(8)
其中:Y为观测矩阵;X为已知的设计矩阵;β为未知参数向量;ε为误差向量且E(ε)=0,Cov(ε)=σ2V,V>0。
模型(8)的最小二乘估计为
(9)


2.2 带线性约束的线性模型
考虑模型(8)以及V=I,未知参数满足如下的约束条件:
Rβ=r
其中:R是一个已知的矩阵;r为一个向量。则未知参数的约束最小二乘估计为
计算得到
以及
σ2(X′X)-1R′[R(X′X)-1R′]-1R(X′X)-1
易知
则有

2.3 带随机约束的线性模型
考虑模型(8)以及V=I,未知参数满足如下的约束条件
r=Rβ+e,e~(0,σ2W)
其中:R是一个已知的矩阵;r为一个向量。则未知参数的混合估计为
那么



