根据目标信息，巧解数学问题

☉山东省济南市莱芜区雪野镇中心中学 许迎新

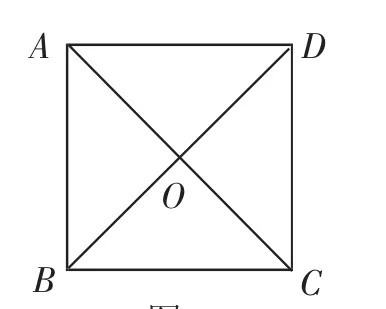
图1

在我们解决数学问题时，总要根据数学问题蕴含的解题信息才能求解.当然，很多时候数学问题蕴含的解题信息往往不止一个，甚至是多个解题信息.例如，如图1，正方形ABCD的边长为1，对角线AC、BD相交于点O，求OC的长.在这个问题中，就蕴含很多解题信息.如数量关系方面的信息：AB=BC=CD=AD=1，OA=OB=OC=OD，∠ABC=∠BCD=∠CDA=∠DAB=90°，对角线AC平分∠DAB和∠BCD，对角线BD平分∠ABC和∠ADC；位置方面的关系：AB∥CD，AD∥BC，对角线AC与BD互相垂直平分，△AOB、△BOC、△COD、△AOD、△ABC、△BCD、△CDA、△DAB都是等腰直角三角形.在众多的解题信息中，我们可能只用到部分解题信息.而且不同的人由于使用的解法不一样，因而用到的解题信息也不尽相同.再如化简这个式子中包含的解题信息有无论是数与式，还是几何图形或函数图像，都蕴含有解题信息.而我们把那些与解题目标最为密切的解题信息称为目标信息.下面举例说明在解决数学问题时如何利用目标信息使数学问题获得巧解.

一、巧用式中的数量关系

许多代数式都蕴含很多解题信息.我们可以通过作和、差、倍、分，甚至平方和、平方差等多种手段对代数式进行处理，以便发现这些代数式中蕴含的解题信息，然后选取与解题目标关系最密切的信息，从而使问题便捷求解.

例1解方程（x-2）（x-5）=-2.

本题若按常规解法，只需把原方程化为一元二次方程的一般形式x2-7x+12=0，然后对左边进行因式分解，得（x-3）（x-4）=0.则x-3=0或x-4=0.则原方程的解为x1=3，x2=4.仔细观察原方程等号左边，我们发现两个因式x-2与x-5正好相差3，即（x-2）-（x-5）=3，而右边的-2正好可以分成两个相差3的数相乘，即-2=1×（-2）=2×（-1），因此必有x-2=1（或x-5=-2），或者x-2=2（或x-5=-1）.则x=3或x=4.这样也可以求出原方程的解为x1=3，x2=4.这种解法不需要对原方程进行化简整理，不需要进行因式分解，而只需进行因数分解，大大减少了运算量，甚至可以口算，不得不说这是一种在认识观察方程结构的基础上得出的巧妙解法，更是一种创新解法，确实是“化腐朽为神奇”！

二、巧对常数进行变形

我们知道，当一元二次方程ax2+bx+c=0（a≠0）的判别式大于0时，一元二次方程有两个不相等的实数根.反之，若则x1、x2又可以看作一元二次方程的两不相等实根，这实际上是对一元二次方程根的定义的逆向应用.在逆向应用一元二次方程根的定义时要注意观察所给方程的结构特征是否具有或者可以化成和的形式.

本题若按常规方法，可以先对原方程组进行整理，即将原方程组化成整系数方程，得然后解方程组，这样做本身无可厚非.如果仔细观察方程组中的两个方程，我们发现，若将36化成62，将49化成72，原方程组可以化成的形式，这样两个方程都具有的结构，逆用一元二次方程根的定义可知和是一元二次方程xp2-yp+1=0的两根.由一元二次方程根与系数的关系定理，得则这样我们把一个看似与一元二次方程无关的方程组问题，通过对方程组中的方程变形，巧妙地利用一元二次方程的知识求解，得到了本题的创新解法，极大地开阔了学生的视野，开拓了学生的思维能力.

三、巧用已知条件和待求结论之间的倍分关系

在列方程解决实际问题时，一般情况下，我们都是根据能够表示全部数量关系的相等关系列方程求解.但在某些情况下，如果直接根据相等关系列方程，思路虽然简单，方程也容易列出，但由于所列方程比较繁杂，无疑增加了求解困难和运算量，此时我们可以对相等关系进行变通，或者另外寻求突破口，使问题的求解变得相对简单.

例3如图2，在矩形ABCD中，AB=20厘米，BC=16厘米，动点M从点A出发沿AB以4厘米/秒的速度向终点B运动，同时动点N从点B出发沿BC以2厘米/秒的速度向终点C运动，它们到达终点后停止运动.几秒后，点M、D之间的距离是点M、N之间的距离的2倍？

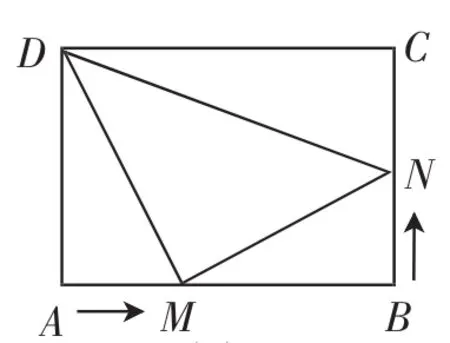
图2

假设t秒后，点M、D之间的距离是点M、N之间的距离的2倍.此时AM=4t，BM=20-4t，BN=2t.在Rt△ADM中，由勾股定理，得在Rt△BMN中，由勾股定理，得根据“点M、D之间的距离是点M、N之间的距离的2倍”列方程得这是一个无理方程，求解比较困难.注意到点M的运动速度是点N的运动速度的2倍，因此AM=2BN，而点M、D之间的距离是点M、N之间的距离的2倍意即DM=2MN.则而且△ADM和△BMN都是直角三角形，根据“斜边、直角边”可知△ADM △BMN.则.即，即解得t=3.不难看出，由于我们对“点M、D之间的距离是点M、N之间的距离的2倍”这个可以列方程的等量关系进行转换，转化成“△ADM △BMN”，所列方程简单多了.

以上我们谈了如何根据目标信息解决一些数学问题.这样的例子还有很多，如已知方程组的值。常规方法是先求出方程组的解然后再计算x+y的值。事实上，由于我们要求的是x+y的值，也可以先将x+y从两个方程中分离出来，即将方程组转化为（Ⅰ）的形式，在方程组（Ⅰ）中，由②-①×2，不难求出x+y=20；在方程组（Ⅱ）中，由①×4-②，得3（x+y）=60，所以x+y=20.再如已知方程组求x+y的值，我们就没有必要求出方程组的解，而是直接将两个方程的左右两边相加，可得，即这样很容易求出x+y=9.9。再如，在四边形ABCD中，对角线AC、BD相交于点O，DA=DB=DC，如图3所示. 如果∠CAB=2∠ACB，且∠ADB=46°，你能求出∠BDC的度数吗？对于该题，如果利用常规方法，需要根据等腰三角形的性质和三角形内角和定理求解，运算量大，比较麻烦.如果能够注意到“DA=DB=DC”这个条件，联想到圆的定义，不难断定点A、B、C都在以点D为圆心的圆上，因此可以通过构造辅助圆（如图4）求解，这样就简单多了.希望学生在今后的学习中多加总结，注意根据目标信息对数学问题进行巧妙求解，提高解题效率，让解法“大放光彩”.

图3

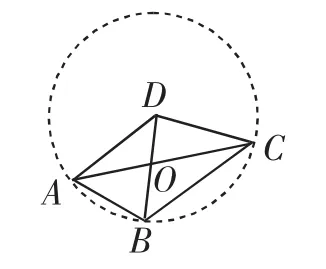
图4