弯剪破坏钢筋混凝土桥墩的变形能力分析
赵锦平,马 颖,石程程,2
(1.华北水利水电大学水利学院,河南 郑州 450046;2. 北京交通大学土木建筑工程学院,北京 100044)
钢筋混凝土桥墩作为桥梁结构的重要竖向承重和水平抗力构件,在地震荷载作用下一旦破坏会影响结构的整体稳定,而稳定性分析是结构安全评估的重要内容之一[1- 3]。随着基于性能/位移抗震设计理论的发展,国内外对结构抗震问题的研究由原来单纯的强度抗震思想逐步向延性抗震设计理论发展,使结构满足变形能力要求,降低对其强度的要求。钢筋混凝土桥墩的破坏主要有弯曲破坏、剪切破坏或弯剪破坏。部分结构基于位移的抗震设计和修复规范强调[4- 7],墩柱的弯曲性能和端部塑性(转动)变形能力相关,而脆性剪切破坏必须严格控制。我国现行规范中钢筋混凝土桥墩的变形能力研究主要针对弯曲破坏模式,而对弯剪破坏的情况考虑甚少。弯剪破坏是介于弯曲破坏和剪切破坏之间的一种破坏模式,具有有限的变形和耗能能力,历次地震均有发生。因此,有必要研究弯剪破坏模式下钢筋混凝土桥墩的变形能力。
目前研究表明位移延性系数作为桥墩变形能力指标之一,其受桥墩高度(剪跨比)的影响较大,采用塑性铰区曲率延性系数作为桥墩变形能力指标更为合理,其次是桥墩极限位移角。孙治国等[8]分析表明对于不同的剪跨比,极限位移角和曲率延性系数两者作为桥墩变形能力指标具有较好的一致性;并且考虑了轴压比、配箍率、纵筋配筋率、混凝土和钢筋强度等的影响,建立了弯曲破坏墩柱极限位移角回归公式。
本文整理美国PEER柱抗震性能试验数据库中发生弯剪破坏的20根矩形截面RC墩柱的拟静力试验数据,识别屈服位移角和极限位移角作为桥墩变形能力量化指标,分析其主要影响因素,并建立各影响因素与屈服和极限位移角之间的关系。
1 弯剪破坏桥墩试件试验数据
本文借助美国PEER柱抗震性能试验数据库,整理了20根矩形截面钢筋混凝土墩柱试件的拟静力试验数据进行分析,均为弯剪破坏。PEER数据库中对钢筋混凝土墩柱发生弯剪破坏的界定条件是:在试验过程中出现剪切裂缝,并且有效荷载下降到80%时对应的破坏位移延性μfail>2,或Feff(最大有效荷载的绝对值)≥0.95F0.004(受压区混凝土达到极限压应变0.004所对应的荷载)。PEER数据库提供了每根钢筋混凝土墩柱试件的几何尺寸、材料特性、加载条件、荷载-位移曲线和破坏模式。试件参数见表1,21MPa≤混凝土圆柱体抗压强度fc′≤86MPa;330.96MPa≤纵筋屈服强度fyl≤510MPa;316MPa≤箍筋屈服强度fyv≤559MPa;1.27%≤纵筋配筋率ρl≤3.03%;0.07%≤箍筋面积配箍率ρv≤1.19%;0.07≤轴压比n(=P/Agfc′)≤0.9;1.5≤剪跨比λ(=a/h)≤3.22。其中,P为轴向荷载,a为剪跨,h为截面高度。
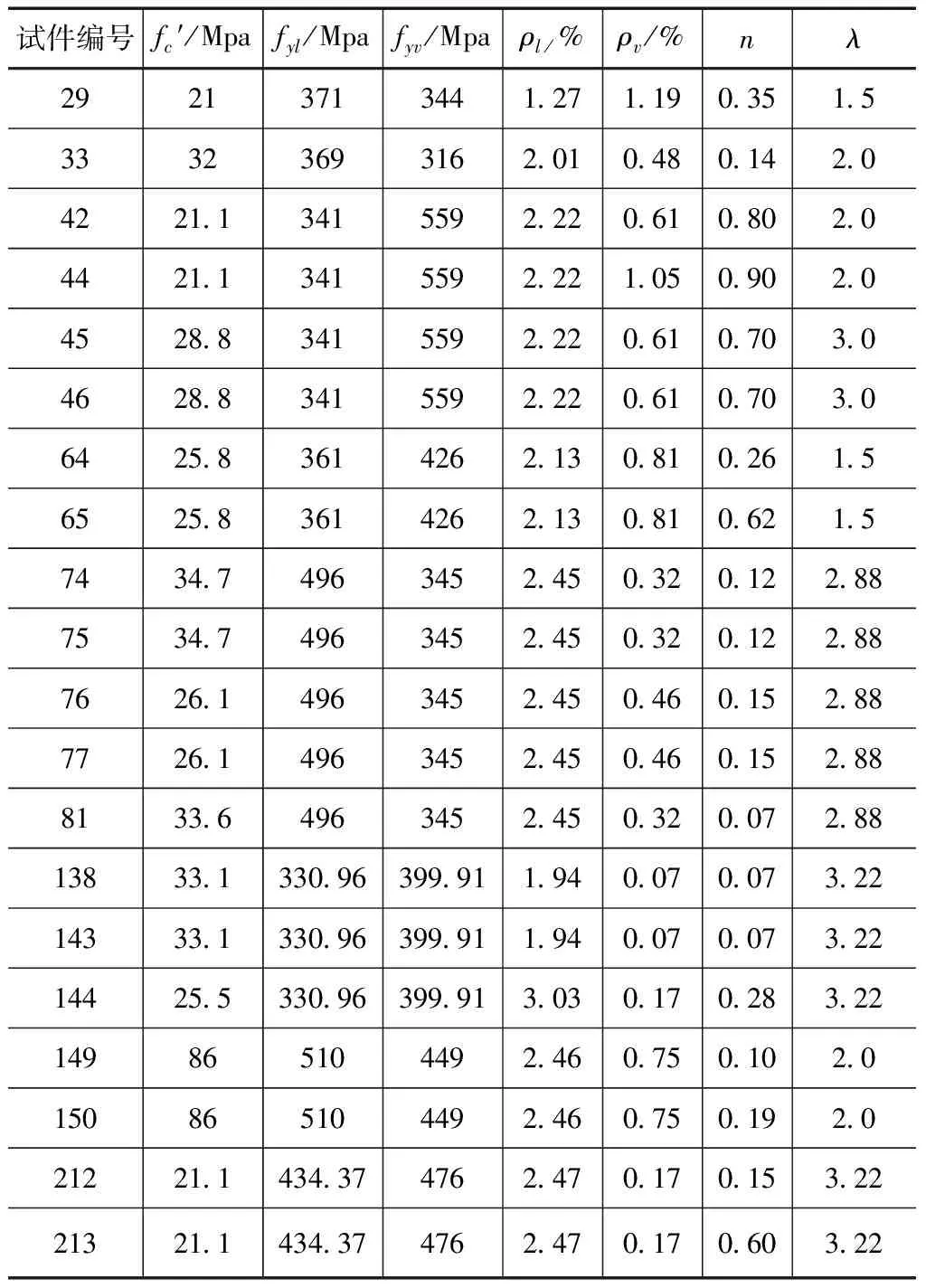
表1 弯剪破坏墩柱试件参数
2 弯剪破坏桥墩试件变形能力识别
对于弯剪破坏桥墩,只要变形能力达到相应的评价标准,工程即是可以接受的。桥墩的变形能力越大,其吸收和消耗地震能量的能力越强,抗震性能越好。PEER数据库仅提供了荷载-位移曲线,需要识别发生弯剪破坏桥墩的变形能力。本文将以桥墩的屈服位移角δy和极限位移角δu评价桥墩的变形能力:
(1)
式中,Δy、Δu—分别为墩柱顶屈服位移和极限位移;L为墩柱高度。
确定屈服位移的方法通常有三种:屈服弯矩法、能量等值法和Park建议的方法。本文弯剪破坏钢筋混凝土桥墩的屈服位移识别采用Park建议的方法:通过原点(0,0)和骨架曲线正负方向上(0.75F±max,D)射线上F±max对应的位移值Δ±y,取其平均值为屈服位移,即Δy=(︱Δ+y︱+︱Δ-y︱)/2。
弯剪破坏钢筋混凝土桥墩的极限位移识别方法[9]:在同一位移幅值Δ下,若末次水平荷载(一般循环次数大于等于3)小于同位移幅值下最大荷载值的85%时,即FΔ,end≤0.85FΔ,max,则定义首次施加位移幅值Δ所对应的水平荷载为弯剪破坏墩柱试件的抗剪强度,与其对应的位移为极限位移Δu。墩柱试件滞回曲线、骨架曲线、Δy和Δu识别如图1所示,然后按式(1)计算其屈服位移角和极限位移角。

图1 弯剪破坏墩柱试件Δy和Δu识别
3 弯剪破坏桥墩变形能力分析
影响钢筋混凝土桥墩变形能力的因素主要有剪跨比、轴压比、配箍率、纵筋配筋率、混凝土和钢筋强度等。本文主要研究剪跨比、轴压比、配箍率、纵筋配筋率的影响。
3.1 剪跨比
剪跨比反映了构件截面承受弯矩和剪力的相对大小,即正应力和剪应力的相对关系,影响了墩柱的破坏模式和变形能力。研究表明[10],剪跨比较小的短柱或极短柱,通常发生脆性剪切破坏,塑形变形能力较差;而剪跨比较大的长柱,往往发生弯曲破坏,具有较好的侧向变形能力。
Davey和Park[11]曾对不同剪跨比墩柱进行试验研究,结果表明墩柱的变形能力随着剪跨比的增大而增大;美国国家标准技术研究所的研究表明[12],剪跨比为3和6的足尺墩柱均发生弯曲破坏,随着剪跨比的增大,塑性铰长度增大,变形能力增强。
图2示出墩柱屈服位移角δy和极限位移角δu随着剪跨比λ的变化,可以看出,随着剪跨比的增加,墩柱的屈服和极限位移角总体的趋势是增大的,说明弯剪破坏桥墩的侧向变形能力随着剪跨比的增大而逐渐增大。通过回归分析,建立墩柱的屈服和极限位移角与剪跨比的关系,公式中指数和系数均为正数,说明墩柱的屈服和极限位移角与剪跨比正相关。发生弯剪破坏桥墩的剪跨比大多在1.5~3之间,由于剪跨比变化范围不大,收集的试验数据有限,位移角变化规律不是特别明显。

图2 剪跨比与位移角的关系
3.2 轴压比
轴压比是影响墩柱变形能力的另一重要因素。Sheikh[13]的试验研究认为,高轴压作用下墩柱的变形能力降低;东洋一等的试验研究[14]也表明轴压比大于0.3的墩柱试件的变形能力随轴力增大而迅速下降,应对轴压比进行限制,通过增设横向钢筋的方法效果甚微;张明等[15]的研究结果也表明,随着轴压比的增大,裂缝宽度增大,墩柱的侧向变形下降显著,压区混凝土破坏严重。
墩柱屈服位移角δy和极限位移角δu随着轴压比n的变化示于图3。由图3可以看出,随着轴压比的增大,墩柱屈服和极限位移角降低明显,尤其极限位移角降低更为显著,这一规律也在极限位移角与轴压比的回归公式具有较大的斜率中体现出来。另外,回归公式的斜率均为负数,说明墩柱屈服和极限位移角与轴压比负相关。
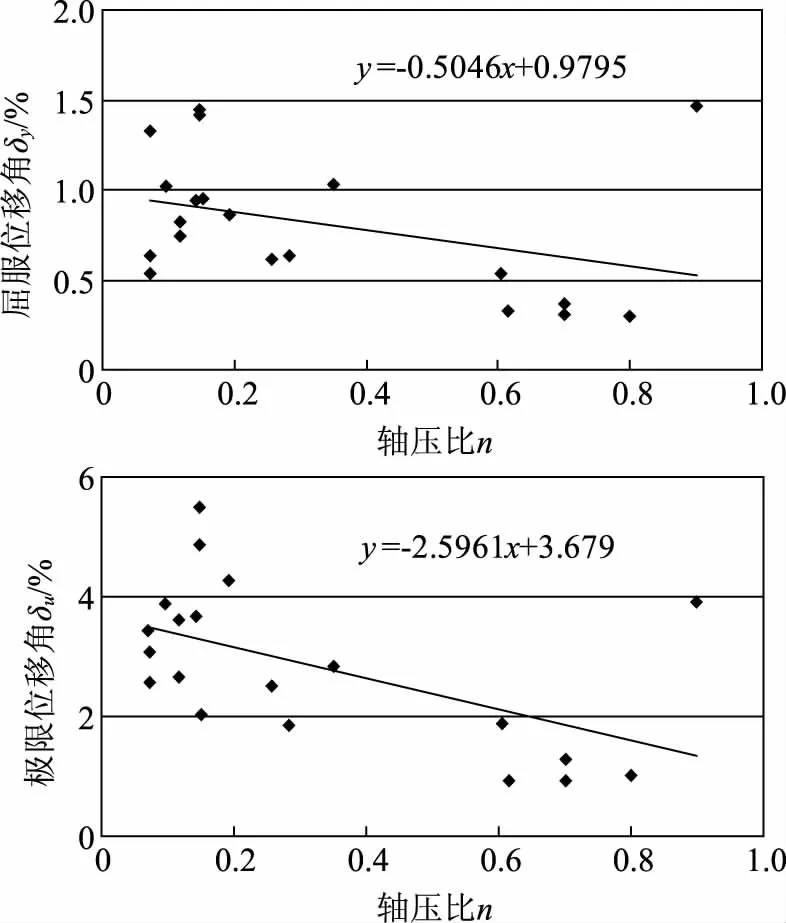
图3 轴压比与位移角的关系
3.3 配箍率
大量的试验研究表明[16- 17],箍筋配置增多可以增大桥墩的抗剪强度,防止脆性剪切破坏;而且能够限制斜裂缝的宽度及发展,对核心混凝土提供有效约束,使混凝土极限压应变得到提高,延缓混凝土压碎破坏过程;同时对纵筋提供有效约束,增大纵筋的抗屈曲能力;从而增大了钢筋混凝土桥墩的变形能力。
墩柱屈服位移角δy和极限位移角δu随着配箍率ρv的变化及其建立的关系如图4所示,可以看出,墩柱位移角δy和δu均随着配箍率ρv的增大而增大。位移角回归公式的斜率均为正数,说明墩柱屈服和极限位移角与配箍率正相关,说明配箍量的增大和箍筋间距的减小可以有效提高墩柱的变形能力。并且,墩柱极限位移角公式的斜率0.211大于屈服位移角公式的斜率0.1902,说明增加配箍率对极限位移角增大的影响更明显。
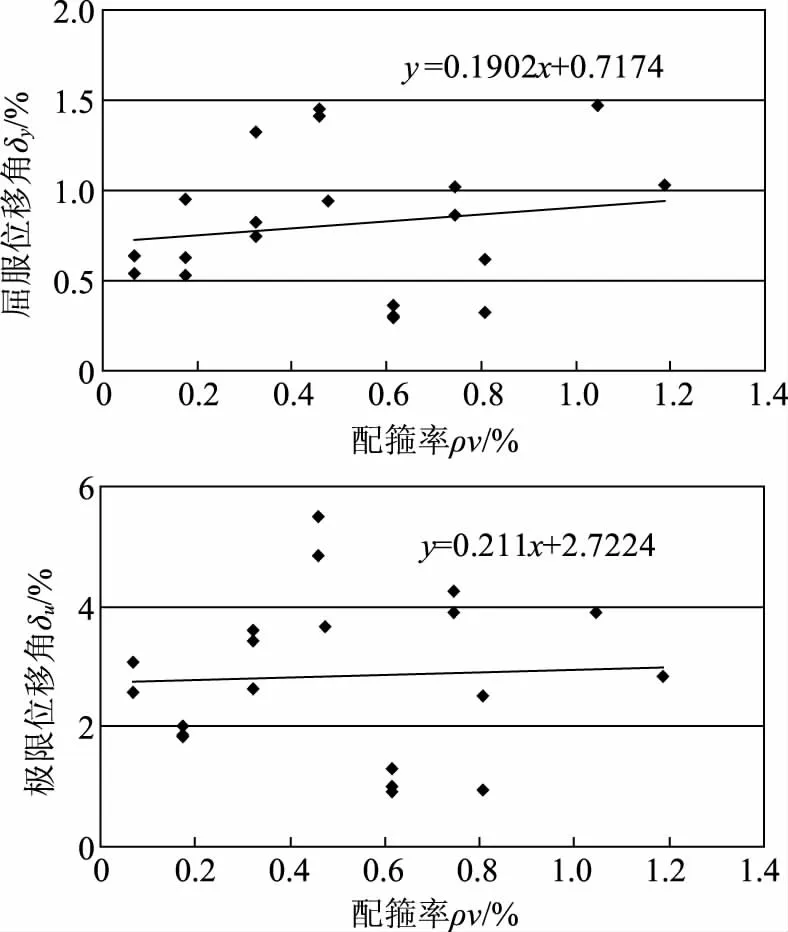
图4 配箍率与位移角的关系
3.4 纵筋配筋率
大量的试验数据与研究结果表明[18],桥墩的变形能力会随着钢筋混凝土核心区的纵筋配筋率的增加而增强,但随着纵筋配筋率的增大,轴压比通常会提高,过高的轴压比会削弱结构的变形能力,所以纵筋配筋率也存在限值。
墩柱屈服位移角δy和极限位移角δu随着纵筋配筋率ρl的变化规律及其建立的关系如图5所示。纵筋配筋率ρl在1~2.5范围内,随其增大,墩柱的位移角δy和δu均增大。位移角回归公式的斜率均为正数,说明墩柱屈服和极限位移角与纵筋配筋率正相关。并且,墩柱极限位移角公式的斜率0.3324大于屈服位移角公式的斜率0.1003,说明增加纵筋配筋率对极限位移角增大的影响更明显。值得注意的是,ρl增大到3.03%时,位移角δy和δu反而均减小,说明纵筋配筋率存在限值,一般不超过2.5%。

图5 纵筋配筋率与位移角的关系
总体而言,为了提高弯剪破坏桥墩的变形能力,可以增大剪跨比λ、面积配箍率ρv、纵筋配筋率ρl或降低轴压比n。对比剪跨比λ、轴压比n、面积配箍率ρv和纵筋配筋率ρl与位移角δy和δu之间建立的公式可以看出,轴压比n与位移角δy和δu公式的斜率最大,说明轴压比对弯剪破坏墩柱变形能力的影响最大。
应当指出,本文建立的各影响因素与位移角之间的公式存在两方面不足:一是试件数量仍显少;二是此关系仅适用于分析弯剪破坏桥墩的变形能力,分析前需要判别桥墩的破坏模式,判别方式参考文献[19]。
4 结论
本文借助美国PEER数据库钢筋混凝土弯剪破坏墩柱拟静力试验数据,识别了桥墩的屈服和极限位移角,分析了影响其变化规律的主要因素,并建立各影响因素与屈服和极限位移角之间的关系。主要结论如下:
(1)随着剪跨比λ的增大、轴压比n的减小、面积配箍率ρv或纵筋配筋率ρl的增大,钢筋混凝土墩柱的屈服和极限位移角均增大,从而提高了弯剪破坏桥墩的变形能力。
(2)增大剪跨比λ、面积配箍率ρv、纵筋配筋率ρl或减小轴压比n对弯剪破坏墩柱极限位移角增大的效果更明显,对屈服位移角增大的效果稍小。
(3)轴压比n对弯剪破坏墩柱的屈服和极限位移角的影响最大。

