基于语言评价标准的大规模群体评价方法及应用

李贵清 李 红

(1.东北大学 中国改革发展研究院，辽宁 沈阳 110004；2.江西司法警官职业学院，江西 南昌 330013)

一、引言

随着社会经济的不断发展，人们活动越来越社会化。与之相应的人们在评价一些重要问题的时候，为了使其更加的公正、合理、客观，评价主体越来越倾向于群体化，由此形成群体评价。[1-14]然而，现实生活中由于评价主体在阅历、知识、素质、偏好等方面的个体差异，在评价过程中对被评价对象的评价结果自然也迥然相异，如何在多属性的群体中评价问题,尤其大规模群体评价问题中准确地描述群体中各个成员的意见和偏好，并将其集结成群体偏好是大规模群体评价的关键所在。

关于群体语言评价的研究一直是中外学者们研究的热点。目前常见的方法有基于模糊数的、聚类分析和基于二元语义等方法。[15-17]本文所提出的方法是基于语言评价标准的大规模群体评价方法。基于语言评价标准的分析方法一般先将评价者的评价信息转化为二元语义信息，再在此基础上将二元语义与其他信息集结方法相结合进行群体评价。[18-27]胡乐江等利用三角模糊数来表示评价者所给出语言评价信息的属性值及属性权重，并通过建立指标排序模型对评价信息进行集结。[28]张伟通过层次分析法(AHP)结合模糊理论形成模糊层次分析法(FAHP)来解决对群体偏好集结问题，该方法可以较好的模拟人类思维的模糊性，但是该方法较为复杂难以适用于大群体的偏好集结问题；[29]姜艳萍、樊治平利用二元语义对语言评价信息进行处理，结合传统的最大树聚类分析方法,针对多指标语言评价信息的聚类分析问题,提出了一种基于二元语义处理的最大树聚类方法；[30]张震、郭崇慧结合VIKOR方法，提出了一种基于二元语义信息处理的多属性群决策方法，该方法使用二元语义信息集结算子获得决策群组的相关信息，并利用最大化群效用和最小化个体损失来获取决策者满意的折衷方案，该方法可有效解决评价过程中信息丢失、扭曲等问题。[31]韩二东等提出利用二元语义加权算术平均TWAA算子集结转化后的判断矩阵，得出群体二元语义判断矩阵，并利用二元语义有序加权平均TOWA算子推算出某一方案优于其他所有方案的整体偏好程度，得出方案择优排序。[32]林健、金伟等学者提出利用二元语义结合特别定义的TOWA算子，来对群体的评价信息进行集结，进而对群体进行评价，此方法可以较有效地体现评价信息，但只是单纯通过算子来对群体方案进行集结，没有考虑到群体的偏好问题；[33-34]张爱萍、涂振坤将二元语义与层次分析法相结合，以此来确定出各个评价指标之间的权重关系，此方法可以得到较为准确的各评价指标的权重，但该方法只是横向的考虑评价指标，没有纵向考虑评价者的问题。[35]

在上述的研究成果中，对于语言类评价信息的研究大多是建立在对已有方法的优化及减少不确定性的基础上展开的，根据参与评价的专家对事先所制定的评价等级给出“好”或“差”等语言评价信息。但是，上述文献中对被评价者的评价分级标准并没有足够细化，对于“好”“较好”“很好”等评价语言间的界定也没有给出明确的标准。所以，评价者们不同标准所给出的评价结果而产生的不准确性将直接影响到最终结果的准确性。为此，本文首先制定了详细的语言评价分级标准，并结合二元语义对语言评价信息进行准确的量化，再从指标上对单一被评价对象的评价信息进行集结；同时，考虑到大规模群体评价中信息分布不均的问题，且一般的集结算子过程过于繁琐，适用性不强，因此本文通过定义信息一致的概念，利用信息一致度计算出各群体的密度权重，最后对评价者的结果进行纵向加权集结。相较于传统的群体评价方法，该方法综合考虑了评价者和评价指标，能够得到更为准确的语言评价信息，最大限度地减少由于评价者主观认知所带来的不确定性，评价信息更为准确可靠，并且具有简单易行的特点。最后，利用一个具体算例来进行实证说明。

二、语言评价标准及二元语义信息

(一)评价标准的制定

在已有的文献资料中，对于专家的评价标准很少进行统一，故此专家通常是根据自身已有的学识和经验对被评价对象进行判断。有些文献也会考虑到专家标准的不同，于是对专家给出的结果进行归一化处理。但是经过这样归一化处理后的结果都会有或多或少的信息损失，而且并没有从根本上解决专家标准不同的问题(当群体规模较大时，该问题便显得更为突出)。为了最大限度地保有专家结果的信息量，本文通过最开始制定出一个统一的评价标准，让所有专家按这个标准对被评价对象进行评价，由此可以最大限度地保证结果的客观性。为了让专家能够更加准确地判断各个方案间的不同，需要在专家进行评价之前，拟定出详细的评价标准。首先对于所给出的语言评价集必须合理，针对不同情况语言评价集会有不同。本文给出一般情况下的语言评价集，通过已有文献研究结果可以看出，事先给出的语言评价集S内的元素个数以七个为最佳。所以本文事先制定的语言评价集为S={s1=非常差，s2=很差，s3=差，s4=一般，s5=重要，s6=很重要，s7=非常重要}。为了使专家能够更加方便准确地给出评价结果，本文对语言评价集中的不同等级之间的界定拟定出更加细致的标准。

在日常研究中，人们拟对一个对象的等级进行描述时，常常需要借助另一个基础的等级去对它进行比较，例如当说一个物体5公斤，人们通常给出这个结果是基于这个物体与已知的1公斤的物体进行比较所得到的。也即是说，我们语言评价等级的给出需要一个参考值作为对比，这种情况下，人们可以让不同评价对象在同一评价指标下进行两两比较，以其中一个被评价对象为参考标准，以被评价对象在该指标下对最终结果所产生的效用为依据对另一个被评价对象进行评价。例如，A和B两个被评价对象在X评价指标下的比较，以A为参考标准，记A为“一般”，在只考虑X指标对最终结果的效用情况下，若B相较于A对最终结果的效用是A的1.5倍，则B应评为“很重要”。由于在现实的评价中很难去准确地判断出两个方案在某个指标下对最终结果的效用的倍数关系，所以这里给出的倍数是一个大概的模糊参考值。下面给出不同评价等级(相对于“一般”等级而言)效用倍数的区间。

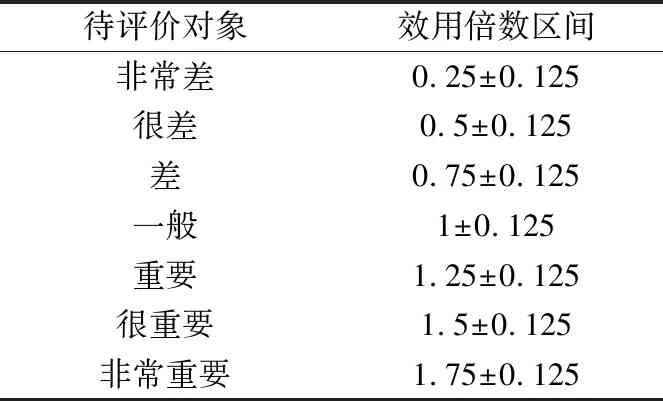
表1 不同评价等级的效用倍数区间

(二)二元语义信息

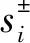
定义1：假定si∈S中的一个语言评价短语，那么其相应的二元语义形式可以通过下面的函数得到：[7]

θ∶S→S×[-0.5,0.5]

θ(si)=(si,0),si∈S

(1)

为了能够得到更加准确的结果，本文考虑到二元语义偏差下的评价，当评价分级较模糊时，可以通过下面定义的函数得到相应的二元语义形式。

(2)

定义3：设实数β∈[0,T]是语言评价集经过某种集结方法所得到的实数，其中，T为语言评价集S中元素的个数，则β可通过下面的函数Δ来表示二元语义信息：[7]

(3)

其中，round是“四舍五入”取整算子。

定义4：若(si,αi)是一个二元语义，其中si∈S，α∈[-0.5,0.5]则存在一个逆函数Δ-1使其可以转换成相应的数值β∈[0,T]：[6](P26-29)

(4)

三、二元语义指标信息横向集结

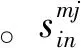
矩阵满足：

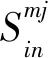
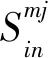
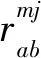
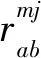
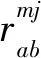
(5)

式中，T为S集合中的元素个数。

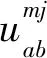
(6)

其中，locate(m)为M在矩阵中的位置。

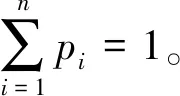
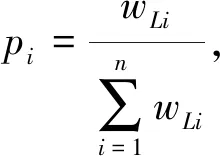
由定理可知，各个指标下的所有评价对象的量化值之和都是相等的，所以在各指标已知的情况下，通过此方法来得到的所有量化值都是合理的。

由于所有得到的量化值都是小于1的小数，所以我们需要对其进行标准化，再转化成为量化后的二元语义形式。

对于量化值P=(p1,p2,…,pn)，定义标准量化值β=(β1,β2,…,βn)，其中：

(7)

式中，T为S集合中的元素个数。

通过这种方法可以得到在某一个指标下的各个方案标准量化值，同理利用此方法可以得到所有指标下的各个方案的标准量化值矩阵βm，即：

然后在已知各个指标的权重值λ=[λ1,λ2,…,λj]的情况下，利用一般加权算子对被评价对象在各指标下的标准量化值(β)进行横向的集结得到该被评价对象的总体评价量化值(q)，进而求出所有专家对各个被评价对象总体评价量化值，具体步骤如下：

(1)对被评价对象在各指标下的标准量化值(β)进行横向集结得到评价对象的总体评价量化值(q)，即：

qi=λ1βi1+λ2βi2+…+λjβij

(2)同理，可以求出一个专家对所有被评价对象的总体评价量化值q，即：

q=[q1,q2,…,qn]

(3)求得所有专家对所有被评价对象的总体评价量化值的矩阵，得到所有专家(m)与所有被评价对象(n)的总体评价量化值矩阵Q，即：

四、群体信息纵向集结

在处理群体评价，尤其大规模群体评价时，一方面要注意尽量保持被评价对象间的差别，以便于对各个方案进行排序，另一方面要尽量得出让群体都可以接受的一致性结果。所以本文根据各专家的排序结果对大规模专家进行分组，然后以各组组内专家评价结果间的相似程度为依据求出组间的密度权重，最后利用密度权重将群体评价信息进行纵向集结。该方法既保留了各评价对象间的差别，又可以综合专家群体的整体意见，得出群体均可接受的结果。

(一)群体内部聚类及信息一致度

在所有的专家中，尽管各个专家之间的量化值会有所不同，但是由于问题所需要的结果只是所有被评价对象的排序或是最优，所以依然存在一部分的专家的最终结论是相同的。根据这个特征，可以对专家群体进行内部聚类。利用总体评价量化值的矩阵Q，得到各个专家对被评价对象的最终排序结果，于是存在t个不同的排序结果，然后将排序结果相同的专家分为同一组，于是会有t个组。

由分组依据可知，同一组内的专家的最终排序结果是一致的，然而同组内不同专家的量化值在很多情况下是不同的，为此需要分析出组内信息的一致性程度。

定义6：已知同组的专家的量化值Q=[Q1,Q2,…,Qc]，定义组内信息一致度σ，则有：

(8)

其中，Qc=[q1,q2,…qn]T,n表示被评价对象数，c表示组内专家数。从定义的公式可以看出，信息一致度表示的是同组专家的评价信息的相似性程度。

(二)群体密度权重的确定

根据专家的总体量化值，将群体评价信息进行纵向集结，其中每个专家的量化值可以由二元语义信息横向集结方法得到的量化值矩阵给出。因为每个专家所给出的评价信息都至关重要，所以设定各专家权重均相等，这样也更加容易得到专家们均认同的结果。此时群体密度权重确定的科学性便至关重要。群体密度反映的是群体信息的疏密程度。由于信息越密集其一致度越大，信息越稀疏其一致度越小，根据这种特性本文利用组内信息的一致度来确定出群体的密度权重。

已知各组的信息一致度σ=[σ1,σ2,…σt]，定义群体密度权重φ，则有：

(9)

然后对每个组别进行简单加权集结得到最终结果ξ，则有：

(10)

即ξ=[ξ1,ξ2,…ξn]为最终的群体评价结果向量，根据此结果可以对群体进行排序或者选最优。

下面给出基于语言评价标准的群体评价方法的具体步骤：

步骤1：专家事先制定出相应的语言评价标准。

步骤2：依据事先制定的评价标准体系，利用二元语义对各个被评价对象的各个指标进行两两比较，并给出评价分级，根据式(6)和式(7)对大规模专家给出的语言评价信息进行量化处理，得到被评价对象与指标的标准量化值矩阵，记为βm。

步骤3：对被评价对象在各指标下的标准量化值(β)进行横向集结得到专家对被评价对象的总体评价量化值，集结所有专家信息，得到关于专家与被评价对象的总体评价量化值矩阵Q。

步骤4：根据大规模专家的结论一致性进行分组，得到t个意见组。

步骤5：计算组的信息一致度。根据式(8)计算出各个组的信息一致度，得到各组的信息一致度σ。

步骤6：计算各组的群体密度权重。根据求得的各组信息一致度σ，由定义式(9)可求得各组的群体密度权重φ。

步骤7：将所有专家关于被评价对象的量化值根据群体密度权重进行纵向的集结，得到最终的决策结果。

五、算例验证

社会治安服务作为一项公共服务，是为维护社会公共秩序的安宁有序而由政府、市场和社会组织提供的服务，[36]具体来说就是政府、市场和社会组织针对破坏社会公共秩序行为产生的诱发因素、外部条件所进行的预防活动和针对该行为本身所进行的制止和打击活动，包括对破坏社会公共秩序行为的预防、制止和打击活动，以及对因破坏社会公共秩序行为陷于危难或困难境地或其他原因而处于危难境地的公众给予的救助活动。平安是最大的民生、治安是最大的环境，故社会治安服务的作用非常重要，其不但为社会成员的个人发展提供必不可少的外部环境，也为社会发展提供重要保障。为促进社会治安服务的有效供给，人们常常需要对社会治安服务进行评价，这也是当前治安学界关注的热点内容。[37-39]但由于社会治安服务评价是一个系统复杂的过程，对社会治安服务评价方法探讨也是当前有关学者热议焦点之一，如何为现实的评价提供一种简便有效的方法便显得非常有必要。本文拟以基于语言评价标准的大规模群体评价为方法，对江西省鄱阳湖区的五个县(区)的社会治安服务为对象进行综合评价，具体评价过程如下：

首先明确评价的相关背景。评价主体是由20名理论部门和实践部门的权威专家及业务骨干共同组成的评价小组；评价的对象是江西省鄱阳湖沿湖的五个治安较为复杂的重点县(区) (o)；项目评价指标分四个：成本分担类指标(x1)，投入产出类指标(x2)，满意度类指标(x3)和自由度感知类指标(x4)。为不失一般性，假设各指标重要性假设相同，即指标权重λ=[0.25,0.25,0.25,0.25]。

(1)依据本文所给出的评价标准体系对照表1对各个方案的四个指标进行评价，由于数据较多,本文不一一列举评价过程，仅以其中第一位专家为例，结果见表2。

表2专家一的语言评价信息表

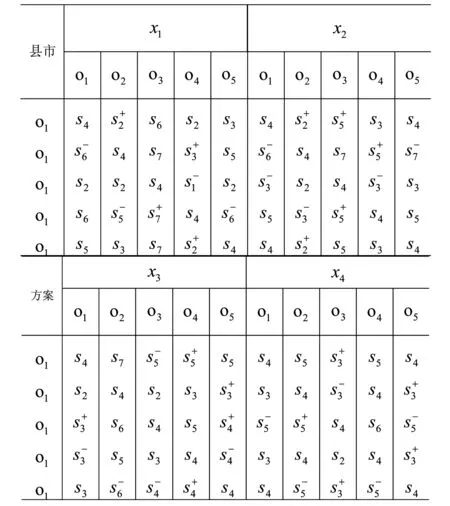
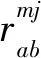
(2)对方案在各指标下的标准量化值(β)进行横向集结得到该专家的总体评价量化值矩阵Q，同理可以得到所有专家的总体评价量化值矩阵Q，即：

(3)根据量化值的排序结果对专家进行分组。得到六个意见组：M1={m10}，M2={m9,m14}，M3={m3,m4,m13}，M4={m2,m7,m16,m17}，M5={m6,m8,m15,m19}，M1={m1,m5,m11,m12,m18,m20}。

(4)计算各组的组内信息一致度。可得：σ1=1，σ2=1.132，σ3=1.057，σ4=1.063，σ5=1.057，σ6=1.146。

(5)计算各组的群体密度权重。根据式(9)求群体密度权重可得：φ=[0.045,0.095,0.156,0.195,0.194,0.315]。

(6)根据式(10)对群体信息进行纵向集结得到最终结果为：ξ=[16.76,17.18,15.02,17.3,16.72]T。

由最终的评价结果可得，鄱阳湖区五个县(区)社会治安服务的最终综合排序结果为o4o2o1o5o3。可见社会治安服务评价效果最好的县(区)是第四个县。

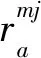
然后，将20位专家对5个县(区)的总体评价量化值取算术平均值(其一致性比率C.R.=0.0235<0.1)，可得：ξ=[4.039,4.137,3.646,4.156,4.041]T。从而有最终的排序结果为x4x2x5x1x3。

通过对比可知，两种方法得到的最优方案一致，不同点在于x1和x5的评价值。传统的二元语义结合层次分析法求得的结果是x1优于x5，而通过本文方法得到的结果是x1优于x5。从所有专家的总体评价量化值矩阵Q数据可以看出，所有专家对x1的评价值较为一致，说明对于x1专家意见较为统一。而所有专家对于x5的评价值较为离散，说明对于x5专家意见存在一定的分歧。在现实情况下，专家意见越一致，意见的可信度就越高。所以虽然对于x5所有专家的算术平均评价值高于x1的，但通过本文的方法可以知道x1和x5的最终评价值是十分接近的，且x1反而略优于x5。相比之下，本文的方法更为合理可靠。

六、结语

本文提出的基于语言评价标准的群体评价方法具有如下几个特点：

(1)针对语言类评价信息的大群体评价问题，将专家对被评价对象进行评价分级的标准进行统一，制定出统一的评价标准体系，同时考虑到评价分级中存在的模糊情况，给出了模糊情况下的二元语义评价分级函数，新函数和评价标准体系能够帮助专家更快速准确地给出评价信息，极大地减少不确定性。

(2)针对语言类评价信息的集结方法进行了探讨，为了提高评价的准确度，本文让专家在同一指标下对被评价对象两两比较，更为细致，得到同一指标下的评价矩阵，再利用矩阵的特征向量和特征根求出被评价对象之间的大小关系，达到量化语言类评价信息的目的。相较于一般的方法，利用该方法得到的结果更加精准。

(3)在解决大群体评价问题时，充分考虑到了群体信息密度分布不均匀的问题，提出根据排序结果一致进行群体分组的方法，定义组内的信息一致度来确定组内评价信息的分散程度，根据信息一致度来确定群体密度权重，从而将群体的评价信息进行集结。该方法综合考虑了评价者和评价指标，信息更加全面准确，更容易得出专家都认同的结果。

(4)在处理语言类评价信息的大群体评价问题时，通过控制专家和指标，让被评价对象之间两两比较得到三维数据。本文先从指标维度进行横向集结，再从专家维度进行纵向集结，这样做不仅可以得到更准确的数据，而且将复杂的评价数据分维进行处理集结，使操作更加简单，减少工作量，具有较高的实用性。