基于PCA_LDA和协同表示分类的人脸识别算法

聂栋栋，贺悦悦，马勤勇

(1.燕山大学 理学院，河北 秦皇岛 066004；2.燕山大学 信息科学与工程学院，河北 秦皇岛 066004)

0 引言

人脸识别是生物识别的一个重要课题，它在身份认证、商业交易、安全保障等多个领域广泛应用。用计算机对人脸进行识别的过程，大致可分为图像获取、特征提取、分类器选择三大步骤。图像获取阶段主要是收集图像数据，通常可以利用一些规范的人脸数据库。特征提取阶段常用的算法有几何特征的方法[1]，弹性图匹配模型[2]，子空间算法，如主成分分析(Principal Components Analysis,PCA)、线性鉴别分析(Linear Discriminate Analysis,LDA)、独立主元分析[3]、小波变换[4]等。在分类阶段，常用的分类器有卷积神经网络[5]、支持向量机[6]、最近邻分类[7]、基于稀疏表示的分类(Sparse Representation-based Classification,SRC)[8]算法等。

本文提出一种基于PCA主成分分析和LDA线性判别分析，通过协同表示分类(Collaborative Representation-based Classification,CRC)进行人脸识别的算法。首先采用PCA和LDA相结合的方法对人脸数据库中的样本信息进行降维和特征提取，然后采用CRC协同表示方法进行分类。该算法克服了主成分分析忽略了数据的类别信息及线性判别分析类内散度矩阵奇异的缺陷，在图像维数较小的情况下就能够取得良好的识别效果，而且算法采用协同表示分类，使它具有比经典的基于稀疏表示的分类算法具有更快的处理速度和更好的抗干扰性能。实验结果也证实，本文算法能够在不同的姿态、光照和面部表情的变化下，尤其是在强烈的高斯噪声干扰下达到更好的人脸识别效果，具有非常好的实用价值。

1 PCA_LDA_CRC算法

本文提出的人脸识别算法，在特征提取并降维阶段采用PCA和LDA结合的方法，在分类阶段采用了CRC协同表示分类方法，因此为了描述方便简称其为PCA_LDA_CRC算法。

1.1 PCA_LDA特征提取方法1.1.1 PCA主成分分析法

主成分分析法是模式识别中常用的一种基于统计的特征提取方法，它通过仅损失一些次要信息达到用更低维的特征向量来表示原本的高维信息的目的。

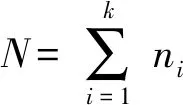
(1)

(2)

在人脸识别中,m被称做平均脸。通过求解协方差矩阵St的特征值和特征向量，可得到一组由特征向量组成的正交基，称为特征脸。样本中任意的人脸图像都可以用这一组基向量线性表示。将协方差矩阵的特征值从大到小排列：λ1≥λ2≥…≥λd≥λd+1≥…，选取前d个特征值对应的特征向量，构成维数为p×d的主成分变换矩阵P。若前d个主成分的累计贡献率较高 (80%～99%)时，就可以在不会损失原图像中太多的特征信息的同时减小人脸特征向量维数。任何一幅人脸图像向变换矩阵P作投影：y=PTaij，即可获得d×1的低维向量y，其中系数表示的是图像在主成分子空间的位置。

PCA人脸识别方法是统计最优的，它使得原图像与投影图像之间的均方误差最小。但是PCA方法同时也存在缺陷。首先它基于图像像素值的统计，外在因素带来的图像差异和人脸本身带来的差异是无法区分的。因此外界因素，如光照变化、遮挡、噪声等都会导致识别率降低。而且由于PCA算法侧重于准确保留原始图像特征，而没有有效利用不同类别之间的差异信息，所以用PCA算法得到的特征是最有表现力的特征，但并不是最有辨别力的特征。

1.1.2LDA线性判别分析

线性判别分析的核心思想是通过求解Fisher判别函数的极值，求得最佳投影向量，将高维空间内的信息投影到更具有分辨能力的低维特征子空间上，并使低维信息达到最小的类内散度和最大的类间散度，即在这个子空间中，各类样本有最佳的可分离性。

令mi为样本集中各类样本的均值：

(3)

则人脸样本图像样本集A的类内散度矩阵Sw和类间散度矩阵SB为

(4)

当类内散度矩阵Sw非奇异时，要想达到最小的类内散度和最大的类间散度，可以求解使类间散度与类内散度比值最大的投影矩阵，即通过如下优化问题求解最佳的投影矩阵L：

(5)

1.1.3PCA_LDA特征提取方法

为了解决上述问题，本文先用PCA对数据进行降维，再用LDA对降维后的数据提取特征，进行二次降维。这样，不仅充分考虑到数据的类别信息，而且克服了LDA对数据要求严格的缺陷。

PCA_LDA特征提取的计算过程如下：

Step 1：由式(1)、(3)分别计算每类样本和所有样本的平均值mi,m；

Step 2：根据式(2)计算协方差矩阵St的特征值及特征向量。选择前d个较大的特征值对应的特征向量，归一化后组成PCA投影矩阵P；

Step 3：根据式(4)计算样本集的类内散度矩阵Sw和类间散度矩阵SB；

Step 4：将Sw和SB投影到矩阵P上，并根据目标函数式(5)计算LDA投影矩阵L；

Step 5：计算PCA_LDA特征提取的总投影矩阵W=P×L.

1.2 CRC协同表示分类

自压缩感知[9]被提出后，就引起了广泛关注，并成功应用于图像处理、模式识别[10]等各方面，如Wright等人[8]利用l1范数最小化求出最稀疏的解进行人脸识别。但是l1范数最小化计算复杂，而且目前人们也就SRC方法成功应用于人脸识别是否就是l1范数的稀疏特性所决定的问题，也一直存在着诸多疑问[11-12]。针对以上问题，本文采用一种l2范数最小化的方法，即协同表示方法进行分类。 协同表示的本质就是利用所有类别中的训练样本来共同表示待识别样本。与稀疏表示的算法相比，协同表示的方法大大减小了计算的复杂度，同时增强的算法抗干扰的能力。

在人脸数据库A的每个类中选取训练样本和测试样本，假设第i类中选取r个作为训练样本，剩余的ni-r个做为测试样本。计算每个训练样本aij在PCA_LDA特征提取总投影矩阵W上的投影：

Dij=WT(aij-m),

(6)

将Dij按列组成字典矩阵D，则D∈Rt×q，其中q=k×r表示训练样本数目,t表示PCA_LDA提取的特征维数，t≤k-1。

假设任何一个测试样本y都可以用字典D中的训练样本线性表示，即y=Dα，其中α=(a1,a2,…,aq)表示系数向量。协同表示方法是通过l2范数最小化求得系数α：

α=arg min‖α‖2s.t. ‖y-Da‖2<ε，

(7)

引入拉格朗日常数λ，则上式可化为

故α=(DTD+λI)-1DTy。

记VT=(DTD+λI)-1DT，则V表示从测试样本向量y到表示系数向量α的投影矩阵。而且矩阵V是独立于测试样本y的，因此当字典D确定后，可以先计算出矩阵VT，然后对每个测试图像y，只需计算α=VTy即可。

最后，测试样本y所在的类为

(8)

1.3 PCA_LDA_CRC算法过程

假设输入样本集A，类别数k，测试样本y，则利用本文算法对测试样本进行分类的具体过程如下：

1) 计算PCA_LDA投影矩阵W；

2) 根据式(6)计算训练样本y在W上的投影；

3) 计算矩阵VT=(DTD+λI)-1DT；

4) 计算系数向量α=VTy；

5) 根据式(8)得出y的分类f(y)。

1.4 算法的计算复杂度分析

在PCA分析阶段，最耗时的处理是对大小为p×p的协方差矩阵St求d个最大的特征值，其复杂度为O(p2d)；在LDA分析阶段，将SB和Sw投影到大小为p×d投影矩阵P上后，大小都为d×d，该阶段最耗时的处理是求逆矩阵和求特征值，其复杂度是O(d3)；在CRC分类阶段，最耗时的是求(DTD+λI)-1，因此该阶段的复杂度是O(q3)。上述过程对所有测试样本只需要计算一次，因此假设总测试样本数目为s，则复杂度为O((p2d+d3+q3)/s)。又因为p≫d，p≫q且d,q,s量级相当，故本文算法的复杂度可简化表示为O(p2)。

2 实验结果

为验证算法的有效性，实验分别在ORL库[13]和YALE库、部分FERET库上进行，其中ORL人脸库包括40个人的400张图片；YALE库包含15个人的165张人脸图片，每个人11张不同表情与光照条件；FERET库包含1 400张图，每人7张，本文选择其中的40个人作为代表，分别进行实验。这些实验数据库的人脸图像在光照条件、面部表情等方面存在较大差别，因此这些数据库不仅可以验证算法的有效性，而且可以验证算法的鲁棒性。

首先，实验对本文算法PCA_LDA_CRC与其它几种典型相关算法的识别率进行了比较，结果见表1～3。其中PCA_LDA_SRC与PCA_LDA神经网络与本文PCA_LDA_CRC采用相同的特征提取算法，但在分类时分别采用SRC、神经网络、CRC进行分类。而2DPCA_CRC算法则采用与本文算法不同的2DPCA降维，相同的CRC分类。CRC算法则直接采用下采样降维后进行CRC分类。表中r表示从每类人脸图像中随机抽取的作为训练样本的个数。由于样本抽取的随机性，所以表中结果是10次测试的平均值。实验中所有CRC算法中的拉格朗日参数λ为取经验值0.2。这是根据对参数在0.1到1之间，每隔0.1进行一次实验，最终各个人脸数据库下的综合表现取最好的。

表1 ORL人脸库上的实验结果
Tab.1 Test results on ORL face database%

算法样本维数r=2r=3r=4PCA_LDA_CRC3981.13 90.07 92.08PCA_LDA_SRC3980.0488.1189.58PCA_LDA神经网络3941.5657.8663.33CRC5667.0672.29 77.42 2DPCA_CRC1 68078.7587.29 89.08

表2 YALE人脸库上的实验结果
Tab.2 Test results on YALE face database%

算法样本维数r=2r=3r=4PCA_LDA_CRC1492.1492.9394.92PCA_LDA_SRC1486.6787.4389.11PCA_LDA神经网络1478.8180.4483.11CRC10080.50 82.38 87.89 2DPCA_CRC40084.00 86.67 87.78

表3 FERET人脸库上的实验结果
Tab.3 Test results on FERET face database%

算法样本维数r=2r=3r=4PCA_LDA_CRC3970.0076.6786.25PCA_LDA_SRC3965.6375.8383.75PCA_LDA神经网络3940.0043.7550.00CRC40043.0049.1765.002DPCA_CRC1 20019.3826.6738.75

从表1～3结果可以得出以下结论：

1) 本文提出的PCA_LDA_CRC在使用较少的样本维数的条件下，获得了比其它几种相关算法更好识别率。

2) 在ORL、YALE和FERET人脸库上，本文PCA_LDA_CRC算法的识别效果较为稳定。而CRC和2DPCA_CRC在FERET人脸库的识别效果都明显比其它两种数据库上的识别效果差很多。PCA_LDA_神经网络只在YALE人脸库上稍好，在其它两个数据库上识别效果都较差。这证实本文算法能够更好地消除光照、面部表情等方面的影响，算法具有良好的稳定性。

其次，为了定量分析算法的时间复杂性，本文对上述各算法的处理时间进行了统计。以ORL人脸数据库为例，每类人脸图像的训练样本数分别是r=2、3、4、5时，平均完成1幅人脸图像识别的时间，见表4所示。算法采用MATLAB 7.0编写，表中统计的处理时间是在台式PC(Intel Core i5-2320 CPU@3.00 GHz，16 GB内存)上运行10次后的平均值。

表4 ORL人脸库上的处理时间
Tab.4 Processing times on ORL face databasems

算法r=2r=3r=4r=5PCA_LDA_CRC5.50 6.36 7.22 7.49 PCA_LDA_SRC114.86 102.13 92.41 81.76 PCA_LDA神经网络7.48 8.34 9.70 10.60 CRC1.50 1.561.58 1.57 2DPCA_CRC1.661.711.811.94

从表4中可以看出，本文算法的时间复杂度远低于采用稀疏分类的PCA_LDA_SRC，略低于采用神经网络分类的PCA_LDA_神经网络，略高于2DPCA_CRC和CRC算法。但结合表1中的识别率可知，本文算法在略增加运行时间的同时大大提高了算法识别率，并增强算法稳定性，因此具有良好的应用价值。

再次，实验还比较本文算法与其它类型的人脸识别算法[14]的识别率，见表5所示。

从表5中可以看出，除了在ORL数据库中每类训练样本数r=7时，文献[14]的DH-NMF算法的识别率略高于本文算法，其它情况下均是本文算法的识别率更高，尤其是在YALE数据库下的两种算法识别率的差别很大。这也证实本文算法受人脸图像在光照、面部表情等方面的差异的影响较小，算法具有更好的稳定性。

表5 与文献[14]算法的识别率比较
Tab.5 Comparison with the method of the literature[14]

r=3r=5r=7ORL数据库PCA_LDA_CRC90.0793.6595DH_NMF82.991.295.4YALE数据库PCA_LDA_CRC92.1494.9295.71DH_NMF75.078.383.3

最后，为了验证算法在噪声干扰下的鲁棒性，实验还测试了在样本图像中加入高斯白噪声后算法的识别能力。图1给出了ORL库中的一个原始样本图像以及加入均值为0，方差分别为0.05、0.01、0.15、0.20、0.25的高斯白噪声后的图像。

图1 原始人脸图像和不同方差下的噪声图像
Fig.1 Original face image and noise images with different variance

表6比较了加入高斯白噪声后，本文及其它几种相关算法的人脸识别率。 用于实验的样本维数与表1相同。所有实验结果均为测试10次的平均数。

表6 ORL人脸库上的实验结果
Tab.6 Test results on ORL face database%

高斯噪声方差0.050.100.150.200.25PCA_LDA_CRC79.6470.1965.3656.0750.47PCA_LDA_SRC77.8666.0764.6450.3645.71PCA_LDA神经网络49.2934.6431.7928.5718.21CRC37.1427.521.0716.0712.142DPCA_CRC63.5753.9350.7146.4339.29

从表6中可以看出：当噪声逐渐加强时，几种算法的识别率都有所下降，但在同样等级的噪声干扰下，本文算法的识别率比其它几种算法的识别率更高，抗噪能力更强。而PCA_LDA_SRC 和2DPCA_CRC算法在噪声干扰下的表现一般，PCA_LDA神经网络和CRC算法的抗噪能力则较差。

3 结论

本文提出了一种基于PCA_LDA降维和CRC协同表示分类的人脸识别算法。该方法融合了PCA算法、LDA算法和CRC算法的特点， 它能够在有效提取样本特征的同时，更准确的进行人脸分类。实验证明，本文算法在三种常用的人脸数据库上的测试结果稳定，能够更好地消除光照条件、面部表情等方面的影响；相比其它几种算法，本文所提算法在样本维数较低，训练样本较少时，能够在整体上获得了更好的识别效果，而且该算法在外界噪声干扰的情况下，识别率也一直较高，算法的抗噪性能较强。因此，本文算法具有良好的实用价值。