分数阶混沌系统的模糊保性能同步控制
(郑州航空工业管理学院 数学学院,河南 郑州 450015)
混沌系统的同步已经成为研究的热点问题[1,2],例如:文献[3]研究了多涡卷混沌系统的有限时间滑模同步,给出了非线性超曲面的构造和设计.文献[4]研究分数阶Victor-Carmen系统的同步,文献[5]研究了分数阶不确定多混沌系统的终端滑模同步,文献[6] 研究了Genesio-Tesi混沌系统的适应转移函数滑模同步.文献[7] 用两种方法研究了分数阶Newton-Leipnik系统的自适应滑模同步.另一方面,模糊系统的同步引起了控制界的高度关注,文献[8] 研究了分数阶模糊混沌系统的预测投影同步.文献[9]研究分数阶统一模糊混沌系统的非脆弱控制.文献[10]研究了分数阶神经网络模糊系统的同步,在以上研究的基础上,研究分数阶混沌系统的模糊保性能同步,能够使系统误差收敛到原点.得到主从系统模糊保性能同步的充分条件.
1 主要结果
定义[11]Caputo分数阶导数定义为
以分数阶混沌系统为主系统
(1)
设计从系统为
(2)
其中[ΔA,ΔB]=DF(t)[E1,E2],FT(t)F(t)u(t)≤I,定义e(t)=y(t)-x(t)得误差系统方程
(3)

(1)式可被T-S模糊模型描述为:
ifz1(t) isMi1and…andzr(t) isMirthen
(4)
其中,Mi j(j-1,2,…,r)是模糊集合,r是模糊规则数,x(t)∈Rn是系统状态,Ai∈Rn×n,z1(t),…,zr(t)是模糊前件变量,模糊模型可表示为
(5)
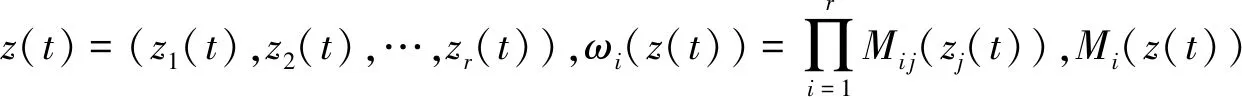
(6)
以(6)作主系统的模糊模型,从系统可表示为
(7)
定义e(t)=y(t)-x(t),可得误差方程模糊表示
(8)
引理1[12]给定适当维数的矩阵Y,D和E,F,则Y+DFE+ETFTDT<0对所有满足FFT≤I的矩阵F成立,当且仅当存在一个常数λ>0,使得Y+λDDT+λ-1ETE<0.
引理2[13](Schur补引理)设A,B,C为适当维数的矩阵,则下面三个式子等价:
(1)A<0,C-BTA-1B<0;
(2)C<0,A-BTC-1B<0;
定理1 如存在对称正定的矩阵P以及矩阵K,若满足矩阵不等式
Q+KTRK+P[Ai+BiK+DF(Ei1+Ei2K)]+[Ai+BiK+DF(Ei1+Ei2K)]TP<0,
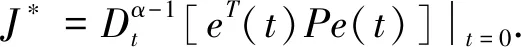
证明构造Lyapunov函数V(t)=eT(t)Pe(t),沿系统(8)求分数阶导得到
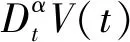

定理2 若存在对称正定的矩阵P以及矩阵K,若满足矩阵不等式
(9)
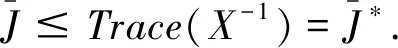
证明若定义Y=Q+KTRK+P(A+BK)+(A+BK)TP则(9)可表示为
Y+PDF(Ei1+Ei2K)+(Ei1+Ei2K)TFT(PD)T<0,
由引理1,得到Y+εPDDTP+ε-1(Ei1+Ei2K)T(Ei1+Ei2K)<0.
由引理2,上式等价于
对上式分别左乘和右乘diag{P-1,I,I,I},若记X=P-1,W=KP-1.所以得到(9).
2 数值仿真
保性能控制律u(t)=[-0.430 2,1.798 9]e(t),性能上界J*=10.689 2.系统的误差如附图.
附图 系统误差
3 结 论
研究了分数阶混沌系统的模糊保性能同步,根据分数阶混沌系统同步控制理论获得主从系统取得模糊同步的充分条件,结论表明分数阶混沌系统的驱动响应能够取得模糊保性能同步.研究分数阶混沌系统的有限时间同步是下一步需要研究的问题.

