对流传热问题的粒子-网格混合方法数值模拟
李勇霖,陈荣华,田文喜,秋穗正,苏光辉
(1.西安交通大学 动力工程多相流国家重点实验室,陕西 西安 710049;2.西安交通大学 核科学与技术学院,陕西 西安 710049)
20世纪后期,随着计算机运算能力的提高,数值模拟技术得到了飞速发展。数值模拟技术从对物理问题的数学描写出发,使用各种数值方法求得物理问题的数值解,分析数值解进而探求物理问题的本质规律。数值模拟的实现关键在于有效算法的开发,在计算流体力学(CFD)领域尤为如此。现有传统的数值方法如有限差分法(FDM)、有限元法(FEM)及有限体积法(FVM)等都是在对求解区域划分网格后进行数值求解。传统的数值算法虽已日趋成熟,但在处理复杂几何形状、高速撞击、流固耦合及自由面追踪等特殊问题时,还面临着网格扭曲等挑战性问题[1]。
相比于网格法,使用移动粒子方法来进行数值模拟可对上述问题进行很好的分析。尤其是流体的拓扑变形不能通过移动及固定网格进行分析,却能通过移动粒子方法进行分析。移动粒子方法的另一个优点是,在计算对流时,直接通过粒子的运动计算而不需考虑数值扩散问题[2]。因为这些优势,近几十年来涌现出了粒子数值分析方法。这些粒子数值分析方法大致能分成两种类型:第1类是建立在概率论模型上,如分子动力学方法[3]、蒙特卡罗方法[4]等;第2类是建立在确定论模型上,如光滑粒子动力学(SPH)方法[5]和移动粒子半隐式(MPS)方法[2]等。第1类方法需对大量粒子的行为进行长时间跟踪,直到获得一精确的平均值,相对而言,第2类方法不需如此大的内存和计算机时间。
在此之后,一些粒子法与网格法耦合的方法被提出,如MPS-MAFL[6]及有限体积粒子(FVP)[7]方法。MPS-MAFL方法的液相通过粒子离散,气相不需要离散而只是为液相提供压力边界条件,气相的压力通过气体状态方程确定;FVP方法中,气相使用欧拉网格表示,液相通过拉格朗日粒子进行离散。FVP方法实际是将MPS方法计算中的粒子定义为1个正方体,其体积即为原粒子直径的立方。在实际计算中,如果按固定的有限体积进行划分,当粒子发生移动后,粒子排布不再如初始状态那般规则,有限体积在计算域内会出现重叠,而且在相邻有限体积粒子中间会出现间隙。
由于拉格朗日粒子法的本质,MPS方法中的固壁边界条件很难像网格法一样严格实施,这是因为当计算的粒子位于计算域内部时,粒子的支持域没有被边界截断,计算结果能达到较高精度,当粒子位于边界附近时,支持域会被边界截断,此时,普通的核近似方法在边界的计算上不再适用。这个问题是限制粒子法发展的关键性问题。对于此类问题,在SPH方法的改进上已做了较多尝试[8-15],包括边界施加方法和虚粒子法。边界施加方法是对边界的粒子施加一个额外的作用力,实现起来较为简单,但物理意义不明确且数值稳定性较差;虚粒子法则在边界外侧额外布置一些粒子以修复边界附近粒子缺失现象,此法理论依据较完善、精度较高,但对于复杂形状边界的处理比较困难。在计算存在自由表面的流体流动问题时,常通过某种条件确定自由表面粒子,并认为自由表面粒子的压力为0,通过此处理,能使MPS方法在计算自由表面流动问题中获得较精确的解。
在计算流体力学领域,传热问题的研究是普遍存在的,当使用MPS等粒子方法进行传热计算时,也会出现计算精度的问题。对于传热问题而言,如果计算边界不是恒温,那么将粒子近似法直接应用于求解传热问题是不正确的,即粒子模型的流动边界处理方式不能直接应用于传热问题的计算,即便是FVP方法在求解传热问题时得到的结果也不尽人意。
为克服MPS方法存在的不足,本文在MPS方法的基础上,提出一种粒子-网格混合求解方法,即使用MPS-FVM耦合的方法对对流传热问题进行求解,既能保留粒子法在处理复杂几何形状、高速撞击、流固耦合和自由面追踪问题的优势,又能在处理传热问题时,消除求解域边界的计算误差以及整体计算获得精确的数值解。
1 数学物理模型
1.1 控制方程
粒子-网格混合方法中的连续性方程、动量守恒方程和能量守恒方程分别为:
(1)
(2)
Ein+Eg=Est
(3)
其中:ρ为密度;u为速度;p为压力;ν为运动黏性系数;f为外力;t为时间;Ein为单位时间控制体积内能量净入量;Eg为单位时间控制体积内能量产生量;Est为控制体及内能量变化率。
在粒子-网格混合方法中,MPS方法用于求解动量守恒方程,FVM用于求解能量守恒方程,则前两个方程以微分形式给出,能量方程以积分形式给出。
1.2 粒子相互作用模型
在MPS方法中,粒子之间的相互作用通过核函数实现,每个粒子仅与其作用半径内的有限个粒子发生相互作用。本文算例中使用的核函数为:
w(|rj-ri|)=
(4)
其中:ri、rj分别为i粒子和j粒子的坐标;re为粒子作用半径。
i粒子的粒子数密度ni定义为:
(5)
对于不可压缩流体,流体密度保持定常。由于流体密度与粒子数密度呈正比,其粒子数密度维持为1个常数。
某物理量在i粒子处的梯度矢量可通过梯度模型求解,梯度模型在MPS方法中被用来求解压力的梯度项。在动量守恒方程中,扩散项以Laplace算子表示,使用Laplace模型求解。梯度模型和Laplace模型分别为:
(6)
(7)
其中:φ表示物理量;d为计算的空间维度;n0为初始粒子数密度;λ为邻居粒子和中心粒子间距的方差,它的出现是为了考虑粒子扩散范围的时间效应。
1.3 能量守恒方程的求解
在对粒子运动进行求解后,将获得每个粒子的坐标位置,然后根据粒子坐标,对计算域进行网格划分,每个粒子中心将对周围有1个控制体积。而这个控制体积是根据该时刻的粒子间位置决定的。实际上,在计算中,求解获得粒子在该时层的坐标后,可对i粒子的邻居粒子进行分析,每个邻居粒子对i粒子有1个作用面积,在二维计算中,作用面积Aj定义为:
Aj=ljl0
(8)
其中:lj为j粒子与i粒子连线的垂直面作用线;l0为初始粒子间距。
那么对于i粒子的控制体积则为:
(9)
对于无内热源的导热问题,式(3)的能量方程可写成:
(10)
其中:κ为导热系数;Ti和Tj分别为i、j粒子温度;cp为比定压热容;上标n表示时层。
1.4 算法流程
粒子-网格混合方法求解对流传热问题的算法流程如图1所示,在求解实际问题时,先根据具体问题设定粒子初始布置,然后使用MPS方法求解流动问题,求解得到粒子坐标位置后对其进行网格划分,再使用FVM对传热进行求解。
2 导热问题的验证
图2示出一维半无限平板导热问题算例模型,其计算域尺寸为41×20,左端红色粒子设定为恒温,即Tl=1 K,右边绿色粒子初始温度为0 K,且温度可变。图2b是按照粒子位置划分的FVM网格,可看出,在平板线边缘,网格的体积为原始体积的一半;而在平板角边缘,网格的体积则为原体积的1/4。平板的物性分别取为密度ρ=1 000 kg/m3、比热容c=1 J/(kg·K)、导热系数κ=1 W/(m·K)。

图1 粒子-网格混合方法的流程Fig.1 Flow chart of particle-grid hybrid method
算例的初始条件如下。t=0 s:T=Tl=1 K,x=0;T=0 K,0 在这个算例中,使用MPS方法及粒子-网格混合方法分析了不同时刻平板温度的分布,结果如图3所示,并将计算结果与精确解进行了比较,结果如图4所示。可发现,在导热前期,使用MPS方法求得的结果与解析解之间有较大差距,特别是在靠近热源(即恒温)处的粒子,温度误差相当大,但随时间的变化,这个误差逐渐减小。使用粒子-网格混合方法进行计算时,前期误差虽然存在,但误差较小,且随时间的变化,误差逐渐展平至可忽略不计。图5示出距离恒温源最近(x=0.025)的一列粒子的纵向温度分布。实际计算中,一维半无限大平板的上、下端处设置为绝热,等温线应呈直线分布,使用MPS方法计算时出现了等温线弯曲现象,这是由于粒子相互作用模型,即Laplace模型不适合求解温度Laplace算子。使用粒子-网格混合方法计算的结果,前期虽存在误差,但误差很小,且误差随时间的变化而逐渐变得更小,后期误差几乎可忽略不计,且在计算时间范围内,等温线一直呈直线分布,符合理论分析的结果。 a——MPS粒子布置;b——FVM网格划分图2 半无限平板导热算例Fig.2 Example of semi-infinite plate thermal conductivity a——前期;b——后期图3 半无限平板温度分布Fig.3 Temperature distribution in semi-infinite plate a——前期;b——后期图4 数值计算温度与精确解间的误差Fig.4 Error between numerical temperature and exact solution a——前期;b——后期图5 x=0.025处的温度分布Fig.5 Temperature distribution at x=0.025 不同温度的两个垂直侧边方腔内的自然对流是用来测试不同程序计算传热问题有效性的典型算例。本文选取了方腔自然对流的标准题[16]进行计算,所述问题如图6所示,方腔左侧壁面为高温恒定温度Tl=1 K,右侧壁面为低温恒定温度Tr=0 K,上、下壁面绝热。腔体为正方形,边长为L,流体Pr为0.701,四周为固体壁面,取无滑移条件,流体符合Boussinesq假设。 本文方腔内自然对流的初始条件如下。t=0 s:u=v=0,T=Tl=1 K,x=0;u=v=0,T=Tr=0 K,0 图6 物理模型Fig.6 Physical model 在模拟计算方腔自然对流时,设定了如图6的初始条件及边界条件,随计算的进行,逐渐达到稳态过程。图7示出瑞利数Ra=106的瞬态及稳态结果。 a~d——瞬态;e——稳态图7 Ra=106的瞬态及稳态结果Fig.7 Transient and steady-state results with Ra=106 a——温度等温线图;b——流线图图9 Ra=105的计算结果Fig.9 Calculation result of Ra=105 本文还计算了Ra分别为103及105时方腔自然对流的结果,如图8、9所示,当Ra较小时,方腔内部的等温线几乎沿竖直方向,流动的典型特性是在方腔中间出现了1个大涡。当Ra增大时,方腔内部等温线逐渐变为水平,并且在热冷壁面附近的薄边界层内仍保持垂直,这说明,当Ra较小时,换热主要是热传导为主,随着Ra的增加,换热逐渐变为由对流换热为主导地位。Ra增大后,方腔内部的大涡分裂成两个。将计算所得的平均Nu与基准题解进行对比,结果如图10所示,可发现粒子-网格混合方法在计算方腔内自然对流时具有较高的精度。本文选择了方腔对流达到稳定状态后的平均Nu进行对比。为了对计算所得的平均Nu进行不确定度分析,本文对稳定状态后20个时刻的平均Nu进行分析,可得到Ra为103~106的方腔对流平均Nu的标准偏差uNu为: 图10 平均Nu结果对比 Fig.10 Comparison of average Nu 平均Nu的标准偏差如图11所示。由图11可见,粒子-网格混合方法计算得到的平均Nu的标准偏差在2%以内,说明了粒子-网格混合方法在计算对流换热问题时所得到的结果是比较可靠的。 为研究粒子-网格耦合方法的工程适用性,对不同计算量的方腔对流进行了计算时间对比,因为粒子-网格混合方法已实现OpenMP的单节点多核并行算法计算,图12示出不同计算量的方腔对流问题在使用计算机不同核数的单个时间步长计算耗时,计算机型号为RR CPU E5-2697 v3 2.6 GHz。由图12可见,计算方腔内对流问题时,使用的粒子数量越多,单个时间步长耗时越长,当使用更多的CPU参与计算时,能在一定程度上缩小单个时间步长耗时,总地来说使用并行算法的粒子-网格混合方法在一定程度上提高了计算效率。目前在并行效率上,还没有完成更高并行效率的MPI并行及GPU并行算法的搭建。若完成更高并行效率的算法搭建,基于粒子-网格耦合方法有可能应用于大规模的工程计算。 图11 平均Nu的标准偏差Fig.11 Standard deviation of average Nu 图12 不同粒子数量、CPU数量的单个时间步长耗时 Fig.12 Usage time of single step under different particle numbers and different numbers of CPU 本文针对MPS方法在求解导热问题时存在的边界不精确情况,对MPS方法进行了改进,提出了使用MPS方法求解动量守恒方程、使用FVM求解能量守恒方程的粒子-网格混合方法。该方法使用MPS方法求解流动问题,保留了MPS方法在求解大变形问题及相变问题方面所具有的优势,且还解决了原方法求解导热方程不精确的问题。本文研究的粒子-网格混合方法仅适用于二维情况,对于三维情况还需做进一步研究。




3 方腔内自然对流


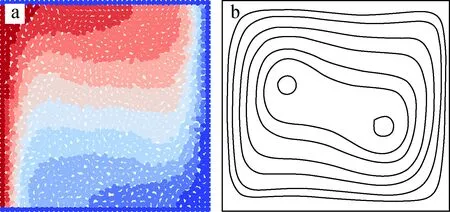

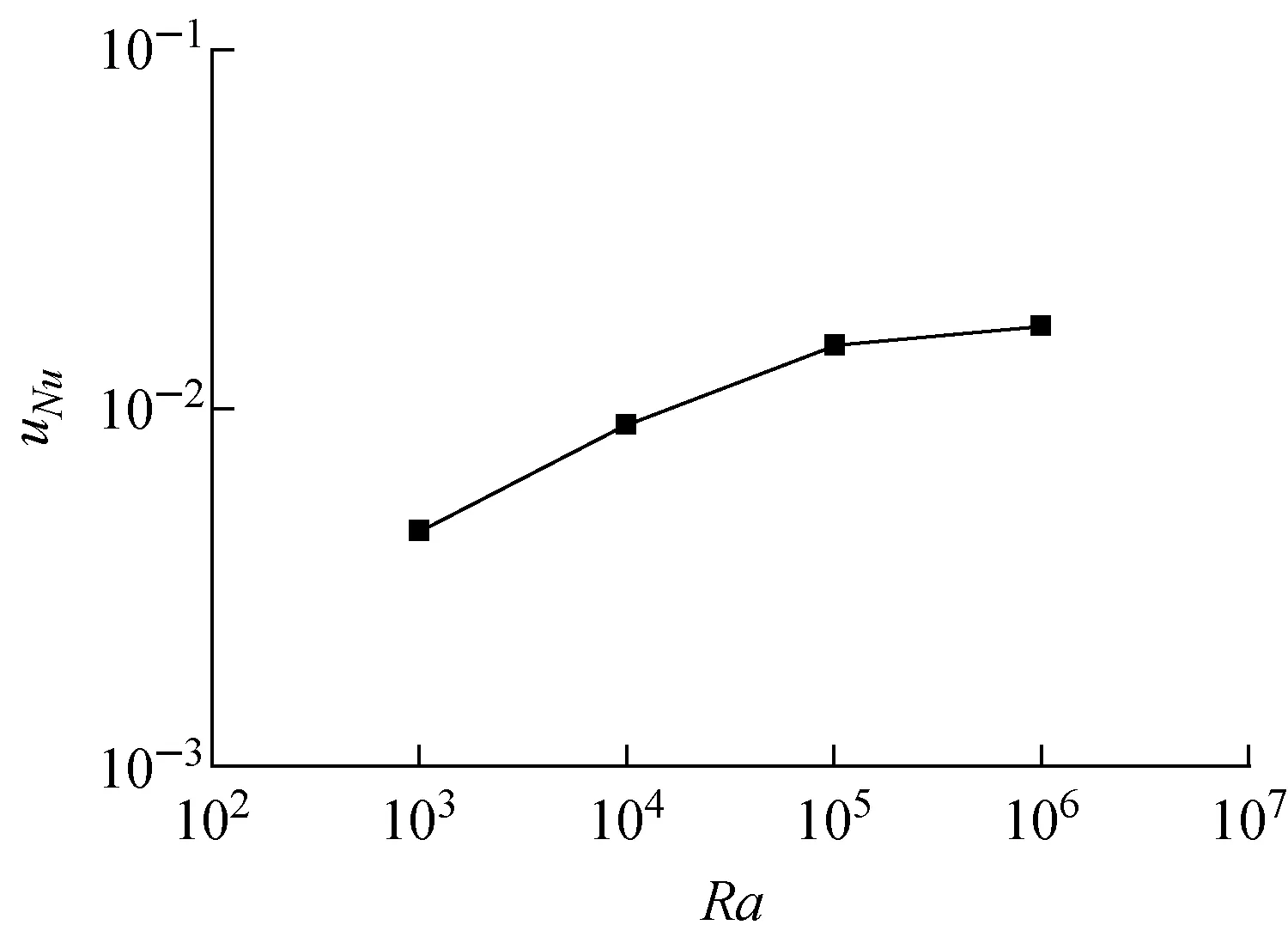

4 结论

