基于映射适应卷积理论的各种映射的抗混叠效果比较
郭学敏
(四川大学计算机学院,成都610065)
0 引言
如今随着人工智能的飞速发展,在三维游戏、真实场景模拟、虚拟现实[1]等应用中,对于图像的质量要求越来越高,很多大型场景的模拟和重建[2]都需要用纹理映射技术[3]合成高质量的图片,而纹理映射技术多种多样,针对不同的维度,不同的过程,不同的几何图形都会有不同的纹理映射技术。纹理图像在映射到实际物体的时候不可避免的会产生混叠,像素缺失等现象,现有的经典抗混叠算法有Williams[4]提出的Mip-Map,运用图像金字塔数据结构进行预过滤处理和后来惠普公司在Mip-Map 的基础上进行改进了,提出了一种新的方法称为Rip-Map,这个方法主要是针对Mip-Map 得不到长方形纹理区域的缺陷进行改进。不同于现有的经典反混叠算法Mip-Map、Rip-Map,本文针对一种新型的卷积理论,探讨它使用在不同纹理技术中的抗混叠效果。
1 映射模型介绍
1.1 正向映射法
正向映射法是二维纹理映射[5]算法中比较常见的一种,将纹理空间的像素映射到图像空间,在这个过程中,会先将纹理空间中的二维纹理映射到实际物体的三维物体表面,用Catmull 算法[6]通过映射函数将二维纹理与物体的曲面坐标匹配,匹配坐标可以确定在三维物体表面的纹理像素坐标位置及大小,再通过线性插值计算三维物体表面对应匹配点的纹理像素中心灰度值,并且将该点的灰度值作为三维物体表面该处的像素中心采样点的纹理属性,然后再映射到二维的图像空间。将纹理空间的像素坐标设为(u,v),图像空间的坐标设为(x,y),那么它们之间的正向映射函数可表示为:
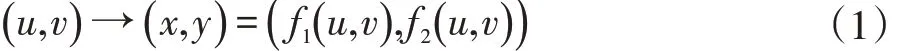

图1 正向映射示意图
正向映射有个非常明显的缺点,就是映射过程当中映射过去的是纹理图像的灰度值,信息较少,纹理空间的像素坐标与物体表面的曲面坐标并不能完全的一一对应,肯定会产生形变,没有匹配到对应的纹理像素的区域会产生空洞,而匹配到不是本区域的纹理像素的区域则会产生多射,这些纹理的缺失和形变都是我们不希望发生的。
1.2 逆向映射法
逆向映射法[7]的映射过程和正向映射法正好相反,它是通过映射函数给物体的曲面坐标在纹理空间寻找对应的纹理像素坐标,找到坐标后,在计算三维物体表面坐标中心的像素值之前,要用重采样方法对纹理图像进行重采样,重采样的过程中可能会产生混叠现象,然后将重采样后计算的像素值映射到纹理空间。逆向映射法算法可如下表示:

1.3 球面映射法
球面映射法[8]对应的物体曲面是球面,将二维空间的纹理坐标映射到球面上,根据球面上的每个点的法向量坐标生成对应的纹理坐标,二维纹理坐标和球面法向量坐标如图2 所示。

图2 纹理坐标与球面坐标表示图
外围的虚线坐标表示二维纹理的坐标,中心的实线坐标表示球面法向量的坐标,从图中可以看出纹理坐标的范围是u ∈( 0,N ),v ∈ ( 0,N ),而球面法向量坐标的范围是x ∈(- N,N ),y ∈ (- N,N )。球面映射法的核心就是要找到这两个区间的映射关系,一般用反正弦函数y=acrsin(x)来实现两者中的对应关系。由于该函数的定义域 x=(-1,1)和值域 y=(-π/2,π/2),我们可以得到映射关系表达式:
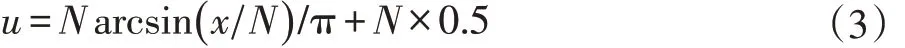

其中u,v 是纹理坐标的横坐标与纵坐标,x,y 是球面的法向量的横坐标与纵坐标,N 表示最后要得到的平面视图N*N 的大小。
1.4 柱面映射法
球面映射法对应的物体曲面是柱面,将二维空间的纹理坐标映射到柱面上,假设是半径为r,高为h 的圆柱,用柱面方程表示如下:

那么我们将纹理空间[0,1]×[0,1]的范围和柱面空间[0,2π]×[0,1]进行线性变换,变换之后的表达式如下:


图3 柱面映射示意图
2 映射适应卷积
2.1 混叠与抗混叠
当对于连续信号做采样处理并将其数字化的时候,如果取样频率低于两倍奈奎斯特频率,那么把取频率还原成连续信号时产生交叠而失真的现象叫做混叠,在图像上又可以叫作叠影。如果混叠发生在时间域上,可以叫时间混叠,发生在频率域上,叫做空间混叠。出现混叠现象的时候,高频信息和低频信息交杂在一起,还原出的原始信息会有很大的缺陷,为了得到更好的原始信息,最好先做抗混叠处理。
采样必然产生混叠,那么比较常见的抗混叠处理方法有两种,一种是缩小采样时间间隔,由于现在的技术有限,许多信号本身可能含有0 ~∞范围内的频率,不可能将采样频率提高到∞,那么这种方法的可适用范围就很有限。另一种是用滤波器,在采样频率一定的前提下,通过低通滤波器[9]过滤掉一些高频成分,通过的信号就不会出现混叠现象。这是一种理想的滤波器,实际中的滤波器很难达到理想的状态。下面我们将介绍一种新的抗混叠方法。
2.2 映射适应卷积理论介绍
卷积其实是让两个函数做积分生成一个新的函数的运算,常见的有高斯卷积,假设f(x),g(x)是R 上的可积函数,积分产生的新函数为h(x),那么卷积的表达式如下:

但是,当其中一个做积分的函数通过映射变为一个新的表达式之后,再做卷积得到的新函数和之前不一样。有人提出了一种新的卷积理论叫做映射适应卷积理论[10]。在该理论中,作者通过数学推导,给出了一个能适应映射后的卷积公式:

其中x′=g(x′′)一个从该模拟图像到原始图像M(x)的映射,并且该映射为微分同胚映射,Jg-1(x)表示映射x′′=g-1(x′)的雅可比行列式的绝对值,κ(x)∈L1(R2)为卷积核函数。该卷积本身是在标准高斯卷积的基础上进行改进的,并且从文献[10]的定理2.3 可知映射适应卷积相比标准高斯卷积具有映射适应性。
2.2 算法介绍
从上面的理论知识我们已经知道,映射适应卷积可以让经过映射后得到的函数 f(h ( x ))和没见过映射后的函数 f( x )在与另一个函数g(x)做积分运算后结果相同,那么该运算表达式还可以是:

其中,k( x,y )=f(h(x,y))是f( x,y )经过映射后的函数,而映射h 的定义为:

Jh( )x,y 是原函数的雅克比,表达式如下:

那么对于逆映射h-1的雅克比行列式如下:

3 反混叠实验结果
3.1 验证该理论具有抗混叠性
通过前面的理论介绍,我们将映射适应卷积加入各种纹理映射方法中,为了验证我们这种方法在各种映射方法中的抗混叠效果,我们将直接映射的结果图和做了抗混叠处理的映射结果图相比较,实验采用的图片是由两个函数生成的:
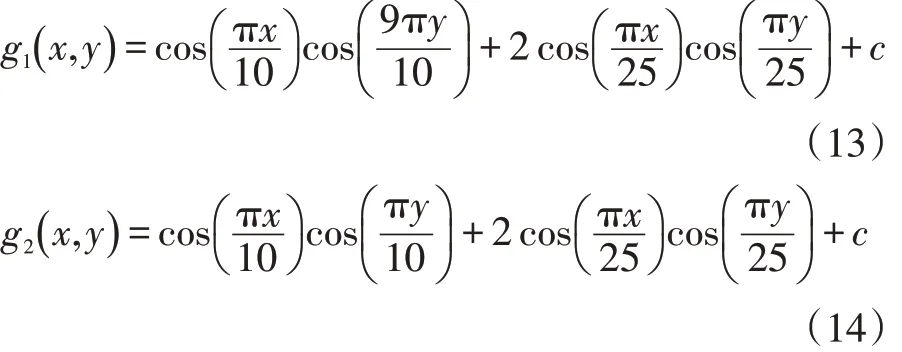
其中c 是常量,当g1(x,y)和g2(x,y)小于0 时,可以调节c 的值,使得g1(x,y)和g2(x,y)的值为0。
3.2 实验结果

表1 各映射的抗混叠结果比较
3.3 正映射结果比较

图4
未做抗混叠处理映射后的图(左)、用MA 卷积做抗混叠处理映射后的图(中),原始图片(右)。左图与原始图的相似度为0.738411,中图与原始图的相似度为0.763275。做抗混叠处理之后,比之前相似度增长0.024864。
3.4 逆映射结果比较

图5
未做抗混叠处理映射后的图(左)、用MA 卷积做抗混叠处理映射后的图(中),原始图片(右)。左图与原始图的相似度为0.775947,中图与原始图的相似度为0.805223。做抗混叠处理之后,比之前相似度增长0.029276。
3.5 球面映射结果比较

图6
未做抗混叠处理映射后的图(左)、用MA 卷积做抗混叠处理映射后的图(中),原始图片(右)。左图与原始图的相似度为0.642653,中图与原始图的相似度为0.697859。做抗混叠处理之后,比之前相似度增长0.055206。

图7
未做抗混叠处理映射后的图(左)、用MA 卷积做抗混叠处理映射后的图(中),原始图片(右)。左图与原始图的相似度为0.505829,中图与原始图的相似度为0.586922。做抗混叠处理之后,比之前相似度增长0.081093。
由实验图片可以看出左图都产生了混叠现象,而通过映射适应卷积理论的抗混叠算法生成图像没有产生混叠现象,因此该映射适应卷积理论抗混叠算法中从球面到平面的纹理映射反混叠有很好的抗混叠效果。
4 结语
本文主要研究映射适应卷积理论在不同纹理映射方法中的抗混叠效果,在论文当中,我们首先介绍了几种常见的纹理映射方法,如正向映射法、反向映射法、球面映射法和柱面映射法,然后详细讲解了映射适应卷积的理论,以及如何将卷积和映射结合起来。从实验结果我们可以看出,映射适应卷积在柱面映射法中的抗混叠效果最明显,在正向映射法相似度的增长幅度最低,本次实验只验证了常见的几种纹理映射法,在后续的研究中可以加入新的对比实验,例如比较经典抗混叠方法Mip-Map、Rip-Map 在这些纹理映射法中的效果和映射适应卷积的抗混叠效果哪个更好。

