基于MWC 多测量向量的高效恢复算法
朱嘉微,符博娟,李健
(四川大学电子信息学院,成都 610065)
0 引言
随着无线通信的快速发展,通信频点越来越高,传统的信号采样率由于受限于Nyquist 采样定理已成为制约信号处理发展的一个瓶颈。压缩感知(Compressed Sensing,CS)理论的出现打破了Nyquist 采样率的瓶颈,可以利用低于Nyquist 采样率的速率对数字信号进行采样还原,而调制宽带转换器(Modulated Wideband Converter,MWC)真正意义上实现了模拟信号的欠Nyquist 采样及还原,在分布式电磁频谱感知领域有很广阔的应用前景[1-3]。准确性和实时性是频谱感知技术中的关键,下面针对这个问题进行深入研究并提出改进方法。
基于MWC 的频谱感知主要分为三个阶段:一是宽带稀疏信号的采样,二是采样信号的降维处理,三是利用采样数据进行信号恢复,其中降维处理过程是恢复过程的关键,既要求降低采样数据的维度,又要保持信号的原始信息不被丢失。目前已有关于MWC 采样数据降维处理技术,在文献[4]中就提出ReMBo(Reduce MMV and Boost)的算法,该算法通过将一维随机向量与采样值矩阵相乘,将多测量模型转为单测量模型,然后再利用压缩感知中的恢复算法求解最优稀疏解,可以有效提升恢复速率。文献[5]中提出RSMV(Reduced Single Measurement Vector)模型,该模型通过把压缩采样值矩阵按行加为一列的方式来实现降维,并且利用OMP 算法结合频谱切片的分布特性成功恢复出频域支撑集。但是这两个算法都会减少信号的信息,进而降低信号的重构率。文献[6]使用特征值分解达到降维的效果,转换为多测量向量MMV(Multiple Measurement Vector)。虽然在一定程度上抗噪,但实时性较差。如何有效减少信号恢复时间,又能不影响对信号的感知能力是本文的主要技术关键。因此,本文提出一种基于MWC 的多测量向量模型,简称为RMMV(Reduced Multiple Measurement Vector)模型。将采样值矩阵按行加为多列得到新的采样值替换矩阵,这里的采样矩阵的列数会对后端恢复率和恢复时间有比较大的影响,所以要适当地选择合适的列数。最后利用压缩感知中的OMP 恢复算法找到信号的频域支撑集。
1 MWC模型
MWC 针对的是稀疏宽带多子带信号x(t)[6],其傅里叶变换X(f)带限于F=(-fNyquist,fNyquist),信号模型如图1所示,在F 范围内,一共存在N 个不相交的稀疏子带,其中最大子带带宽为B。

图1 多频带稀疏信号频谱图
MWC 原理框图如图2 所示,每个采样通道都经过伪随机混频、低通滤波和ADC 均匀采样三个过程才能得到压缩采样数据。其中,混频器和低通滤波器必须严格满足设计需求,才能使各个子频带在整个频域内扩散,并且能在期待的基带范围内搬移形成混叠。伪随机信号 pi(t)的循环频率 fp=1/Tp决定了频段分割、搬移的带宽大小,而低通滤波器的截止频率与低速ADC的采样频率 fs=1/Ts相关。

图2 MWC原理框图
伪随机序列 pi(t)是以M 为间隔变化±1 交替变换的序列,目的是使原稀疏多子带信号频谱扩展至整个频带中,pi(t)是周期信号,满足 pi(t+nTp)=pi(t)。对于第i 个通道,其傅里叶展开式为:

其中傅里叶系数有如下表达式:

则经过混频后信号的频域傅里叶变换可表示为:

经过低通滤波器后,保留低频部分的全局频谱切片,然后进行低通采样,则第i 个通道的压缩采样序列yi[n]的离散时间傅里叶变换表示为:
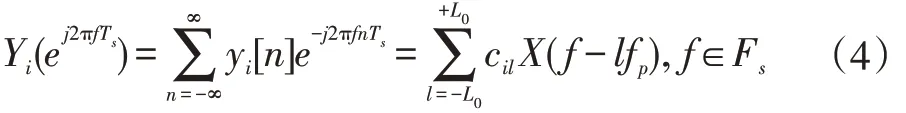
这里的L0是在频率Fs范围中包含所有非零频谱切片的最小整数值,可以通过以下公式计算:

其中 fNyquist表示信号的奈奎斯特带宽,fs为系统对信号的采样率。
2 基于RMMV的恢复算法
RMMV 算法的核心是将压缩采样值矩阵y[n]按行均匀加为k 列,得到一个新的采样值矩阵Vˉ,如果能够证明新的采样值矩阵Vˉ不改变信号的支撑集,则说明RMMV 算法是可行的。
假设 yi[n] 是第i 个通道的采样值,则把 MWC y[n]=Az[n]转化为矩阵形式:


得到新的第1 个通道的压缩采样值:

将m 个通道的压缩采样值都加为k 列,可以得到:

这就是我们得到的新的RMMV 模型,其压缩感知形式为:

在文献[6]提到采样值经过特征值分解降维后有比较好的抗噪性能,而本文的RMMV 算法没有经过特征值分解部分,抗噪性能有所下降。在图1 的MWC 频谱图中,由于 fp≤B,信号的整个频谱被平分为L 个频谱切片后,每个子带的频谱一般占据两个切片,而且某一部分的频谱切片所占能量较多,而占用能量较小的切片位置会受到噪声影响导致丢失,在一次迭代中就能找到最大频谱切片的位置以及其对称频带位置,并且可以将它相邻左右的频带位置加入到支撑集中。具体的RMMV 恢复算法流程如下:
输入:将y[n]按行相加为k 列作为测量值矩阵Vˉ,残差 R 为 Vˉ,测量矩阵 A,索引值向量 Sˉ为[],设置初始迭代值t 为0,原信号稀疏度为K=N;
步骤2:接着找到λt的对称频谱位置以及它们的相邻频谱切片索引值加入到索引值向量Sˉ中;
步骤3:根据索引值向量Sˉ中的值把对应的测量矩阵A 中的列取出组成矩阵ASˉ,并求出其伪逆
步骤 5:更新残差 Ri=R-A×,t++ ;
步骤6:如果t ≥K 或残差Ri满足停止迭代的条件,停止迭代,否则返回步骤1。
输出:支撑集的索引值向量Sˉ
在步骤2 中,这里的选择索引值的方法是求得残差与测量矩阵最大内积的索引值,然后找出其对称位置的索引值,最后把它们相邻索引值都加入到索引值向量中,这样可以快速找到所有的索引值,节省了恢复时所需时间,这种把相邻频谱切片位置加入到支撑集有利于提高RMMV 恢复算法的鲁棒性。
3 数值仿真实验

为了体现抗噪性能,在原始信号中加入高斯白噪声。其中子带数N 为6,能量系数Ei={1,2,3},时间延时τi={0.4,0.7,0.9}μs,子带带宽 B=50MHz,子带载频 fi为[0.5GHz]内的随机值。
实验仿真了不同列数下的RMMV 算法与原MMV算法在恢复性能上的比较,如图3 所示,通道数为50,信噪比从-10dB 到25dB,图中RMMV(k)表示将采样值矩阵降维至k 列,从图中可以看出,RMMV 算法在采样值矩阵列数为2 时,其对信号的恢复率在低信噪比下低于原始MMV 方法,因为原方法经过了特征值分解的部分,这部分有降噪的功能,能有效提高恢复性能,而将采样值矩阵降为2 列会严重破坏原始信号的信号特征,将有效的信息丢失,造成恢复过程对噪声较为敏感。但是信噪比达到4dB 后,恢复性能就与原方法差不多,甚至比原方法的恢复率要高一些。但对于列数大于等于4 时,RMMV 算法在不同信噪比下对信号的恢复率均高于原MMV 方法,可见,列数的增加可以有效提高算法的抗噪性能,但是列数不能无限增加,这样会增加后端的计算负担,因此,对采样值矩阵降维选择合适的维度有利于提高恢复准确性和恢复速率。
为了检验我们提出的RMMV 算法在恢复速率上的性能,把压缩采样值矩阵y[n]加为4 列、6 列和8 列以后,我们对此与原MMV 算法进行了对比仿真实验,如下图所示,通道数m 从 20 到 50,信噪比 SNR 为30dB。从图中可以看出RMMV 算法降维后的列数越少,信号的平均恢复时间越少,大幅度地提升了恢复速

图3 不同信噪比下算法恢复对比图

图4 不同算法的恢复时间对比图
仿真实验的原始信号是宽带稀疏多子带调制信号x(t),其信号的时域模型表示为:度,此外,RMMV 算法中当对采样值压缩为8 列时,其平均恢复时间仍然大大低于原MMV 算法。因此,针对需要快速恢复支撑集的场景,我们所提出的RMMV 算法具有较大的优势,具有较好的实时性,可应用于跳频信号检测。
4 结语
本文首先介绍了用于实现频谱感知的MWC 体系,接着,详细介绍了RMMV 算法模型,这个算法是把压缩采样值矩阵y[n]通过加为k 列的方式跳过了特征值分解部分,也分析了如何选择合适的k 来达到恢复时间和恢复成功率之间的平衡。这个算法可以有效降低CTF 恢复时间,还可以通过控制k 的取值在一个比较低的范围,减少参与后端恢复的Vˉ矩阵的列数,进一步降低算法的运行时间。最终实验验证了RMMV 算法确实可以消除通道对恢复时间的影响,还在一定程度上提升恢复速率,对恢复成功率也有一定的提升效果。

