基于核主成分分析和朴素贝叶斯的滚动轴承故障诊断
朱兴统
(广东工业大学自动化学院,广州510006)
0 引言
滚动轴承作为旋转机械设备中的一个重要组成部件之一,如果滚动轴承出现了故障,就会可能直接影响机械设备的性能,影响生产产品的质量,也可能会导致整台机械设备停止运行。据有关统计,旋转机械故障有大约30%是由于滚动轴承故障引起。有必要对滚动轴承振动信号进行监测,以便及时诊断出故障。因此对滚动轴承故障诊断的研究具有重要的现实意义。在故障诊断过程中,从滚动轴承振动信号中提取各种特征信息是故障诊断的关键环节,能否提取出有效特征信息直接影响故障诊断准确率。机械故障特征提取与故障识别已经成为研究热点领域,有很多研究者提出了许多种故障特征提取与诊断的方法。何斌等人为了提高滚动轴承故障准确率,通过构造相应的小波基函数,采用最小二乘拟合法构造预测器和更新器,应用于对滚动轴承的振动信号进行分析,取得了较好的结果[1]。吴强等人提出结合连续小波变换和独立分量分析的方法对单通道信号的滚动轴承故障进行早期故障[2]。Rajeswari等人提出了一种基于小波包变换和多分类支持向量机的滚动轴承状态诊断方法[3]。针对滚动轴承的故障振动信号具有非平稳性的特点,Yang等人提出了一种基于经验模态分解(EMD)能量熵的滚动轴承故障诊断方法。利用EMD提取不同频段能量作为特征的神经网络诊断方法能够准确、有效地识别滚动轴承故障模式,具有较好的诊断效果[4]。杜振宁和向春枝提出了小波包分解和高阶累积量对轴承振动信号进行特征提取,并通过主成分分析法对特征数据进行降维,利用神经网络算法进行故障分类[5]。Li Meng采用主成分分析(PCA)和支持向量机(SVM)方法对滚动轴承故障模式进行识别。根据振动信号的特点,利用主成分分析(PCA)得到特征向量,利用SVM故障分类器对滚动轴承进行故障诊断。理论和实验表明,该方法在故障模式识别中是可行的[6]。为了提高滚动轴承故障诊断的准确率,本文提出结合经验模态分解、样本熵、核主成分分析和朴素贝叶斯算法的故障诊断方法。
1 振动信号特征提取
1. 1 经验模态分解(EMD)
经验模式分解是一种信号处理的时频分析方法,在非线性、非稳态的信号处理方面具有显著的优势。该方法对信号进行自适应分解是依据该信号数据序列的时间尺度特征来进行的。EMD实际上就是将一个复杂的信号分解为若干个本征模态函数IMF(Intrinsic Mode Function)分量和一个残余分量。IMF需满足两个条件:①函数在时域范围内,局部极值点和过零点的数量必须相等,或者最多相差一个;②在任意时刻点上,局部最大值的包络和最小值的包络的平均值必须等于零。经验模式分解步骤如下:
(1)找出原始信号x(t)中所有的局部极大值和极小值,采用三次样条插值函数分别对局部极大点和局部极小点进行拟合得到上包络线和下包络线。
(2)计算上包络线 bmax(t)和下包络线 bmin(t)的平均值 m(t),将原始信号 x(t)减去 m(t)得到新的信号h(t),即:h(t)=x(t)-m(t)。
(3)判断新的信号h(t)是否满足IMF条件。如果满足条件,则h(t)为第一个IMF分量;如果不满足条件,将 h(t)作为原始信号,重复步骤(1-3),直到得出第一个IMF分量,记为c1(t)。
(4)将原始信号 x(t)减去第一个 IMF 分量 c1(t),得到新信号r1(t),即:

(5)将 r1(t)作为原始信号,重复步骤(1)到(4),如果rn(t)为单调函数,则终止上述步骤。最终将原始信号x(t)分解得到n个IMF分量和一个残余量rn(t),即:

1. 2 样本熵
样本熵是RICHMAN等提出的一种时间序列复杂性的度量方法[7]。样本熵是近似熵的改进算法,但其精度比近似熵更高。设时间序列X有N个数据点,样本熵的计算步骤如下:
(1)依据原始时间序列构造出m维向量,得到N-m+1个m维向量:

(2)Xm(i)与Xm(j)分别是上一步骤构造的m维向量,Xm(i)与Xm(j)之间的距离d[Xm(i),Xm(j)]定义为两者对应元素差值的绝对值的最大值,即:

(3)假设相似容限为r,对于给定Xm(i),计算Xm(i)与其余向量 Xm(j)(j=1,2,…,N-m;j≠ i)的距离d[Xm(i),Xm(j)],统计满足条件d[Xm(i),Xm(j)]≤r数量,设为Ai,并求出Ai与N-m的比值,记作,即:


(6)理论上,原始序列的样本熵定义为:
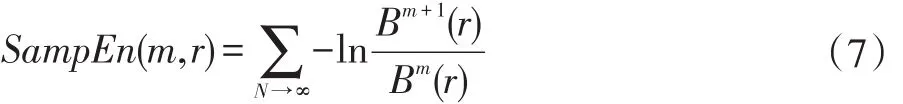
当N为有限数时,上式表示成:
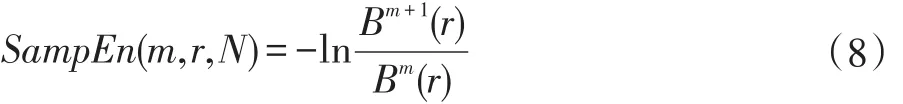
1. 3 核主成分分析(Kernel Principal Component Analysis)
主成分分析(Principal Component Analysis,PCA)是一种统计分析方法,可以用于减少数据集的维数的一种方法,被广泛应用于信号处理、模式识别、故障诊断等领域。主成分分析不能处理非线性数据,而故障诊断应用中所收集到的振动信号数据大部分都是非线性的。Scholkopf等人在主成分分析方法引入核函数,提出了核主成分分析方法[8]。核主成分分析实际上就是先通过非线性映射函数将输入数据空间映射到高维特征空间,然后进行主成分分析。
对于输入空间中的m个n维数据样本xi∈Rn,对其进行非线性映射Φ:Rn→F得到高维的特征空间。假设高维的特征空间的样本满足中心化条件:,则高维的特征空间的样本协方差矩阵为:

为了求解协方差矩阵的特征值与特征向量,假设特征值λ≥0,特征向量V∈F{0},满足:

由式(10)中两边分别左乘Φ(xk),有:
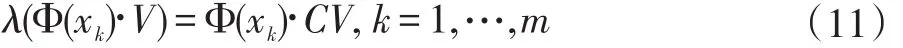
特征向量V可以由Φ(xi)线性组合表示为:

式中,Φ(x)=(Φ(x1),…,Φ(xm)),ai为相关系数,α=[α1,…,αm]T。
把式(12)代入式(11),可得:
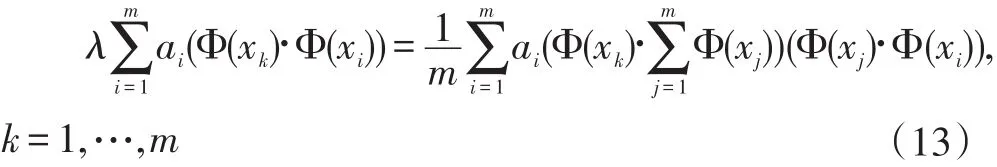
定义一个m*m的矩阵K:

式(13)可写成:

式中K为对角矩阵。
式(15)两边同时去除K,有:

求解核矩阵K,将特征值从大到小排列,取排列在前面的 p个特征值为:λ1,λ2,…,λp,对应的特征向量为:a1,a2,…,ap,并归一化特征向量,有:

对于给定一个测试点x∈Rn在V上的映射为:
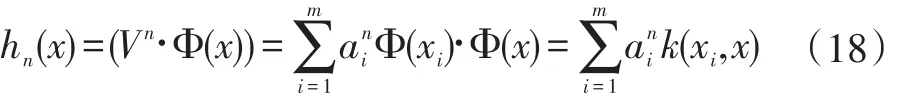
2 朴素贝叶斯
假设数据集有n个特征属性,类别标签集合为{c1,…ck}。某个待分类样本X={X1,X2,…,Xn}。根据贝叶斯定理:

P(ci)是先验概率,可以根据训练集计算出来。
由于朴素贝叶斯假定样本的各个特征属性对样本分类结果的影响是相互独立的,所以条件概率为:
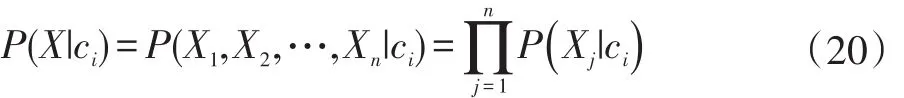
将式(20)代入式(19)得:

由于对所有的类别P(X)都相同,所以公式(21)只需考虑分子部分。
朴素贝叶斯分类器可表示为:
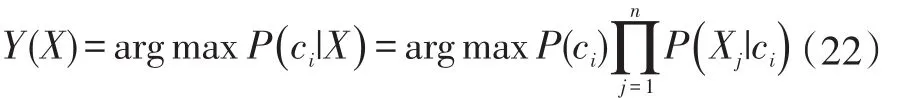
对P(Xj|ci)的求解,有三种常见的模型:多项式模型、高斯模型、伯努利模型。本文采用高斯模型求解,高斯模型公式为:
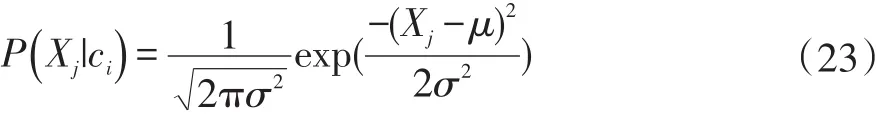
3 故障诊断流程
基于经验模态分解样本熵和朴素贝叶斯的故障诊断流程如图1所示,具体流程步骤描述如下:
(1)采集轴承振动信号数据。
(2)采用经验模态分解对振动信号进行分解,并计算各模态分量。
(3)计算各模态分量的样本熵,构建特征向量,分为训练样本集和测试样本集。
(4)朴素贝叶斯分类。用训练样本集对朴素贝叶斯分类器进行训练,测试样本集输入素贝叶斯分类器进行诊断。
(5)输出诊断结果。

图1 故障诊断流程
4 实验
本实验采用美国凯斯西储大学轴承数据中心的轴承故障数据集。该轴承故障试验台如图2所示,该试验台主要的组成部件有:一个1.5KW的电动机、一个扭矩传感器/译码器、一个功率测试计、电子控制器等。驱动端的轴承为SKF6205,驱动端的轴承座上方安装有一个加速度传感器,通过这个加速度传感器来采集轴承的振动加速度信号,采样频率为12kHz。以2048个数据点为一组样本,分别选取内圈故障、外圈故障、滚动体故障、正常状态的轴承振动信号各50组,总共200组。

图2 美国凯斯西储大学轴承数据中心的轴承故障试验台
本实验从每类样本中随机选取40组的样本作为训练集,10组样本为测试样本集。图3为内圈故障、外圈故障、滚动体故障、正常状态各一组轴承振动信号样本的时域波形。
滚动轴承振动信号通过EMD进行分解,取前7个IMF分量计算样本熵,构成7维的特征向量,部分样本熵数据如表1所示。然后,利用KPCA对7维的特征向量进行降维,得到2维的特征向量,作为朴素贝叶斯分类器的输入向量。最后将2维的特征训练集对朴素贝叶斯模型进行训练,将2维的特征测试集输入到训练后朴素贝叶斯模型得到故障诊断结果。为了验证本文方法的有效性,将本文方法与小波包+能量+朴素贝叶斯、EMD+样本熵+朴素贝叶斯方法对比,三种方法的故障准确率如表2所示,本文方法的故障准确率为95%,分别高于另外两种方法7.5%和2.5%。
5 结语
本文提出的基于经验模态分解、核主成分分析和朴素贝叶斯算法的故障诊断方法。利用经验模态分解对滚动轴承存在复杂、非线性、非平稳的振动信号有明显的优势。利用核主成分分析将非线性的样本信息映射到高维的空间,再利用高维空间进行线性降维,消除一些不重要的属性,可以提高故障诊断效率。朴素贝叶斯模型具有算法较简单,且有稳定的分类效率。融合经验模态分解、核主成分分析和朴素贝叶斯算法的优点,能够有效解决滚动轴承故障诊断问题。

图3 原始轴承振动信号的时域波形

表1 滚动轴承各状态下的EMD样本熵

表2 三种方法的准确率对比

