考虑非均质性的致密储层改造效果评价

郭 昊，魏 旭，张永平，王海涛，邓大伟，朱兴旺

（1.东北石油大学石油工程学院，黑龙江大庆163318；2.中国石油大庆油田有限责任公司采油工程研究院，黑龙江大庆163454）

致密储层的低渗透特性使其无法在钻完井之 后直接投入生产［1］，需要采取适当的增产措施。提升水平井钻井技术［2］以及采取水力压裂增产措施是提升该类储层产能的重要方法［3-8］，有必要对其进行深入研究。水力压裂技术的研究方法主要包括3方面：理论研究、实验研究以及数值模拟研究。较常见的数值模拟方法包括边界元法、有限元法、有限差分法以及离散元法等。CHEN等［9］应用有限差分法解决断裂力学问题。有限元法也能够解决裂缝问题，许多基于有限元的方法已被开发用于解决这类问题，例如具有自适应网格的常规有限元法［10］、粘结单元法［11］、节点力释放法、嵌入式不连续法［12］和扩展有限单元法等［13］。这些方法主要是将裂缝模型嵌入网格中，但在处理裂缝延伸时有很大难度。因为常规有限元法不能描述单元内的不连续表面，裂缝必须沿着单元边界或给定的路径延伸，在一定程度上限制了裂缝的延伸。这些数值模拟方法有个共同点，就是需要划分网格。但在求解过程中的网格变形、沙漏效应严重影响计算结果的准确性。

物质点法（MPM）是一种无网格数值模拟法，用来解决动态固体力学问题。它可以用来代替传统的动态有限元法。在MPM中，将材料离散为一组质点。背景网格与质点相关联，由网格控制边界条件，背景网格只是作为计算工具，质点信息与背景关联，在每一个时间步长内求解动量方程。方程式求解成功后，基于所有的质点属性如位置、速度、加速度和应力状态等，对网格进行更新。MPM结合了拉格朗日（质点）和欧拉（网格）的优点，已证明可用于解决裂缝延伸问题，包括在塑性或粘性变化影响下的大应变或旋转。但目前该方法很少用于水力压裂方面的研究。在考虑储层非均质性的基础上，对大庆油田某地区致密储层水平井的改造效果进行评价分析，模拟结果与井下微地震监测情况进行对比，以验证所提出方法的准确性。

1 物质点方程

1.1 控制方程

假设区域Ω受牵引力和位移边界条件的影响，其控制方程为［14］：

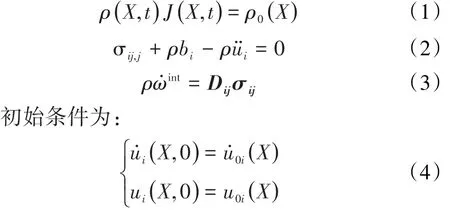
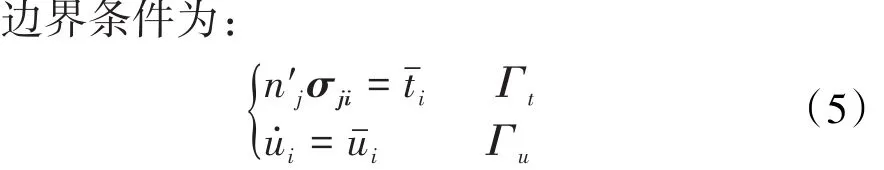
压裂液在储层中的流动满足质量守恒方程，即（1）式。

以虚拟位移δu（iδui|Γu=0）为测试函数，动量方程（2）和牵引边界方程（3）的弱形式为：

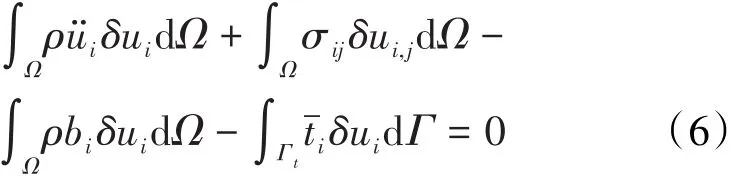
在断裂力学中，主要的问题是对裂缝应力场进行分析。为了表征裂缝尖端的应力场各向异性，并预测裂缝的延伸情况，假设裂缝延伸过程中能量是均衡的，能量释放率控制裂缝的延伸。当能量释放率超过临界韧性（裂缝表面吸收能）时，裂缝延伸。在物质点法中，根据局部应力和裂缝面的J积分来计算能量释放率［15］，J积分表达式为：

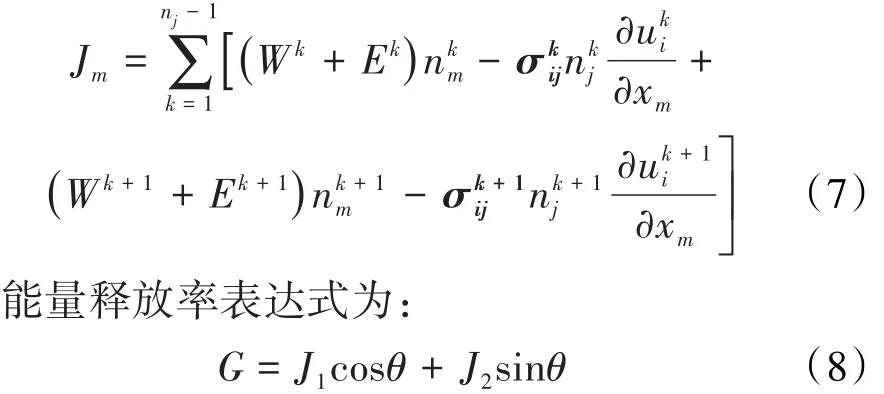
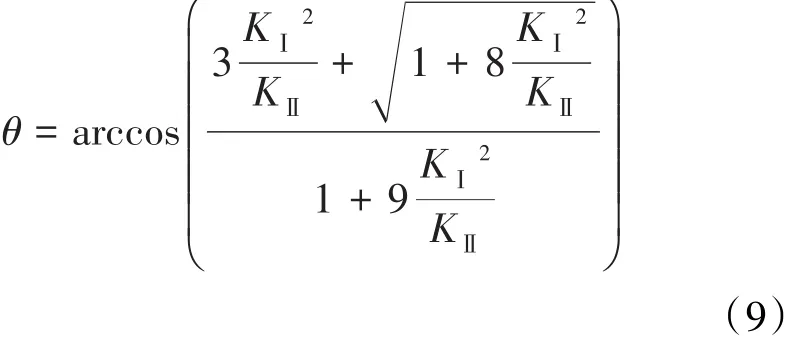
假设人工压裂的裂缝延伸角度主要受最大水平主应力方向的影响。该假设基于物体在剪切力方向上阻止裂缝形成，使得裂缝走向发生变化，形成Ⅰ型裂缝。基于这个理论，裂缝走向与水平轴夹角的表达式为：

1.2 方程离散及求解

在求解动量方程时，质点和背景网格完全固定连接，随背景网格一起运动，因此可通过建立在背景网格节点上的有限元形函数N（Ix）i来实现质点和背景网格节点之间信息的映射。用带有下标I的量来表示背景网格节点的变量，用带有下标p的量来表示质点携带的变量，则质点p的位移uip可以由背景网格节点的位移uiI插值而得到，即在MPM中，区域Ω被离散化为质点集合，并且背景网格用于求解动量方程。在每个时间步中，质点都附着在背景网格上。因此，可以通过内插网格节点位移来获得粒子位移，其表达式为：

以弱形式（6）中的粒子作为正交点，应用虚拟位移（δuiI）可得到背景网格节点动量方程为：

采用中心差分法［16］求解背景网格结点动量，可得tn+1/2时刻的背景网格结点动量为：

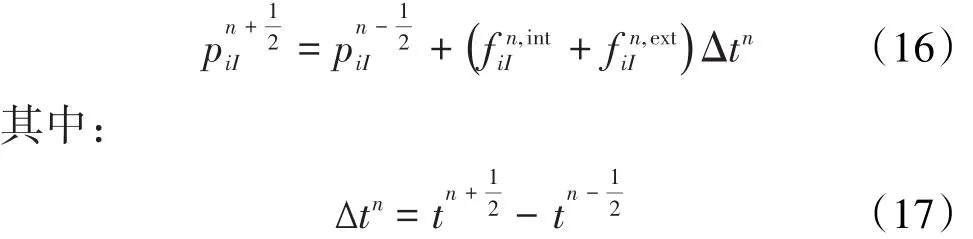
通过背景网格形函数将积分结果映射回质点以更新质点的位置和速度，即分别利用背景网格的加速度场和速度场更新质点的速度和位置，则：

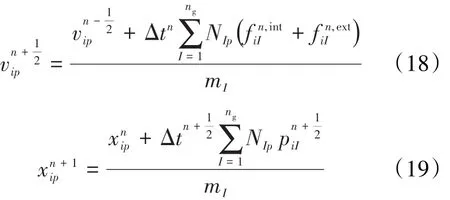
2 储层改造效果评价模型的建立及分析

2.1 模型的建立

根据已完钻水平井的井眼轨迹，选取参数包括：储层渗透率为0.29 mD，泄流面积为100 000 m2，杨氏模量为55 GPa，泊松比为0.26，岩石密度为2.60 g/cm3，断裂韧性为15 J/m2，最大水平主应力为50 MPa，最小水平主应力为40 MPa，各向异性系数为1.08，水平井与南北夹角为45°，施工排量为10 m3/min，最大加砂浓度为25%。基于物质点法，建立储层改造效果评价模型（图1）。通过求解动量方程（（2）式），利用背景网格的加速度场和速度场更新质点的速度和位置（（18）式和（19）式）来计算裂缝的延伸情况。根据J积分计算结果，即（7）式和（8）式，确定压裂裂缝附近产生的应变，从而对储层改造效果进行评价。

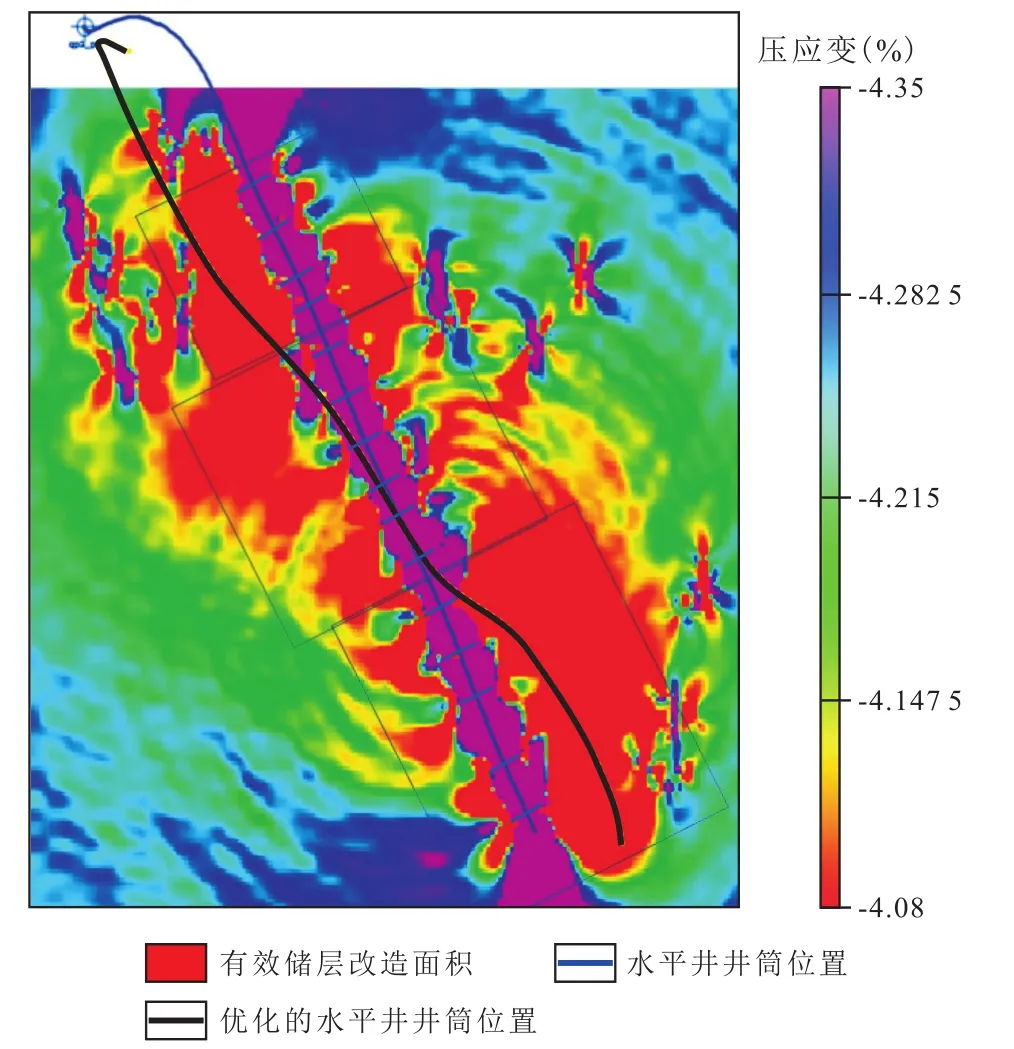
图1 储层改造效果评价模型Fig.1 Schematic of the mathematical model to evaluate the formation stimulation

2.2 压裂施工段数

目前为止，压裂施工段数的选取并没有一个统一的标准，所建立的储层改造效果评价模型考虑了地质参数与施工参数，最大可能地还原储层真实情况，从而需要对压裂施工段数进行优化。由压裂施工段数对储层改造面积的影响（图2）可见，储层改造面积比例随着压裂段数的增加而逐渐增加，但整体上升趋势逐渐减缓，当压裂段数达到15段时，继续增加压裂段数，储层改造面积的比例提升不再明显。由储层改造面积增长比例（图2b）可见，压裂段数从10段增长到12段时，增幅比例较大且保持在0.04，这表明，该储层条件下，若采用小于12段压裂，会严重限制储层改造效果的提升。当压裂段数超过12段时，储层改造面积的增长比例持续下降，达到15段后继续增加压裂段数，其储层改造面积增幅比例小于0.01。结合图2a和2b可最终得出，该井选取15段压裂较为合理，此时储层改造面积比例为0.87。

2.3 裂缝形态

在考虑储层非均质性的情况下，由水平井井筒左右两侧裂缝半长与设计裂缝半长的对比（图3）可以明显看出，左右裂缝半长相差很大，裂缝半长的整体变化规律与储层改造面积的变化规律基本相同，在假设为均质的前提下，该区块的研究结果会与实际情况产生严重的偏离。对于6—10段较均质的储层，其裂缝半长均小于设计裂缝半长，产生这种情况的主要原因是对于非均质储层，水平井井筒一侧裂缝可能很难有效延伸，使得地面注入的压裂液流向更容易产生裂缝的另一侧，从而产生一侧裂缝半长特别长，另一侧裂缝半长较短的情况；而对于储层较为均质的情况，能量均匀分布在水平井井筒两翼裂缝缝尖上，因此两翼裂缝半长很相近，裂缝半长与设计半长相近。

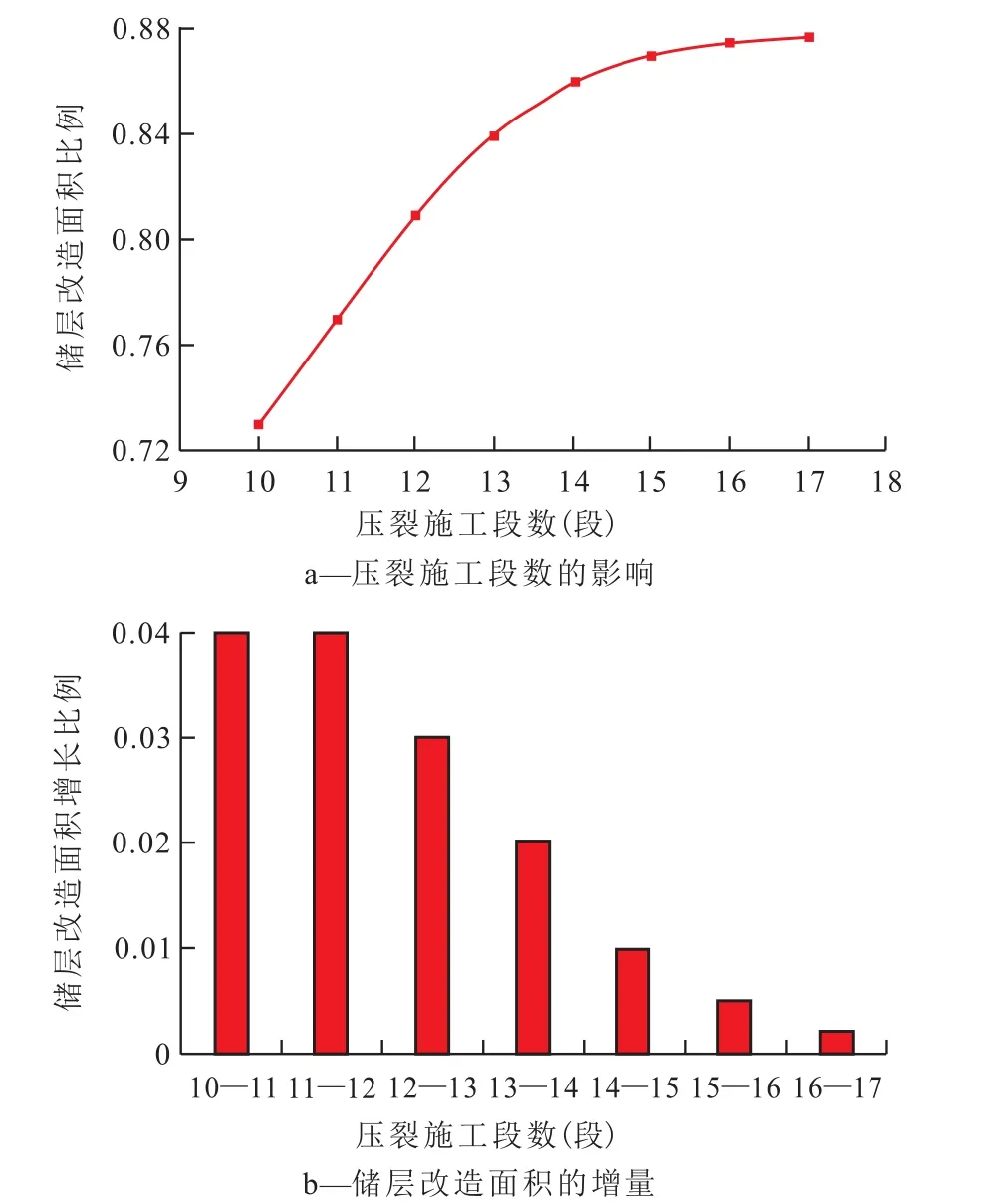
图2 压裂施工段数对储层改造面积的影响Fig.2 Influence of the number of fracturing stage on the stimulated reservoir area

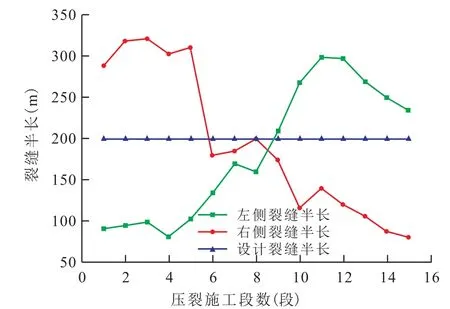
图3 考虑非均质性的水平井井筒两侧裂缝半长分布Fig.3 Distribution of fracture half-length on two wings of horizontal well in the consideration of heterogeneity

2.4 储层改造效果

压裂施工能有效增加储层的改造面积，最终提升油气井的产量。而对储层改造效果一直缺乏合理准确的评价方法。根据所建立的储层改造效果评价模型，对15段裂缝的改造效果进行评价。因为模型考虑储层非均质性，所以对水平井井筒左侧和右侧的储层改造情况分别进行研究。1—5段两翼不对称，东侧改造效果好；6—11段两翼较为对称，但西侧改造效果好于东侧；12—15段西侧改造效果好（图1）。由图4可见，6—10段水平井井筒左右两侧的储层改造面积相差不大，表明6—10段附近区域储层较为均质。1—5段和11—15段水平井井筒左右两侧的储层改造面积差距很大，表明储层非均质性强。对于强非均质储层采用均质模型进行计算，结果会存在很大误差。应用所建模型可知，如果在左右两侧储层改造面积相同的部位（图1中的黑色实线）布置水平井井筒，则其左右两侧近似为均质情况，可避免储层非均质性对储层改造效果的影响，使储层改造效果得以改善。

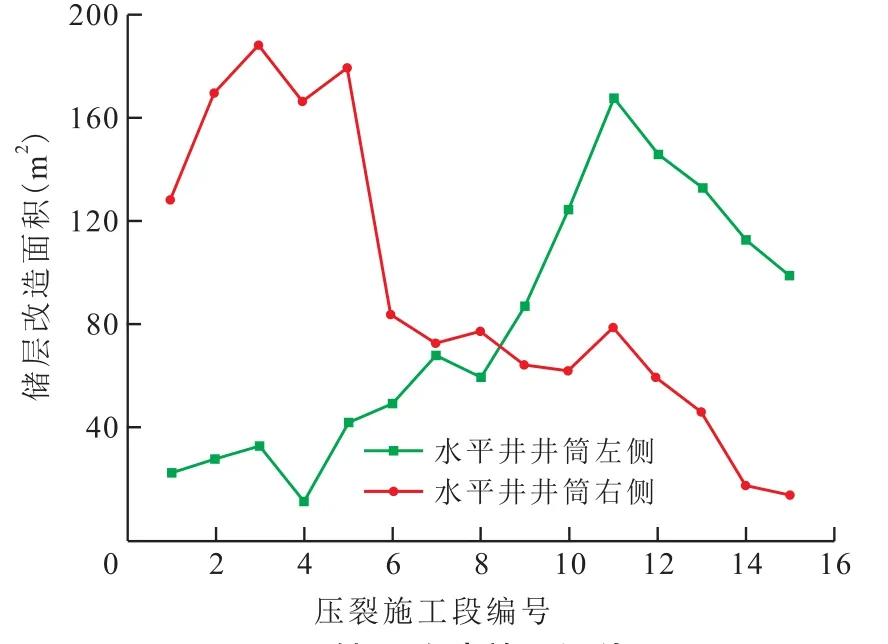
图4 储层改造效果评价Fig.4 Evaluation of the formation stimulation

为进一步对储层的非均质性进行研究，选取非均质性较为严重的1—5段进行详细分析，应用（7）式分别计算1—5段的J积分变化情况（图5）。J积分是与裂缝延伸路径无关的积分，主要表示裂缝尖端产生的应变场的平均值。由图5可见，无因次时间小于0.5时，J积分的值为0。当无因次时间达到0.5时，J积分的值开始逐渐增加。J积分的值从大到小排序为第3段、第5段、第2段、第4段及第1段。与5段裂缝的储层改造面积（左右裂缝半长的改造面积之和）的大小排序相同。这表明可以通过计算J积分的大小来比较各压裂段之间的储层改造效果。每段的J积分曲线波动情况不同且均出现无规律的增减，水平井井筒两侧的储层改造面积之差越大，储层非均质性越强，J积分曲线波动越明显。产生这种情况的主要原因是由于水平井井筒一侧相对容易产生应变而另一侧相对困难，导致能量分布不均匀，J积分变化无规律。因此，可以根据J积分曲线的复杂程度，评价储层的非均质性。

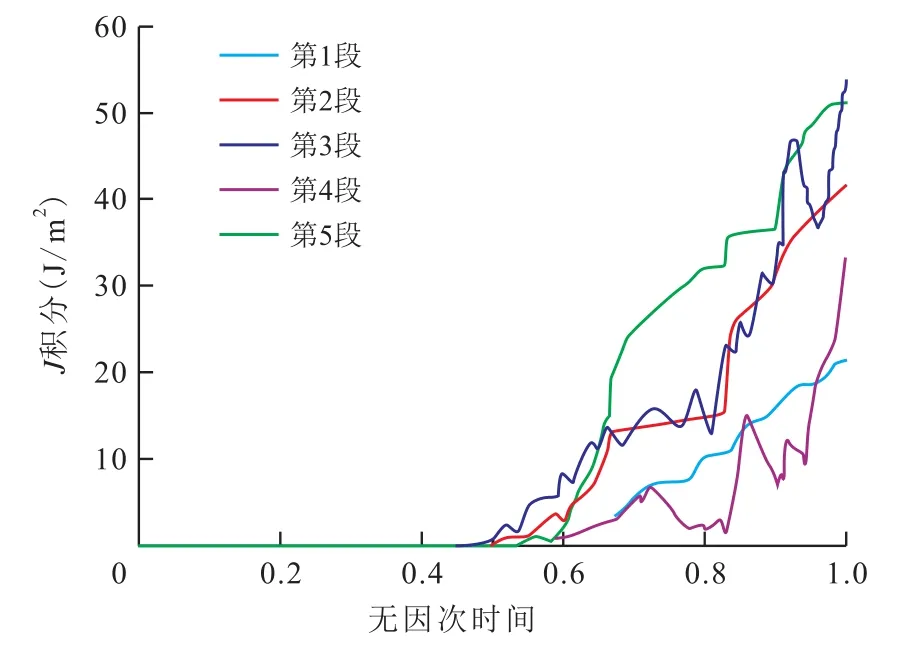
图5 J积分变化情况Fig.5 Changes of J integral

2.5 模型验证

为了验证所建数值模型的准确性，将差应力场模拟情况与微地震检测信号进行对比（图6），差应力场与微地震检测信号一致，储层非均质性较强的1—5段（图6a和6b中黑圈部分），其相似度仍然很高，因此，所建非均质模型的计算结果准确，与实际情况相似度很高，适合作为该类非均质储层的数值模型。

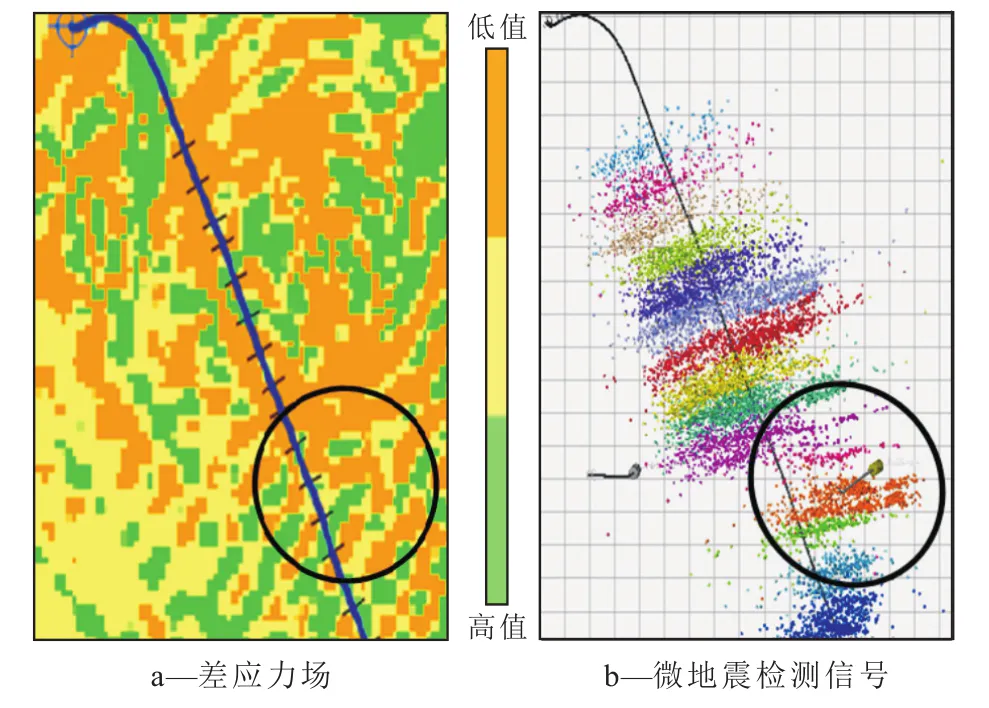
图6 差应力场与微地震检测信号对比Fig.6 Comparison between in-situ differential stress field and microseismic detection signal

3 结论

根据物质点法特性，建立非均质储层改造效果评价模型，对储层改造效果进行分析，并对压裂施工段数选取情况进行研究。最终可以得到如下结论：①压裂过程中，储层的非均质性必须考虑，所建模型能有效预测及评价储层改造效果。②通过计算J积分，可以比较各段储层改造面积，并且可以根据J积分曲线的复杂程度，评价储层的非均质性。③压裂施工段数在一定程度上可以增加储层的改造面积，但是当段数达到一定程度时，储层改造面积增幅显著降低。④不考虑储层非均质性，会严重降低储层改造效果，且水平井井筒两翼裂缝半长分布不均匀。

符号解释：Ω——区域；ρ——密度，kg/m3；X——拉格朗日坐标；t——当前时间，s；J——雅可比行列式；ρ0——初始密度，kg/m3；σij,j——柯西应力，Pa；bi——单位质量的体力，N/kg；i——加速度，m/s2；下标 i，j——爱因斯坦公式中空间变量的分量；ω˙int——单位质量的内能，J；Dij——变形率张量，m；σij——ij方向的柯西应力张量，Pa；——物质点速度，m/s；u˙0i——初始速度，m/s；ui——物质点位移，m；u0i——初始位移，m；n′j——无因次单位外法线方向；σji——ji方向的柯西应力张量，Pa； ˉti——面力，N；uˉi——质点边界速度，m/s；Γt和Γu——Ω的无因次牵引边界和位移边界；δ——Dirac函数；ui,j——质点在爱因斯坦公式中空间变量的分量位移，m；Γ——围绕裂缝尖端的任意积分轮廓；Jm——J积分，J/m2；m——其值为1，2，分别表示水平井井筒左侧和右侧；k——积分点，个；nj——积分点总数，个；W——通过积分dW=σijdεij得到的应力功密度，J/m2；εij——应变；E——动能密度，J/m2，其值为2；nm——围绕裂缝尖端的任意积分轮廓（Γ）或围绕裂缝尖端的具有最大半径ε的积分轮廓（Γε）单位法向量的第m个分量，m2；xm——质点坐标；∂ui/∂xm——位移梯度；G——能量释放率；J1——水平井井筒左侧J积分，J/m2；J2——水平井井筒右侧J积分，J/m2；θ——裂缝走向与水平轴的夹角，（°）；KⅠ——Ⅰ型裂缝应力强度因子，MPa· m；KⅡ——Ⅱ型裂缝应力强度因子，MPa· m；uip——质点p的位移，m；NIp——在粒子p的位置处评估的节点I的形状函数；uiI——背景网格节点位移，m；下标p——质点；I——网格节点；p˙i——节点动量，kg·m/s；mI——背景网格的总质量矩阵；u¨iI——粒子的加速度，m/s2；fiIint——背景网格节点内力，N；fext——背景网格节点外力,N;p——第I个网格节点在i方iIiI向的动量，kg·m/s；viI——网格节点I处的速度，m/s；np——质点数量，个；mp——背景网格的质量矩阵；ρp——p点密度，kg/m3；NIp,j——p点的形函数；σijp——p点的应力张量，Pa；bip——p点的体力，N；Δtn——时间间隔时刻质点的速度时刻质点的速度，m/s；ng——网格节点的数量，个时刻质点的位置；——tn时刻质点的位置。