页岩储层压裂水平井气-水两相产能分析
李勇明,陈 希,江有适,吴 磊,周文武,刘福建
(西南石油大学油气藏地质及开发工程国家重点实验室,四川成都610500)
水平井分段压裂是页岩储层成功改造的关键技术。中外学者针对压裂后的产能分析建立了大量的数学模型[1-10],描述页岩气的多重运移机理,分析页岩储层压裂后的产气规律;但所建立的数学模型大多考虑页岩气的单相流动,忽略了返排阶段压裂液的存在对产气规律的影响,造成产气量预测结果偏大。现场多数页岩气井都具有较长的产水期,因此,气-水两相渗流数学模型能更准确地描述页岩储层流体的实际渗流状况。ADEFIDIPE等建立了页岩储层水平井气-水两相渗流模型,认为水仅分布于人工主裂缝中,但在实际压裂过程中,由于压裂液滤失,人工主裂缝周围存在侵入带[11]。尹虎等建立了页岩储层气-水两相径向流模型,求解得到生产过程中井底压力的变化规律[12]。王怀龙建立了页岩气的气-水两相产能模型,但模型中未考虑储层应力敏感和页岩气滑脱效应[13]。郭小哲等考虑了页岩气的滑脱效应和应力敏感,但忽略了毛管力的影响[14-15]。基于前人研究成果,笔者建立了综合考虑页岩气吸附解吸、扩散、滑脱、应力敏感、毛管渗吸效应的气-水两相渗流数学模型,分析压裂液返排阶段页岩气藏压裂水平井的产气量变化规律,研究成果对实现页岩储层产能的准确预测具有指导意义。
1 物理模型建立及假设条件
页岩储层压裂后,人工主裂缝周围会产生复杂的裂缝网络[16],即有效改造区域(SRV区)。在压裂和压裂后关井的过程中,压裂液沿着裂缝网络滤失,在人工主裂缝周围形成侵入带,且一部分压裂液自发渗吸进入页岩基质[17]。STALGOROVA等认为,页岩储层压裂后可分为3个区域:未改造区、SRV区和人工主裂缝区[18]。为此,考虑SRV区存在压裂液侵入带,建立物理模型的基本假设条件为:①整个页岩储层为矩形且等厚。②人工主裂缝为对称双翼平面缝,裂缝高度等于储层厚度。③SRV区包含基质和裂缝网络,基质和裂缝网络之间存在窜流,利用双孔双渗模型进行描述。④人工主裂缝区和SRV区的裂缝网络为气-水两相流动,且气体不溶于水。⑤SRV区压裂液未侵入区域的含水饱和度为束缚水饱和度。⑥页岩基质具有超低含水饱和度的特征,且渗透率极低,因此假定基质的含水饱和度仍低于束缚水饱和度,仅存在气体渗流,且相对渗透率为1。⑦未改造区仅存在页岩基质,不考虑压裂液侵入,为单相流动。
2 数学模型建立及求解
2.1 数学模型建立
2.1.1 未改造区的流动
页岩基质为纳米孔隙,综合考虑克努森扩散、气体滑脱效应,得到页岩基质表观渗透率为[19]:

2.1.2 SRV区的流动
根据质量守恒原理,可以得到SRV区裂缝网络中的气相渗流方程为:

由于裂缝网络缺乏支撑剂支撑,存在极强的应力敏感,因此引入指数型应力敏感公式:

2.1.3 人工主裂缝区的流动
人工主裂缝区的气相渗流方程为:

2.1.4 相对渗透率
气-水两相的相对渗透率计算公式为[21]:

由于人工主裂缝的渗透率较高,导致气-水两相干扰较弱,其相对渗透率曲线中的λ取值为1[22];对于裂缝网络,其λ取值为2。
2.1.5 毛管力
由于人工主裂缝的渗透性较好,因此毛管力可以忽略不计。裂缝网络中的毛管力曲线可由经验公式[23]求得:
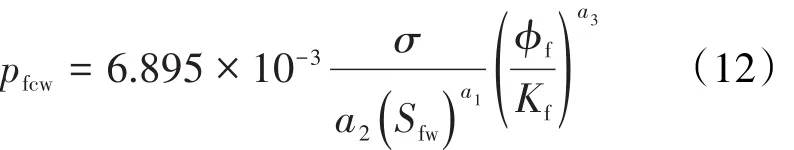
2.2 数学模型求解
将(3)式—(5)式和(7)式—(9)式进行差分离散,分别得到页岩基质系统和裂缝系统的气-水两相渗流微分方程的差分方程组。传导率采用上一时刻的压力和水相饱和度来计算。对于强非线性项,例如相对渗透率、毛管力斜率,采用单点上游加权;其他涉及网格交界处的参数,采用调和平均计算。求解多相流差分方程组常见的方法有IMPES方法和SS方法,其中IMPES方法是先通过隐式求解压力,然后再显式求解相饱和度,这样会造成较大的物质平衡误差。因此,笔者采用SS方法求取压力和相饱和度,即压力和相饱和度联立求解。
3 实例计算及结果分析
以某区块页岩储层压裂水平井为例,基于建立的数学模型,分析裂缝参数、页岩气吸附解吸、毛管力对页岩气产量的影响。页岩储层压裂水平井气-水两相产能模拟所需的相关参数如下:页岩储层的几何参数为800 m×500 m×30 m;温度为365 K,原始压力为30 MPa;页岩基质的孔隙度为0.08,渗透率为0.005 mD;共有3条人工主裂缝,半长为120 m,孔隙度为0.45,渗透率为5 000 mD,初始含水饱和度为0.9;裂缝网络的孔隙度为0.01,渗透率为0.5 mD,束缚水饱和度为0.05;朗格缪尔压力为7.5 MPa,朗格缪尔体积为0.005 m3/kg,井底流压为25 MPa;压裂液侵入深度为10 m,黏度为1 mPa·s,侵入带含水饱和度为0.7;窜流系数为0.5 m-2,气水界面张力为72 dyn/cm。
基于以上参数,分别计算考虑压裂液返排阶段和不考虑压裂液返排阶段的页岩储层压裂水平井产量(图1)。如果不考虑压裂液返排阶段,页岩储层压裂水平井的初期产气量明显偏高。生产初期,由于人工主裂缝及裂缝周围存在大量压裂液,地层中流体流动为气驱水的过程,裂缝中的含水饱和度逐渐降低,日产气量呈上升趋势,并逐渐达到峰值。当人工主裂缝中的含水饱和度降至一定值,随着近井处压力下降,日产气量逐渐降低,400 d后不考虑压裂液返排阶段的日产气量和考虑压裂液返排阶段的日产气量趋于一致。
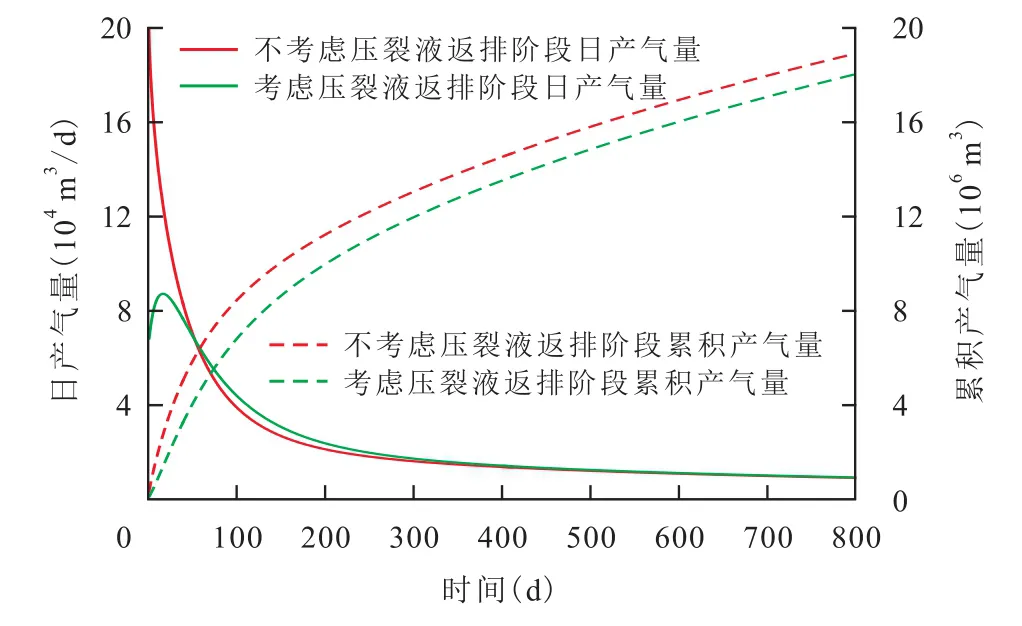
图1 压裂液返排对页岩气产量的影响Fig.1 Influence of fracturing fluid backflow on shale gas production
3.1 裂缝参数对页岩气产量的影响
分析裂缝参数对页岩气产量的影响(图2)发现,裂缝网络渗透率越高,气体越易突破压裂液侵入带,日产气量峰值出现的时间越早,峰值越高,初期产气量越高。当裂缝网络渗透率大于1 mD时,累积产气量增加不明显。人工主裂缝越长,初期产气量越高;因此在进行水力压裂时,应尽可能造长缝。随着人工主裂缝长度(LF)增加,日产气量峰值略有增加,但峰值出现时间略晚;这是因为在压裂液返排过程中气体在近井带发生锥进,人工主裂缝长度对日产气量峰值的影响较小,人工主裂缝越长,裂缝中的压裂液越多,当近井带含水饱和度降低时,裂缝远端有更多的压裂液补充,因此日产气量峰值出现的时间略晚。人工主裂缝渗透率越高,裂缝中的气体和水越容易流动,因此日产气量的峰值越高,峰值出现时间也越早。整体上,裂缝网络渗透率越高,人工主裂缝越长、渗透率越高,初期产气量越高。
3.2 页岩气吸附解吸对页岩气产量的影响
分析页岩气吸附解吸对产气量的影响(图3)发现,在生产过程中地层压力不断下降,页岩气不断解吸,在一定程度上补充了地层能量。当朗格缪尔体积增加时,日产气量峰值增加不明显,其原因为生产初期驱动压裂液返排的气体主要为裂缝网络中的游离气;随着生产的进行,朗格缪尔体积越大,解吸出的页岩气越多,地层压力下降得越慢,因此累积产气量越高。
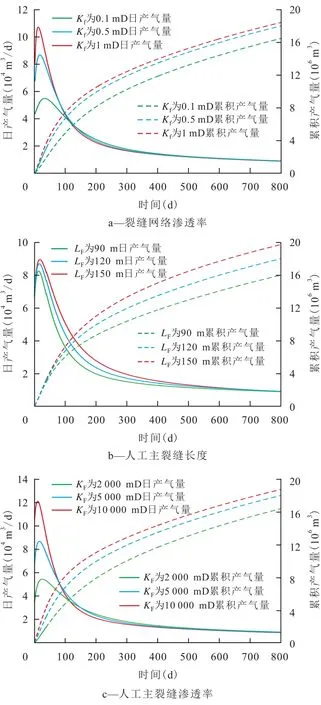
图2 裂缝参数对页岩气产量的影响Fig.2 Influence of fracture parameters on shale gas production

图3 页岩气吸附解吸对产气量的影响Fig.3 Influence of desorption and adsorption of shale gas on shale gas production
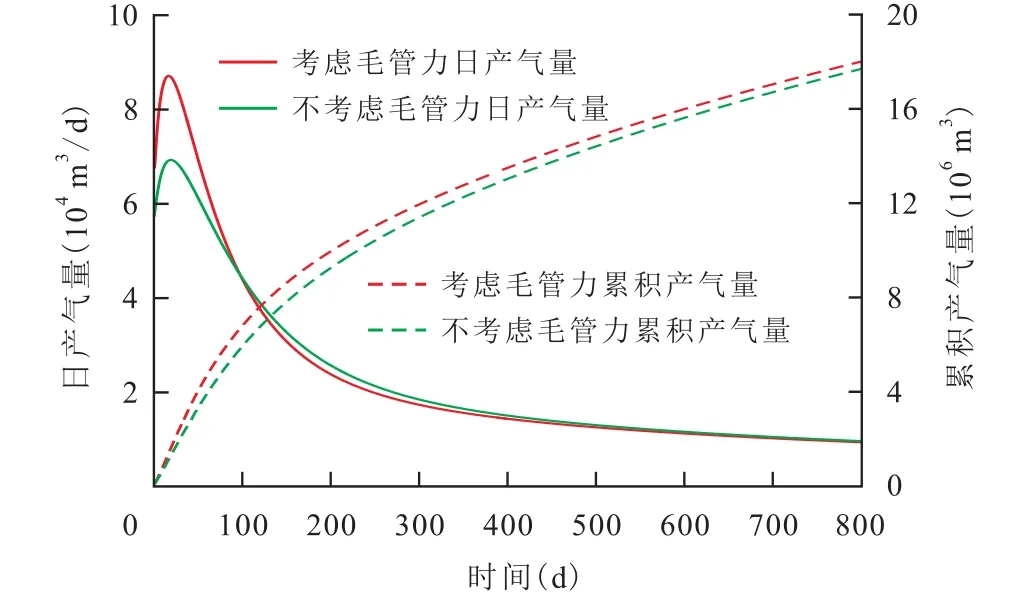
图4 毛管力对页岩气产量的影响Fig.4 Influence of capillary force on shale gas production

图5 裂缝系统含水饱和度分布Fig.5 Water saturation distribution of fracture system
3.3 毛管力对页岩气产量及压裂液返排率的影响
由毛管力对页岩气产量影响的分析结果(图4)可以看出,考虑毛管力作用的初期产气量高于不考虑毛管力作用的初期产气量,且800 d后考虑毛管力作用的累积产气量比不考虑毛管力作用的累积产气量高1.77%。究其原因为毛管力的存在,改变了裂缝网络中含水饱和度的分布状态(图5)。在毛管力的作用下,压裂液在采出的同时,一部分向裂缝网络深部渗吸,导致裂缝周围含水饱和度快速降低,更有利于气体流动,因此初期产气量及产气量峰值均较高。由毛管力对压裂液返排率的影响(图6)可以看出,在毛管力的作用下,大部分压裂液被渗吸进入裂缝网络深部,800 d后压裂液返排率仅为25.2%;而不考虑毛管力作用,800 d后压裂液返排率可达40.3%,这也解释了现场某些页岩气井出现返排率越低、产气量反而越高的现象。
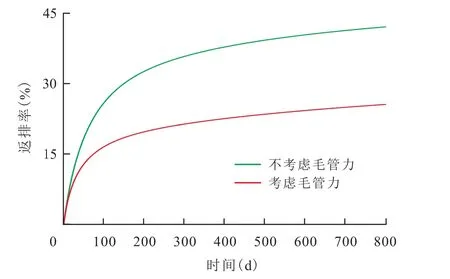
图6 毛管力对压裂液返排率的影响Fig.6 Influence of capillary force on backflow rate of fracturing fluid
4 结论
为研究页岩储层压裂后气-水同流对页岩气产量的影响,建立综合考虑页岩气吸附解吸、扩散、滑脱效应、应力敏感、毛管渗吸效应的双孔双渗气-水两相渗流数学模型,并基于有限差分,采用SS方法求解得到考虑压裂液返排阶段的页岩气产量及地层流体饱和度分布。研究结果表明,在生产初期,由于压裂液返排的影响,日产气量呈先升高后降低的趋势,初期产气量明显低于不考虑压裂液返排所预测的产气量,但后期产气量则基本一致;裂缝网络渗透率、人工主裂缝长度、人工主裂缝渗透率、毛管力是影响页岩气初期产气量的关键因素;裂缝网络渗透率越高、人工主裂缝越长、人工主裂缝渗透率越高,初期产气量越高;而页岩气吸附解吸对初期产气量的影响不明显;考虑毛管力的作用,压裂液返排率越低,产气量反而越高,这与现场实际生产情况相符合。
符号解释:
Km——页岩基质表观渗透率,mD;Km0——页岩基质绝对渗透率,mD;μg——气体黏度,mPa⋅s;DK——克努森扩散系数,mm2/s;p——气体压力,MPa;a——稀薄系数;b——滑脱系数;r——孔隙半径,mm;R——通用气体常数,J/(kmol⋅K),取值为8 314;T ——储层温度,K;Mg——气体摩尔质量,kg/kmol;β——转换系数,取值为10-6;Bg——气体的体积系数,m3/m3;pmg——基质中气相的压力,MPa;t——时间,s;φm——基质孔隙度;ρs——页岩基质密度,kg/m3;VL——朗格缪尔体积,m3/kg;pL——朗格缪尔压力,MPa;Kf——裂缝网络的渗透率,mD;Kfrg——裂缝网络中气相的相对渗透率;pfg——裂缝网络中气相的压力,MPa;α——窜流系数,m-2;φf——裂缝网络的孔隙度;Sfw——裂缝网络的含水饱和度;Kfrw——裂缝网络中水相的相对渗透率;μw——压裂液黏度,mPa⋅s;Bw——压裂液体积系数,m3/m3;pfcw——裂缝网络中的毛管力,MPa;Kf0——裂缝网络的初始渗透率,mD;βf——应力敏感系数;pi——原始地层压力,MPa;KF——人工主裂缝的渗透率,mD;KFrg——人工主裂缝中气相的相对渗透率;pFg——人工主裂缝中气相的压力,MPa;qsg——地面标准状况下的产气量,m3/s;φF——人工主裂缝的孔隙度;SFw——人工主裂缝的含水饱和度;KFrw——人工主裂缝中水相的相对渗透率;pFcw——人工主裂缝中的毛管力,MPa;qsw——地面标准状况下的产水量,m3/s;Krg——裂缝网络和人工主裂缝中的气相相对渗透率;Krg0——在束缚水饱和度条件下裂缝网络和人工主裂缝中的气相相对渗透率;Swe——裂缝网络和人工主裂缝中的有效含水饱和度;λ——经验常数,取值为2;Krw——裂缝网络和人工主裂缝中的水相相对渗透率;Krw0——在束缚水饱和度条件下裂缝网络和人工主裂缝中的水相相对渗透率;Swr——裂缝网络和人工主裂缝中的束缚水饱和度;Sgr——裂缝网络和人工主裂缝中的束缚气饱和度;σ——气-水两相界面张力,dyn/cm;a1,a2,a3——经验常数,取值分别为1.86,6.42,0.5;LF——人工主裂缝长度,m。

