辫状河内部构型递进式建模方法

姚舒萍， 李少华， 王 军， 陈德坡， 于金彪， 史敬华

(1.长江大学 地球科学学院，武汉 430100;2.中石化胜利油田研究院，东营 257000)

0 引言

近些年，河流相储层构型分析已成为老油田精细油藏描述的关键技术之一[1]。自著名河流学专家Miall[2]提出储层构型的概念及研究方法以来，国内、外学者对储层构型做了大量的探索性工作，尤其在曲流河砂体方面取得了丰富的研究成果。目前辫状河砂体储层内部构型数据资料，主要来源于现代沉积及野外露头资料，在构型模式、定量关系以及地下储层构型表征方法方面取得了一些成果和认识，但大都停留在辫流带级次[3-5]。由于存在技术、资料上的限制，对于心滩级次及其内部夹层级次的定量表征，特别是三维模型建立方面仍处于探索阶段。

张春雷[6]利用一种新的河道模型条件化算法，对河流分汊、交汇等现象进行描述和模拟，将其应用于辫状河构型建模中；白振强[7]应用基于目标的算法建立了辫状河砂体内部构型模型及参数模型；郭智[8]以建立的训练图像为依据，通过多点地质统计学的方法建立辫状河三维岩石相模型，表征辫状水道与心滩级次的相互关系；刘钰铭[9]采用序贯指示模拟与人机结合后处理的方法进行心滩内部夹层模拟。基于此，笔者提出了一种新的基于目标逐层模拟的辫状河储层构型建模方法，该方法能够较好地刻画辫状河内部构型单元的几何形态、空间分布及其相互之间的关系，得到的模型比较符合已有的地质认识。

1 原理与方法

基于目标的随机模拟方法是以目标对象为基本模拟单元，能够较好地再现模拟对象的几何形态，一般分为布尔模拟方法和Fluvsim方法[10]。

1)布尔模拟方法是基于目标的随机模拟方法中最简单的一种方法。设u为坐标随机变量，Xk是表征第k类几何物体几何形态(形态、大小和方向)的参数随机变量。第k类几何物体中心点的分布构成一点过程u，它可以用形状随机过程Xk和表示第k类几何物体出现与否的指标随机过程Ik两者的联合分布“示性”，从而构成一示性点过程。其中，

(1)

布尔模拟方法实现的一般步骤为：①随机抽样产生预测砂体中心位置(x,z)；②判断是否与已知井位处的数据发生冲突，是则调整该砂体，使之不冲突，否则进行下一步；③从经验累积概率分布函数中随机抽取该砂体厚度；④由已确定的厚度—宽度关系确定砂体宽度；⑤计算目标函数值(Fs)为式(2)；

Fs= 砂体剖面面积/剖面总面积

(2)

⑥转到步骤②产生另一个砂体，计算Fs值，直至达到给定阙值为止。

2)Fluvsim算法是由Deutsch[12]设计的用于复杂河道建模的模拟方法，一般用于曲流河和冲积扇中的辫流水道建模。在该方法中，Deutsch认为储层是一个层次系统，因而其建模是在层次分析的基础上分层次逐级建模。Fluvsim方法具有以下特点：①具有一个清晰可逆的层次坐标系统；②地质上的直观认识和输入参数控制着河道的大小和形状；③对垂向上和实际的岩相比例差异进行明显的控制；④真实的不对称的河道几何形态；⑤真实的无波状河道顶面[11]。

现有的两种基于目标的方法中，布尔模拟方法只能针对单一目标体的几何形态进行模拟，无法建立起多个目标体之间的联系。Fluvsim方法则是专门针对曲流河建模的一种算法，无法直接用于辫状河模型，而且难于条件化，特别在当需要条件化的资料较多时[10]。由此可见，仅仅使用单一的基于目标的方法无法满足辫状河内部构型单元的模型建立。因此，需要在基于目标的方法基础之上，结合其他手段(商业化建模软件Petrel)和策略，使之能够适用于辫状河储层模型。

基于目标的方法在商业化建模软件Petrel中通常分为2个模块：①采用Fluvsim算法的河道模拟模块；②采用布尔模拟的预设模块。

在河道模拟模块中，可进一步细分为5个部分：①Setting选项可对河道进行重命名、设置河道的体积百分比、河道数量、天然堤是否侵蚀先期河道以及河道能否穿过地层的顶底面；②Layout选项可从平面上设置河道的方向、振幅和波长；③Channel选项可从剖面上设置河道的宽度和厚度；④Levee选项可对天然堤的宽度和厚度进行设置(由于辫状河中不存在天然堤微相，因此不勾选此选项)；⑤Trends选项可选择多种趋势(平面趋势、垂向趋势、流线和点源)来约束河道的发育。

在预设模块中，可进一步细分为4个部分：①Setting选项可对目标体进行重命名、设置目标体的体积百分比、目标体数量以及目标体在体模型内是否完整；②Geometry选项可设置目标体的几何形态(有箱形、管状、椭圆等数十种几何形态，若选择椭圆则还需设置剖面几何形态——锐边等四种，若选择其他则不需要)、主方向、宽度、长宽比及厚度，其中厚度还可通过与宽度的比值来确定；③Trend选项可选择多种趋势(垂向趋势、平面趋势、体积趋势和流线)来约束目标体的发育；④Rules选项可设置替换规则以及目标体的完整与独立。根据上述说明只能生成单一的目标体，无法满足已有的辫状河构型模式。

因此，在基于目标的方法基础之上，采用递进式的建模策略，依次逐层生成复合河道、心滩和落淤层，通过设置相关参数和规则建立起多个构型单元之间的联系，从而实现辫状河内部构型建模。这种递进式的建模方法基本思路为：①运用商业化建模软件Petrel建立工区的三维网格模型，由于心滩内部落淤层通常较薄，因此垂向上的网格需要足够精细；②采用基于目标的方法中河道模拟模块生成复合河道，设置河道体积百分比、方向、振幅、波长、宽度和厚度，为了保证河道的完整性，将其限制在工区内部。接下来选择预设模块中的椭圆和底平顶凸的几何形态，设置心滩体积占整个工区的百分比、方向、宽度、长宽比和厚度在河道内部模拟心滩；③仍然应用预设模块中的椭圆和锐边，设置落淤层体积占整个工区的百分比、方向、宽度、长宽比和厚度在心滩内部模拟落淤层。

2 理论模型的建立

假设X工区长约1 000 m，宽约1 000 m，厚约30 m。首先建立储层构造格架模型，以20 m×20 m×0.1 m为单一网格精度，采用等比例的方法进行网格划分，则网格总数为50×50×300=7.5×105个。然后按一定的相比例在砂体单元骨架内采用基于目标的建模方法建立构型单元模型，根据递进式的建模策略依次生成符合辫状河构型模式的复合河道、心滩和落淤层。

基于目标的建模方法的重点就是将各类构型单元的几何形态参数化。将复合河道、心滩和落淤层作为Fluvsim方法的目标体，分别给每个目标体进行编码：背景相(代码0)、河道(代码1)、心滩(代码2)和落淤层(代码3)。每个目标体的百分比是指该目标体体积占整个工区的百分比，可以通过垂直比例曲线、区域比例图及参考全局比例来确定，而这三种类型的比例可以通过井和地震数据的结合获得。假设复合河道、心滩和落淤层的体积占整个工区的百分比分别为：30%、20%、1%。

2.1 复合河道模型

2.1.1 相关参数的设置

复合河道是由不同位置、不同期次的单一河道相互叠置、切割形成的。为了使模型更符合辫状河地质模式，只需要建立河道模型并将其限定在一定范围内即可。每条河道的几何形态由方向、振幅、波长、宽度和厚度确定(图1)，并通过三角分布设定每个参数的取值范围。三角分布可设定最小值a、最可能的值b和最大值c，一个数接近a和c的概率均小于接近b的概率。这种方法既能控制参数的范围，又能一定程度上合理的反映概率的大小，根据数据统计来设定参数，可降低河道模拟的不确定性。生成模型时，参数的设置允许有一定的偏差，偏差越大则河道的活动性越强，通常用分数表示。若偏差为0.1，则参数的变化范围为数值的±10%。由于数据统计和随机模拟均具有一定的不确定性，故偏差不能全部为“0”。与曲流河不同的是，辫状河表现为低弯度、多河道、宽而浅的特征，总体起伏不大，即偏差很小。

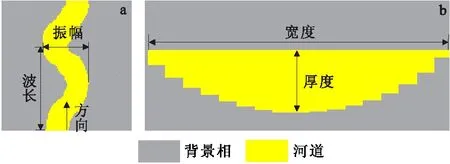
图1 河道几何形态的参数示意图Fig.1 The parameter type of the channel geometry(a)平面示意图;(b)剖面示意图

图2 复合河道的三维模型Fig.2 The 3D model of the combination channel(a)河道不受任何限制;(b)河道受到约束

在平面上，河道的平均方位角控制着主方向往两侧偏移的幅度。振幅控制着河道在平面上弯曲的程度，振幅越大则河流越弯曲，本次建模对象为辫状河而非曲流河，因此振幅可适当平稳。波长控制着一个周期内河道的延伸长度，波长越长则河道的延伸长度就越长。在剖面上，河道呈顶平底凸的几何形态。河道宽度和厚度同时控制着河道在剖面上的几何形态。参考国内、外专家对砂质辫状河的研究分析得到河道的宽厚比，发现河道的厚度和宽度具有一定的相关性，因此在已知宽度的情况下，可通过两者之间的经验公式来控制河道厚度，从而约束河道的剖面几何形态，同时要保证河道只能发育在工区内部。

2.1.2 模型的建立

参考辫状河内部构型相关文献，搜集不同尺度、不同规模、不同区域辫状河道的相关数据，经过整理并分析得到经验数据和经验公式，可用于设置河道的相关参数。得到的结果只是理论模型，若有实际工区资料，则根据工区内搜集的数据进行参数设置。经过现代地质调查可知，活动河道的宽度一般为120 m～380 m，平均宽度约为220 m[12]。河道砂体的厚度为3 m～10 m，平均宽厚比为40～100[13]。

已知河道体积占工区的30%，平面上河道主方向约为0°，振幅为10 m～30 m，以20 m居多；波长为400 m～500 m，以450 m居多。剖面上河道宽度为68 m～260 m，以180 m居多；厚度为3 m～5 m，以4.8 m居多。分别模拟两种情况：①河道不受任何限制(图2(a))；②河道受到约束(图2(b))。

图2为模拟的两种三维模型，当河道受到约束时，更符合辫状河地质模式，即图2(b)满足。

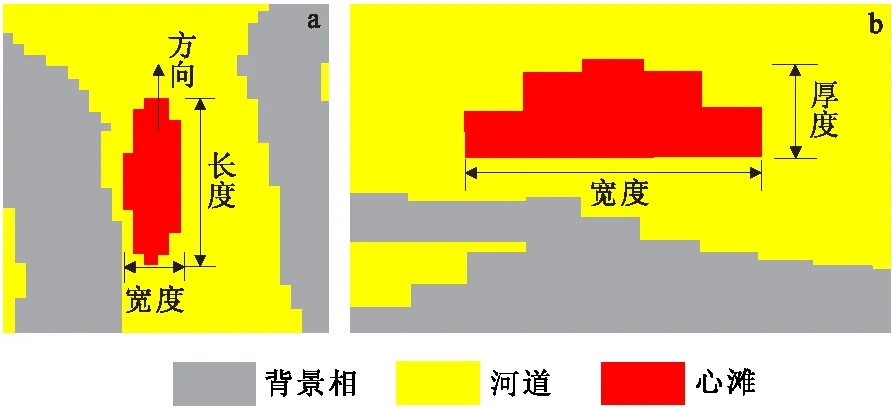
图3 心滩几何形态的参数示意图Fig.3 The parameter type of the bar geometry(a)平面示意图;(b)剖面示意图

2.2 心滩模型

2.2.1 相关参数的设置

每个心滩的几何形态由方向、宽度、长宽比和厚度确定(图3)，进一步通过三角分布设定每个参数的取值范围，使心滩的模拟更合理化。在平面上，由于心滩的几何形态与椭圆相近，因此将其平面形态定义为椭圆，通过改变长短轴的相关参数控制心滩的平面形态。心滩主轴方向不同会形成不同的心滩，在辫状河中心滩有三种类型：①斜向心滩；②横向心滩；③纵向心滩，它们沿着不同的方向分布在河道不同的位置。心滩宽度类似于椭圆的短轴，心滩长宽比是指椭圆长轴与短轴的比值。经过野外露头和现代沉积统计分析发现心滩的长宽比具有一定的相关性，它们之间的比值可通过经验公式得到。在剖面上，心滩呈底平顶凸的几何形态，通过改变厚度与宽度来控制心滩的剖面形态。除了心滩的长宽比具有一定的相关性，其宽厚比的相关性也很强，因此在已知宽度的情况下，厚度有时也可用两者之间的经验公式来表示。

2.2.2 模型的建立

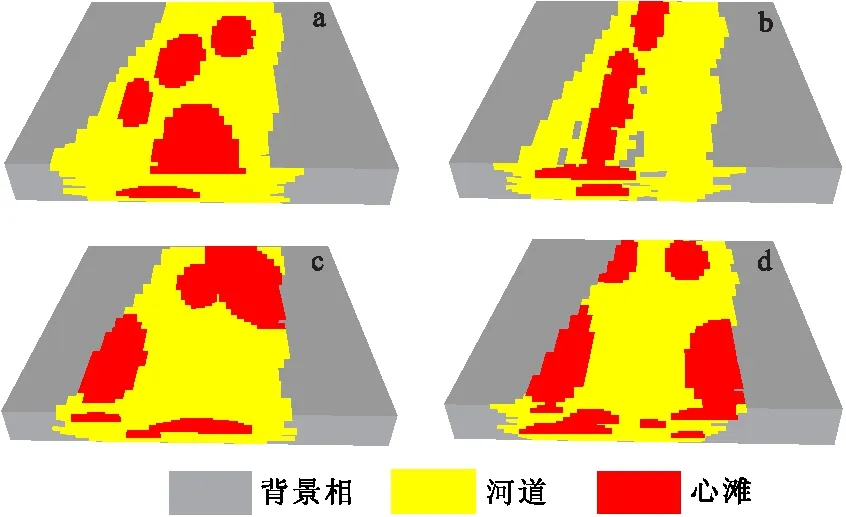
图4 包含心滩的三维模型Fig.4 The 3D model of the bar(a)有完整性和独立性；(b)有完整性无独立性；(c)无完整性和独立性；(d)无完整性有独立性

图5 落淤层形态的参数示意图Fig.5 The parameter type of the interlayer geometry(a)平面示意图;(b)剖面示意图

根据辫状河构型模式，心滩一般发育在河道内部，因此在设置心滩分布的规则时，应将其设为只能替代河道(目标体1)。本次模拟假定心滩体积占整个工区的20%，平面上心滩主方向为-20°～20°，以0°居多；宽度为128 m～300 m，以280 m居多；长宽比为2～3，以2.3居多。剖面上心滩厚度为4 m～10 m，以9 m居多。输入同样的参数，只改变心滩的完整性和独立性，分别模拟四种情况进行分析，如图4(a)～图4(d)所示。

图4代表心滩不同分布规则的四种情况，根据辫状河构型模式，只有图4a满足，即心滩具有完整性和独立性。

2.3 落淤层模型

2.3.1 相关参数的设置

落淤层是当洪水能量衰减时，细粒悬浮物质在心滩上垂向加积形成，发育在心滩内部增生体之间，受心滩规模的约束。因此落淤层的平面几何形态与心滩类似，故将其平面几何形态定义为椭圆形，由方向、宽度、长宽比来确定(图5)。与心滩不同的是，根据落淤层的形成机理，在剖面上其厚度很薄且形态有2种：①近水平式；②穹隆式[4]，因此选择锐边来刻画落淤层的剖面几何形态。

2.3.2 模型的建立

根据落淤层的形成机理，其在平面上的展布形态与心滩类似，因此具有和心滩相近的长宽比，但是由于后期沉积环境和水动力条件的变化，导致其规模大小各异。在大庆油田萨中密井网区通过丰富的钻井资料对进行古辫状河心滩内部夹层的研究，发现落淤层大部分位于心滩的后部，其长度为150 m～400 m，平均为300 m；宽度为50 m～180 m，平均125 m；厚度为0.1 m～0.4 m，平均为0.25 m；其长轴方向与心滩长轴方向基本一致，夹角小于20°，多为0°～10°[15]。

根据辫状河构型模式，落淤层为心滩内部的构型单元，因此在设置规则时应将其定义为只替代心滩部分(目标体2)。本次模拟假定落淤层占整个工区的1%，平面上落淤层的主方向为0°～20°，以0°～10°居多；宽度为50 m～180 m，以125 m居多；长宽比为2～3，以2.5居多。剖面上落淤层厚度为0.1 m～0.4 m，以0.25 m居多。输入相同的参数，只改变落淤层的完整性和独立性，分别模拟四种情况进行分析，如图6(a)～图6(d)所示。

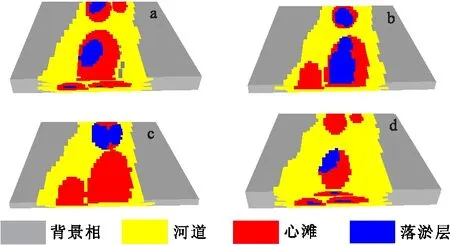
图6 包含落淤层的三维模型Fig.6 The 3D model of the interlayer(a)有完整性和独立性；(b)有完整性无独立性；(c)无完整性和独立性；(d)无完整性有独立性

图6代表落淤层不同分布规则的四种情况，根据辫状河构型模式，只有图6(a)满足，即落淤层具有完整性和独立性。

3 结论

1)在基于目标的方法基础之上，采用递进式的建模策略，能够对构型单元的几何形态、空间分布和相互之间的关系进行合理刻画。首先模拟复合河道，其几何形态由方向、振幅、波长、宽度和厚度确定，且被限制在一定范围内；由于心滩一般发育在河道内部，然后在河道内部模拟心滩，其几何形态均由方向、宽度、长宽比和厚度确定；而落淤层则一般发育在心滩内部，接下来则在心滩内部模拟落淤层，其几何形态也由方向、宽度、长宽比和厚度确定。为了符合已有的辫状河地质认识，须保证心滩和落淤层的完整性和独立性。

2)这种递进式的建模方法能一定程度上精细地刻画目标体的几何形态、空间分布及其相互之间的联系，但仍然具有某些的局限性。例如只能保证心滩出现在河道内部，却无法确保剖面上心滩底部与河道底部之间仍然充填心滩；只能控制心滩内部落淤层的体积百分比，无法定量化表征落淤层的数量及其相互之间的间距；落淤层在剖面上近水平式或穹窿式的几何形态，只能选择预设模块中的椭圆才能够进一步选择剖面上的预设模块——锐边，没有合适的模块完美刻画其几何形态。因此，需要探索新的方法进行更合理化的建模。