基于SVD和PCA方法重构干涉格林函数

张 俊， 熊章强，2， 张大洲，2， 陈 杰， 刘云昌

(1.中南大学 地球科学与信息物理学院，长沙 410083；2.中南大学 有色金属成矿预测教育部重点实验室，长沙 410083)

0 前言

地震干涉法[1](Seismic Interferometry，SI)被用来计算两个接收点之间的近似格林函数，其基本假设是其中一个点作为虚拟源，计算空间内不同源点下两接收点之间记录的互相关，然后将不同源点的互相关结果叠加就可得到标准的干涉格林函数。上述所涉及到的源可以是人工源[2]、天然地震源[3]、随机噪声源[4-6]等。由于地震干涉法的部分震源所产生的地震波在传播过程中会相互干涉产生伪影，从而影响计算得到的格林函数的准确性。因此，计算出一个更加准确的格林函数对于地震勘探，尤其是微动勘探的数据处理就显得非常重要。

通常为了得到两个接收点之间准确的格林函数，一般要求检波器接收到来自一个封闭曲面内的震源，震源类型包括单极子和偶极子源。自2004年以来，Snieder、Weaver、Wapenaar等[4，7-10]的研究结果表明：两个接收点之间所计算的格林函数仅由部分震源所产生的地震波来获得。对于在菲涅尔带内震源采用固定相方法做近似积分计算格林函数可以得到较好的结果。而处于菲涅耳带外的震源则会产生快速发散的能量从而破坏干涉能量。对于整个区域而言，震源在覆盖不完整或者没有偶极子源的情况下，恢复得到的格林函数质量就相对较差。然而在实际的工作中，很少使用偶极子源，源分布通常也是不完整的。因此，目前在提高格林函数质量时，重点在于地震波传播时所到达的时间(延时)，而不是恢复传播过程中的真实振幅。

为了提高干涉格林函数计算的准确度，解决源覆盖不完整的问题，Gabriela Melo等[10]使用奇异值分解方法对叠前互相关谱进行分解，重构一个秩为“1”的矩阵后计算得到近似格林函数，解决某些情况下震源不完整覆盖下的问题，取得了较好的效果。笔者使用奇异值分解[10-12](Singular Value Decomposition，SVD)并结合主成分分析[13-15](principal component analysis，PCA)两种方法计算近似格林函数，通过理论分析、数值模拟以及实测数据处理，分析对比格林函数在计算过程中部分源产生干扰影响，使用两种方法结合来压制干扰、提高格林函数计算的准确性。

1 地震干涉理论与算法

1.1 地震干涉法(SI)

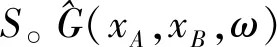
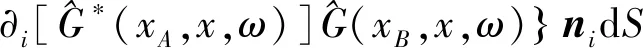
(1)

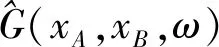
式(1)中包含两点间所有单极子源和偶极子源的互相关。为了简化处理流程，首先在积分运算中减少一个互相关因子，其次只考虑单极子源。假设介质是均匀的(速度c和密度ρ为常量)，其外部边界为S，且没有来自边界外部的能量，则方程简化为式(2)

(2)

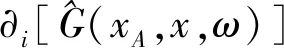
(3)

式中α(x)是x和法向量在边界S射线之间的角度。假设S足够大，则有α(x)≈0和cos[α(x)]≈1，则公式(2)可简化为式(4)。

(4)

由于在公式推导过程中做了相应的简化，使计算得到的格林函数丢失了真实振幅，但相位没有损失，且式(4)适用于大多数地震干涉。为了提高地震波旅行时间的准确度，边界从连续到离散情况下，忽略方程(4)的振幅因子2/ρc。因此干涉格林函数可以写成各源得到的互关联之和

(5)

式中M是源的数量。

设xi(1≤i≤M)为源位置，τ为时间域的互相关滞后时间。根据SI在频率域的推导方程，可以由它写出时间域的方程。因此，互相关函数C可以写成：

(6)

其中C(xi,τ)为在源xi的作用下xA和xB求得的互相关。A、B两点间的格林函数G为各源的互相关之和，则有

G=G(xB,xA,t)+G(xB,xA,-t)=

(7)

1.2 奇异值分解(SVD)

G=G(xB,xA,t)+G(xB,xA,-t)=eC

(8)

式中：e为m个全为1的列向量；C为m个长度为2n-1的行向量，它的每一行表示各源传播到两点接收记录的互相关，各源的互相关记录构成如图1所示的互相关谱。

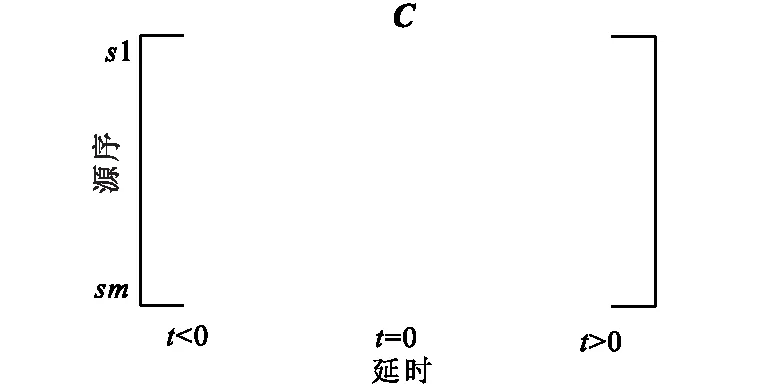
图1 两点间源的互相关谱Fig.1 The cross-correlogram for sources

由奇异值分解法，则式(8)的格林函数可以写成：

G=e1×mCm×(2n-1)=

(9)

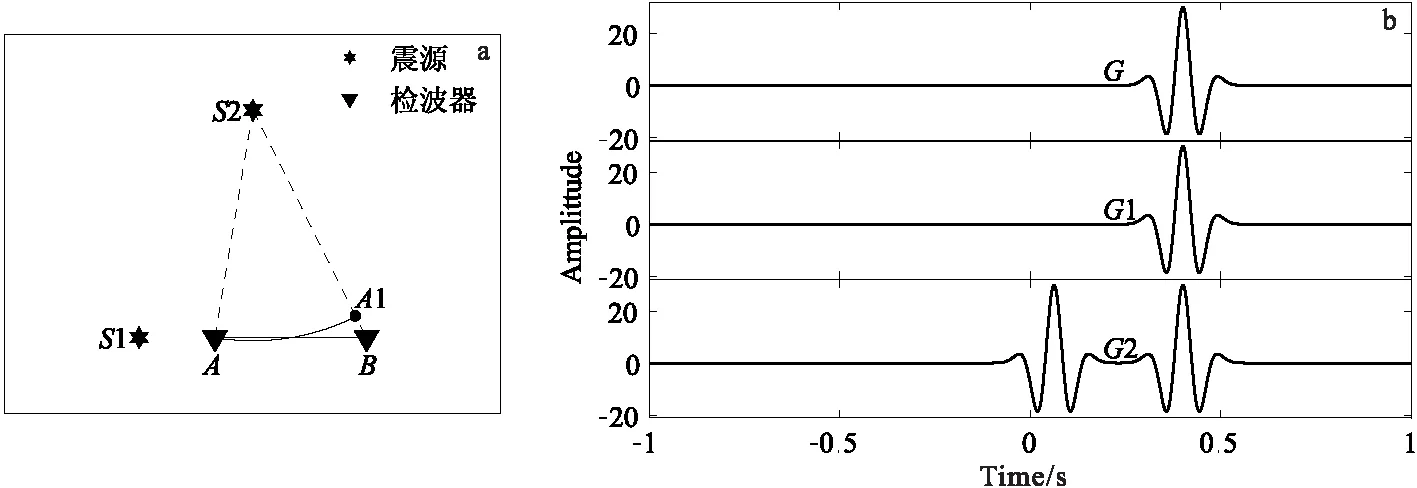
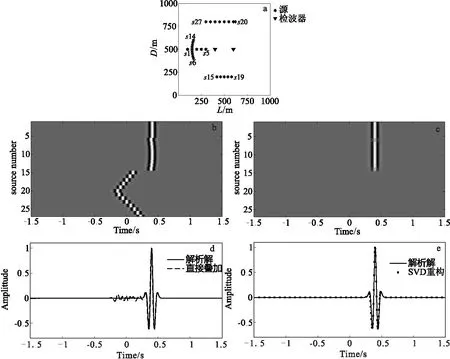
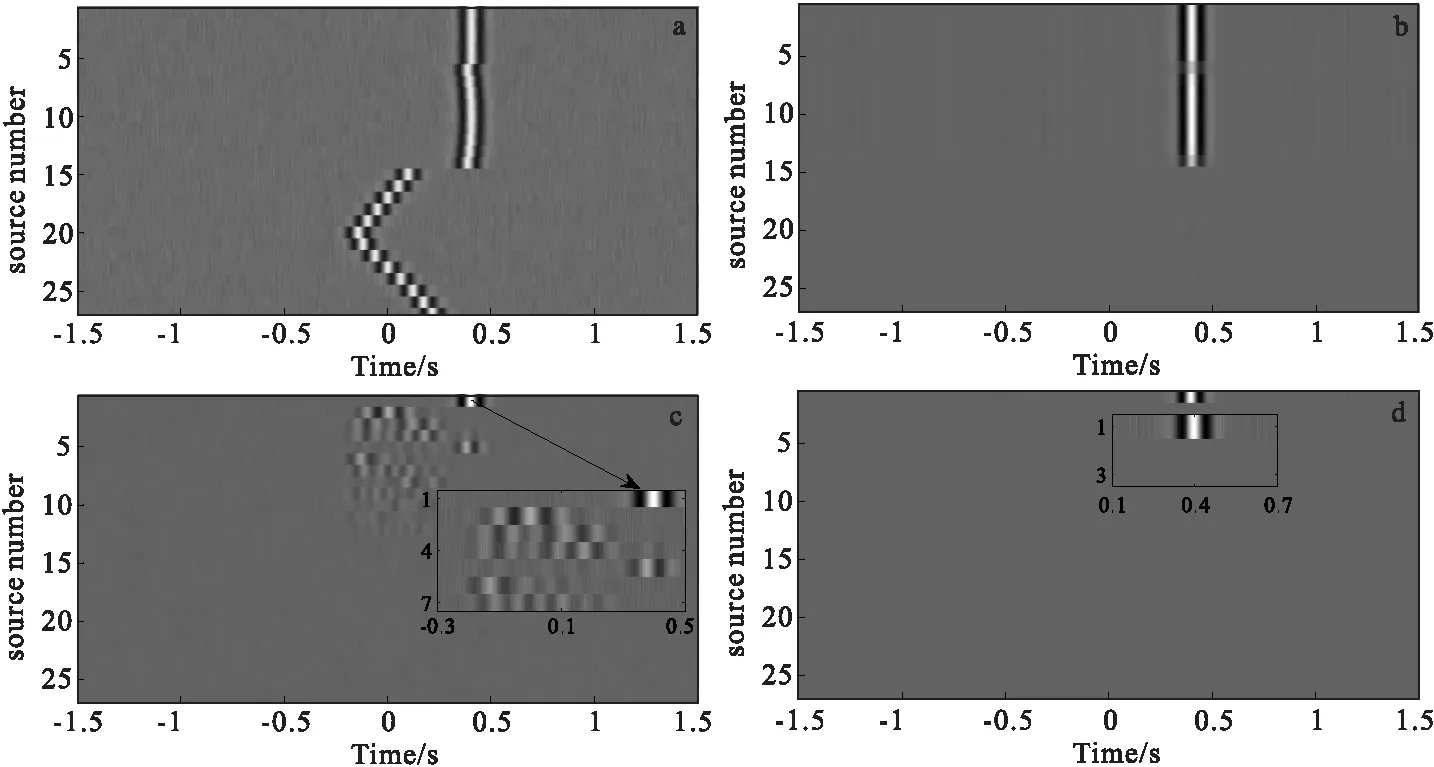
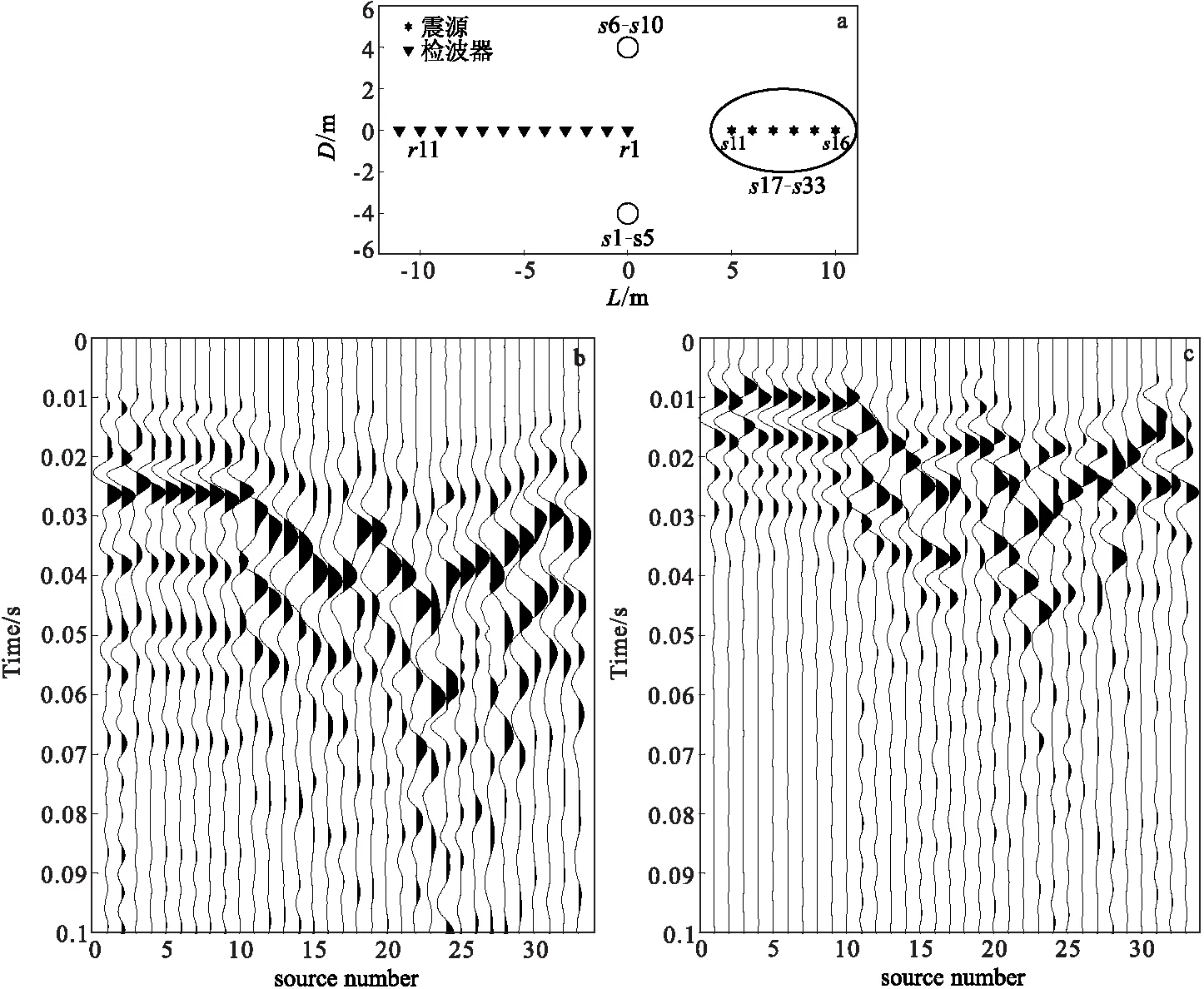
式中：T为转置;s=eUS为右奇异值向量V的权系数，称之为叠加系数。而当sk=0,M

(10)

将求得的sk按绝对值大小排序，求贡献率Qj为式(11)。

(11)

在找出一个适合的贡献率Qj后就可以得到j，然后根据一个低秩的矩阵近似等于原矩阵的概念，保持S的前j个奇异值Sj重构得到一个低秩的近似矩阵。则重构的干涉格林函数为式(12)。

1≤k≤j

(12)

1.3 主成分分析(PCA)

主成分分析(PCA)是一种分析、简化数据集的方法，可以用来降低数据集的维数，同时保持数据集中的对方差贡献最大的特征[14-15]。对重构的低秩互相关谱Cj降维计算新的格林函数，假设一个矩阵为X，维度为m，各维度下具有n个样本数。将X进行线性变换变成另一个矩阵Y，使得Y的协方差矩阵为对角矩阵。Y是对原始矩阵X提取主成分后的协方差矩阵，用它可以对原始矩阵X分析主成分构造并实现降维处理。对于矩阵X，其矩阵大小为m×n，则X可写成式(13)。

(13)

根据主成分分析的理论[13]，首先对X进行均一化

(14)

(15)

2 实验结果与分析

2.1 有效震源分析

如图2(a)所示，在一均匀各向同性介质的区域内，位于A、B两点设置两个检波器，在S1、S2两点设置两个震源。第一类源S1位于AB直线任意位置但非AB内(文中设置在A左侧)，第二类源S2位于AB连线两侧。当仅有第一类源S1时，计算得到的近似格林函数G1与真实格林函数G一致，如图2(b)中的G和G1曲线所示，峰值时间刚好为源由A传至B的旅行时差(延时)。当源S1和S2同时存在时，计算得到的近似格林函数如图2(b)中G2所示，可以看出G2与真实格林函数G有所不同。根据干涉原理可知，当在S2点激发的地震波被A、B两个检波器接收后进行互相关计算，其实质是在S2和B点连线上的虚拟接收点A’所接收到的信号的互相关，此处点S2到点A的距离和点S2到点A’的距离相等。通过以上分析可知，当震源位于两个接收点连线的两侧时，计算得到的格林函数不是严格意义上接收点A和B之间的干涉格林函数，而且这个计算得到的干涉格林函数中信号的到达时间比真实的时间要小，也就是在计算得到的格林函数中在准确格林函数之前还存在一个信号。这主要是因为虚拟接收点A’到B点的距离较A点到B的距离较小引起的。

图2 不同震源位置计算得到的格林函数对比Fig.2 Compare and analyze the green function(a)观测系统图;(b)格林函数对比图

图3 合成数据处理结果Fig.3 Synthesized data processing results(a)观测系统；(b)原始互相关谱；(c)解析解与直接叠加对比;(d)SVD重构互相关谱；(e)解析解与SVD重构解对

通过对不同位置震源的近似格林函数峰值延时进行分析发现，第一类源计算得到的峰值延时最大，与真实格林函数的峰值时间一致。对于格林函数GAB，源在接收点A、B中线左侧的峰值为正延时，反之为负延时。在各向同性均匀介质中第二类源计算结果会对格林函数产生不同程度的影响，其中靠近AB延长线两侧(双曲线范围内)的影响较小，它们的峰值延时也必定位于真实格林函数峰值时间的正负值之间，这将会引起计算得到的近似格林函数的峰值延时减小，而对于实测数据的处理，选择一个参考具有重要的意义。

2.2 数值模拟及数据处理

在实测的地震数据处理应用中，台站接收到的信号来自各个方向，台站连线两侧的振动信号将影响计算真实格林函数，因此采用SVD和PCA对重构更加准确的格林函数具有重要作用。我们使用数值模拟方法，对来自不同方向的地震记录进行处理，再使用PCA的方法分离出主信号(主信号)，求取得到新的格林函数。由于传统标准格林函数计算中采用直接叠加互相关的方法得到的格林函数与真实格林函数有差别，其主要影响来自连线两侧的震源，在使用SVD分解时可以对其起到很好地压制作用。如图3(a)所示，在一个1 000 m×1 000 m的均匀各向同性空间区域内不同位置处布置震源，其中在接收点A、B连线左侧布置14个震源，横向两侧分别布置5个和8个震源，共27个源。

图4 加噪后重构互相关谱对比Fig.4 Reconstructed correlogram with noise(a)原始互相关谱;(b)SVD重构互相关谱;(c)PCA重构互相关谱;(d)SVD+PCA重构互相关谱

由图3(b)和图3(d)可知，SVD重构得到的低秩互相关谱，较好地压制了来自远离A、B连线方向震源(S15-S27)的能量，保留来自纵向及其附近震源的能量(S1-S14)。这说明在纵向附近的源对格林函数的影响较小。结合图3(c)和3(e)可以看出，远离纵向的这部分能量影响了真实格林函数，在SVD方法处理后，影响格林函数的能量被很好地压制。因此，更加确定来自A、B两点间纵向的源对格林函数产生积极作用。

为了验证在有噪声的情况下，PCA能够更好地分离出有效信号。对上面相同情况下模拟的信号添加白噪声，然后进行处理分析(图4)。这里以信噪比为标准进行定量对比分析，定义信噪比为：

(16)

式中：S为有效信号；SN为加噪信号。

从图4中可以看出，SVD对于压制侧向能量的影响效果明显，而PCA对于提取主信号具有很好的效果。因此在SVD处理后互相关谱具有很好的同相轴性质，再使用PCA进行提取同相轴的互相关谱，能够快速分离得到有效的格林函数，其互相关谱如图4(d)所示。此外，还使用上述公式计算加噪后各处理方法得到格林函数与真实格林函数的性噪比，SVD处理后的性噪比为22.3 dB，PCA处理后的性噪比为18.5 dB，SVD和PCA同时处理后的性噪比为36.3 dB。

2.3 实测数据处理

为了验证上述理论分析及模拟结果的准确性，在某处地形平坦区域使用锤击作为震源，在不同位置进行激发并采集数据，观测系统如图5所示。源s1～s10分布位于r1左右两侧4 m处的小圆内；源s11～s16位于排列纵向右侧，距离r1最近的s11有5 m，随后每隔1 m激发一次；源s17～s33随机位于排列左侧横向两侧(椭圆内)。检波器共有12道，道间距为1 m，总共采集了33个不同位置源点的数据。图5(b)和图5(c)为1号检波器和11号检波器在不同震源激发下接收到的波形记录，图中可见不同位置激发的地震波先到达1号检波器，然后才到达11号检波器。

根据前面的分析可知，实测数据处理可以使用s11～s16中任意一个源的计算结果作为参考(选择s11震源数据计算格林函数作为参考)，用r1和r11接收点的波形记录计算近似干涉格林函数。在计算格林函数时先求得两点间的互相关谱。图6(a)、图6(b)和图6(c)分别为直接叠加、SVD及SVD+PCA结合处理后的互相关谱，图6(d)为不同方法计算近似干涉格林函数进行对比分析。

图5 两接收器波形记录图Fig.5 The waveform of two receivers(a)数据采集布置; (b)r1记录; (c)r11记录

图6 两道实测数据处理结果Fig.6 Field data processing results(a)原始互相关谱;(b)SVD重构互相关谱;(c)SVD+PCA重构互相关谱;(d)四种格林函数对比

从图6(a)原始互相关谱可以看出，s11峰值时间、最大时间轴以及能量集中区域均在0.022 s附近，而s1～s10峰值位于0.01 s附近产生了较强的同相轴。在经过图6(b)的SVD分解后，椭圆内的部分源被不同程度的压制，但是s1～s10的同相轴仍然清晰可见。经过对SVD重构的低秩互相关谱采用PCA方法分离主信号得到图6(c)所示的结果，然后在计算新的格林函数。图6(d)为不同方法求得的格林函数对比图，由图6(d)中可知，直接叠加法将0.01 s附近的干扰加到了格林函数中，引起了0.005 s处相位改变以及0.018 s处的峰值时间右移减小。在使用SVD和PCA结合处理后，上述两个位置的影响均得到了显著改善，使得计算的格林函数更加接近真实情况。

3 结论

通过计算分析不同位置的震源对格林函数的影响以及进行数值模拟与实测数据资料处理，得出如下结论：

1)在均匀各向同性介质中，两个接收点连线方向上的震源对格林函数起主要作用，而两个接收点横向两侧的震源对格林函数的计算结果有不同程度的影响。

2)使用SVD和PCA结合方法重构互相关谱可有效压制部分干扰震源对格林函数的影响，而分离提取格林函数的主要成分，可有效提高计算近似格林函数的准确性。