动基座下自调平台对方位角测量的影响分析

李永刚 周玉堂 张忠武 王 震 赵功伟

(北京航天计量测试技术研究所，北京 100076)

1 引 言

经纬仪类仪器以大地水平面作为工作基准，在动基座条件下，没有能保持水平的稳定基准面，使经纬仪类仪器难以应用于动基座条件，使动基座环境下(例如船上)的角度高精度测量或传递变得难以实现。解决办法是通过研制一种自调平工作台，由自调平工作台通过传感器和执行器件自动保持台面水平，把经纬仪类仪器安装在自调平工作台的工作面上，从而使经纬仪类仪器用于动基座环境成为可能。

自调平工作台以对线加速度不敏感的光纤陀螺、提取工作台台面摆动的角速率信号，经控制电路处理后，驱动电机，使工作台台面作反向摆动，进行伺服跟踪；用装于台面上的石英摆式加速度计信号，经滤波电路后，作为校零信号，定时进行自动校零，从而保持工作台台面的动态水平度，实现自调平功能[1]。

经纬仪类仪器要求双向水平度，因此所用的自调平工作台需具有双向调平功能，即需采用双向自调平工作台。

自调平工作台用于经纬仪类仪器，保持双向动态水平度；自调平工作台从结构上可分为转台式自调平台和杠杆式自调平台两种，转台式自调平台是双轴转台结构，能适应具有较大摆动量的动基座，但承载的测量仪器的型号不能随意改动，否则自调平台的轴系平衡会被打破，从而影响调平准确度；杠杆式自调平台式工作台由滚珠丝杆的升降控制、绕单边轴系摆动，该结构形式承载能力大，对负载的变化不敏感，但容许动基座的摆动幅值较小，若需增大摆动量，又会降低对动态水平度的调节分辨力。

在传递方位角的自调平工作台绕X、Y两个轴转动，以达到两个水平方向调整到一定水平度的目的，提供水平基准。在以前的使用中认为，两个水平轴的实时旋转不会带来经纬仪底座方位角的变化，只是由于调平台的旋臂转动带来了经纬仪的线位移，这样，经纬仪在船上进行多个目标瞄准测量时，可以认为是准静态测量，即经纬仪与被测目标之间的角度关系不会发生变化。然而，后来经仿真分析和试验发现，事实并非如此。

经纬仪在进行方位角的传递时，一般是先对瞄一个目标，然后再进行另一个目标的对瞄。如图1所示，将两台经纬仪都安放在自调平台上，经纬仪Ⅰ对基准镜自准直测量，再与经纬仪Ⅱ进行对瞄测量，两次测量的夹角为α1，在进行两次对瞄之间存在一个时间差。

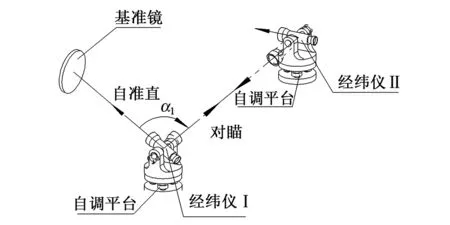
图1 使用经纬仪进行方位角传递示意图Fig.1 Azimuth angle transmission using theodolite

而在这个过程中，自调平工作台通过敏感元件敏感到船摇摆的角度，通过执行结构对水平两个方向进行实时反向调整，在调整的过程中，由于旋转轴的变化，导致了水平面相对于底座(船体)在方位上具有一定的角位移，以下将分析这种角位移的变化量。

2 自调平台调平时的坐标变换

自调平工作台的结构主要分为基座、中框、内框等三部分组成，基座随着动基座一起做运动，通过伺服控制，使内框上的工作面处于水平状态。

自调平工作台坐标系的定义，如图2所示。

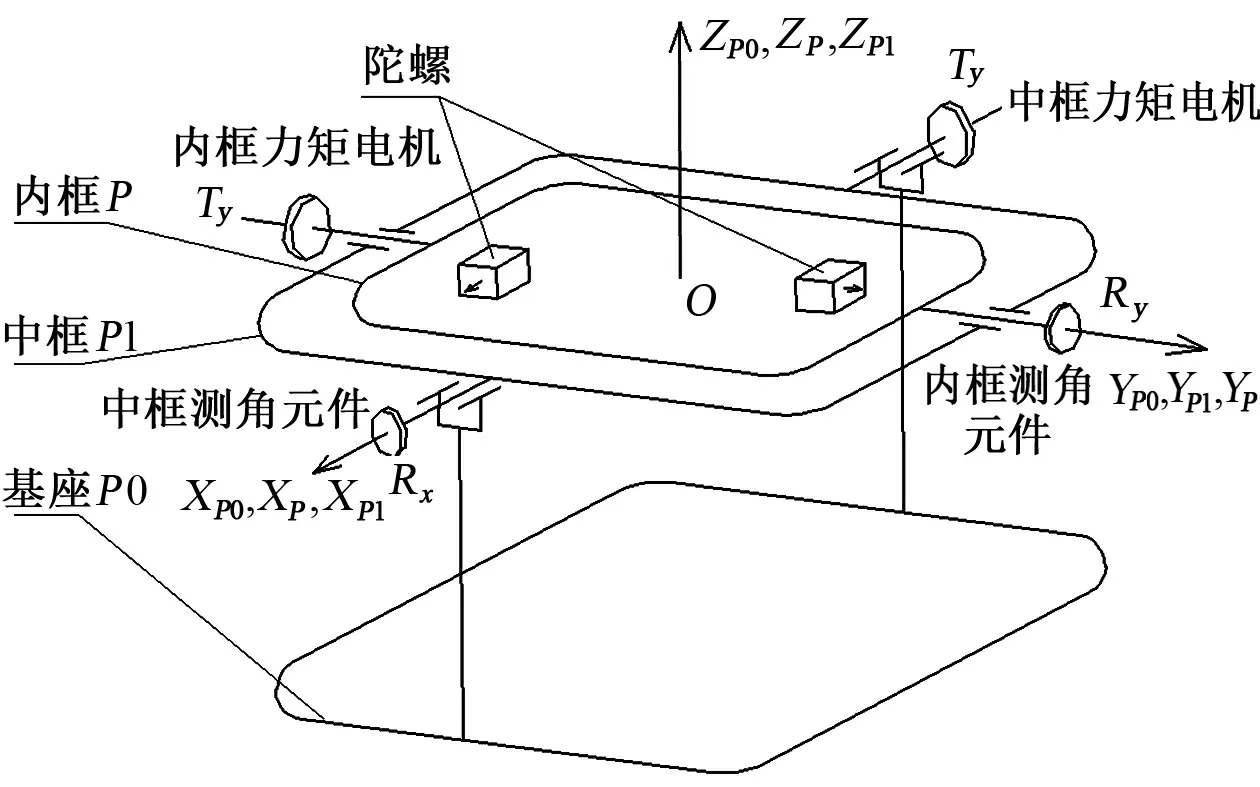
图2 自调平工作台各框轴坐标系的定义Fig.2 Coordinate system definition of self-stabilization platform shafting system

图2中，中框旋转轴系和内框旋转轴系为正交关系，P为自调平工作台内框，O为基座，与基座、中框架、内框架相固联的坐标系分别为:

OXP0YP0ZP0——与基座固联的坐标系；OXP1YP1ZP1——与中框架固联的坐标系，OXP1为中框架轴，它与基座的OXP0轴重合；OXPYPZP——与内框架固联的坐标系，OYP为内框架轴，它与中框架的OYP1轴重合。

在实际使用时，上述转台结构形式的自调平工作台具有一定的局限性，即轴系的负载需要严格平衡，对于经纬仪类的仪器来说很难实现。因此，一般是用另外一种结构形式的自调平工作台，即杠杆式自调平工作台，如图3所示，其轴系不在一个平面内，但本文只是考虑角度的转换，而角度的转换对轴系的位置并不敏感。其调平过程中，底座角度发生变化，其坐标转换关系与图2完全一致。

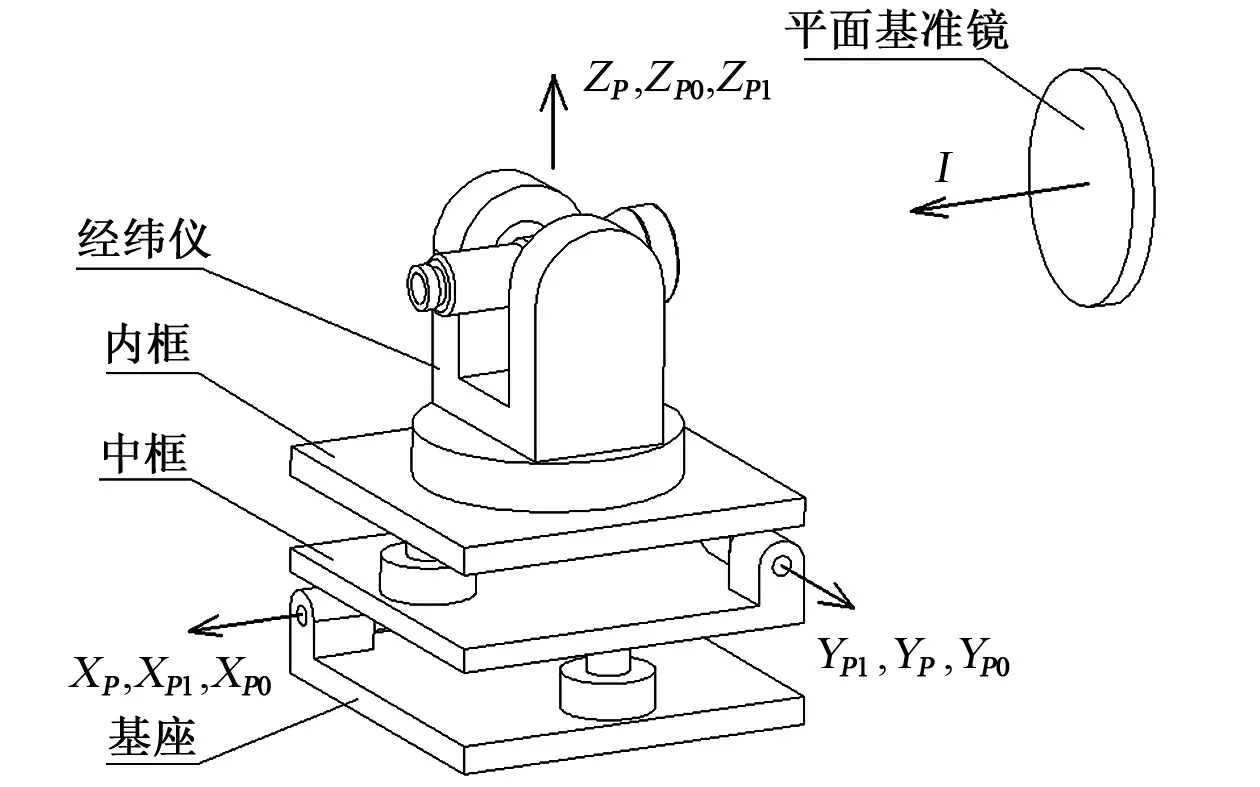
图3 杠杆式自调平台和经纬仪坐标系的定义Fig.3 Coordinate system definition of lever type self-stabilization platform and theodolite

自调平工作台调平时，各框坐标系的转换示意图见图4。

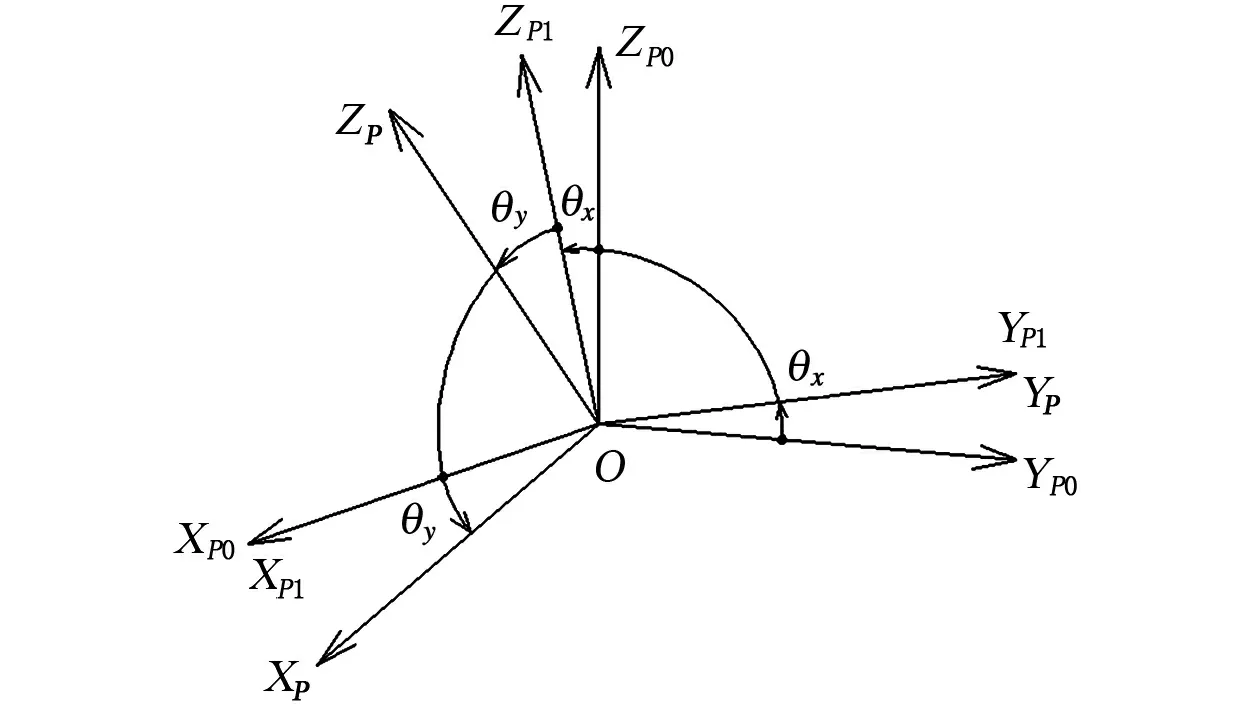
图4 自调平台调平时各框坐标系的转换示意图Fig.4 Coordinate transformation of self-stabilization platform platform shafting system

平面基准镜固定在船体上，自调平台的基座也固定在船体上，一般认为基准镜与自调平工作台之间的船体是刚性体，那么两者可以认为是固联在一起。在某一时刻，在经纬仪对平面镜进行自准直测量时，经纬仪的望远镜指向与平面镜法线相反，那么在测量过程中，平面镜在内框坐标系OXPYPZP内方位角的变化量即可认为经纬仪方位角的变化量。

为了说明在对平面镜测量时经纬仪的方位角变化情况，也就是基座发生摇摆后，调平台通过中框、内框的角度变化将内框调平的过程，通过坐标变换，将平面镜法线的矢量反方向转换到内框坐标系下。

为了简化计算，先假设基座处于静止状态，台体轴OZP处于垂直位置，内框坐标系OXPYPZP分别与中框坐标系OXP1YP1ZP1和基座坐标系OXP0YP0ZP0相重合，假设平面镜法线在OXP0YP0ZP0坐标系下的的向量为

(1)

平面基准镜法线在XP0YP0ZP0坐标系下的定义见图5。

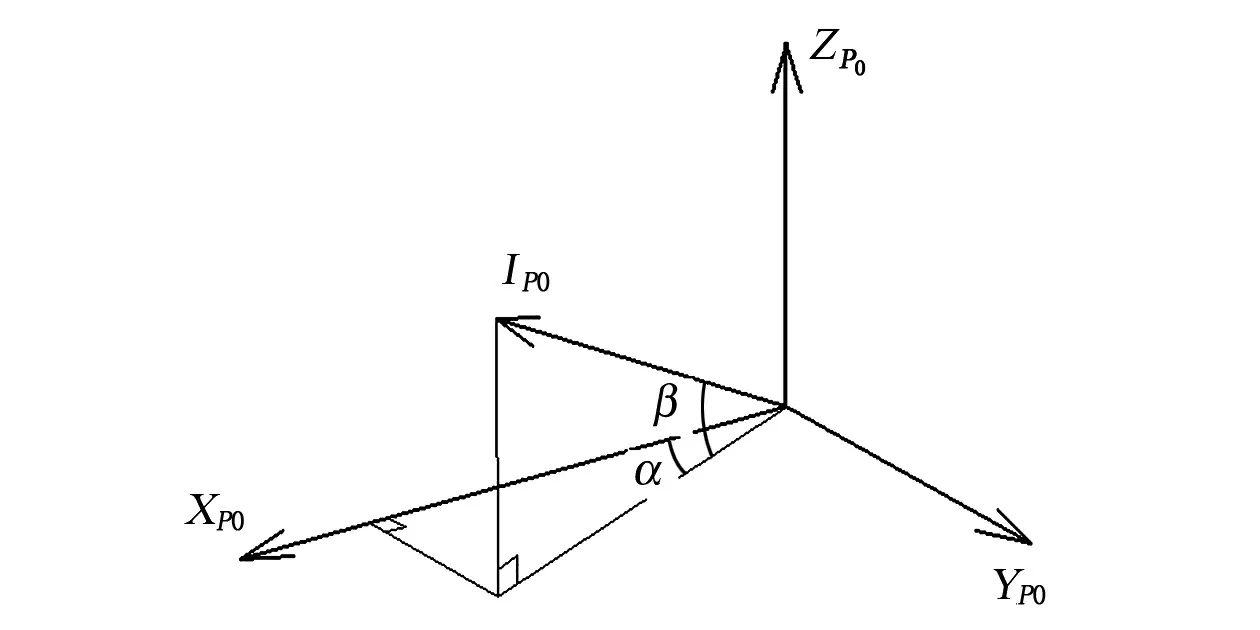
图5 平面镜法线在XP0YP0ZP0坐标系下的定义Fig.5 Plannar mirror normal line definition in the XP0YP0ZP0coordinate system

初始状态下，平面镜法线投影到OXPYP平面内，与OXP轴的方位夹角为α。

当中框架绕OXP0轴旋转θx时，旋转矩阵为[2]

(2)

基准平面镜法线在OXP1YP1ZP1坐标系下的向量为

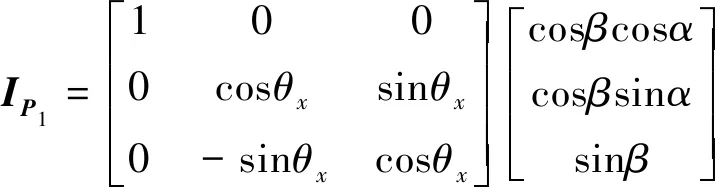
(3)

当内框绕内框轴OYP旋转θy时，旋转矩阵为

(4)

基准平面镜的法线在OXPYPZP坐标系下的向量为

(5)

方位角为IP投影到OXPYP平面内与OXP轴的夹角，即为

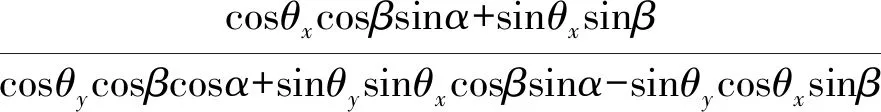
(6)

由上式可看出，经过转换，方位角发生了变化，但式中未知参数较多，下面将根据具体使用情况进行分析。由于船的纵横摇角度一般在几度的量级，例如在某船上的测量，一般要求船的横摇角不大于4°、纵摇角不大于3°。那么，在调平过程中，调平台的回调量θx<4°，θy<3°。在经纬仪的使用过程中，为了便于操作和减少大俯仰角对方位传递的影响，一般进行平瞄操作，即β=0°。当β=0°时，式(6)可简化为

(7)

方位角Ip投影到OXPYP平面内与XP轴的夹角，即为

(8)

3 调平台的初始安装位置对测量方位角的影响

3.1 调平台的初始安装角α对测量方位角的影响

实际使用过程中，基准平面镜法线的俯仰角很难调整到α=0°，β=0°，那么，先以β=0°，纵摇θy=2°，横摇θx=3°，分析α角度带来的影响。

当β=0°，θx=3°，θy=2°时，影响结果见表1。

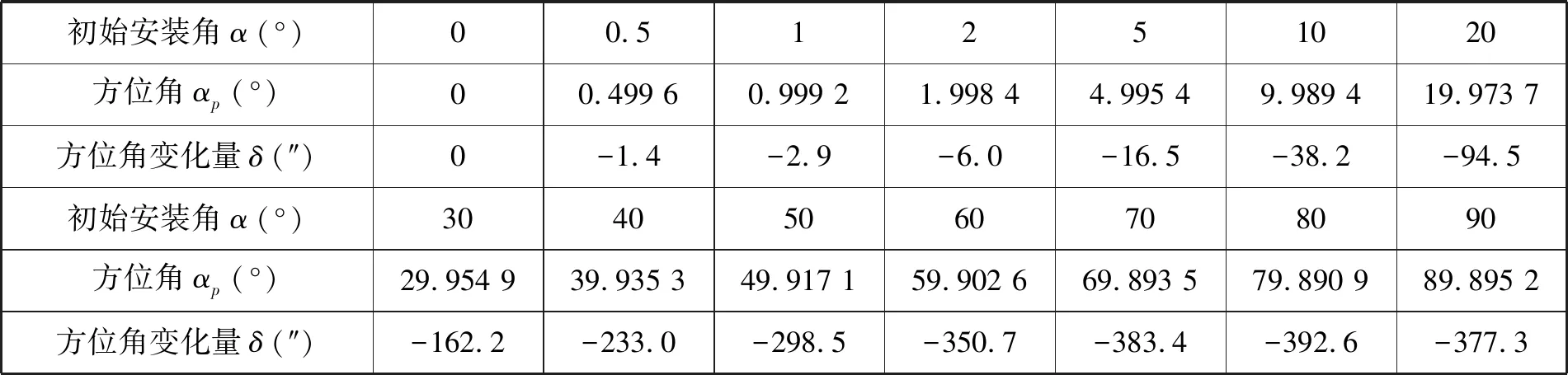
表1 初始安装角α对方位角变化量的影响Tab.1 Effect of primary installation angleαon azimuth angle variationδ

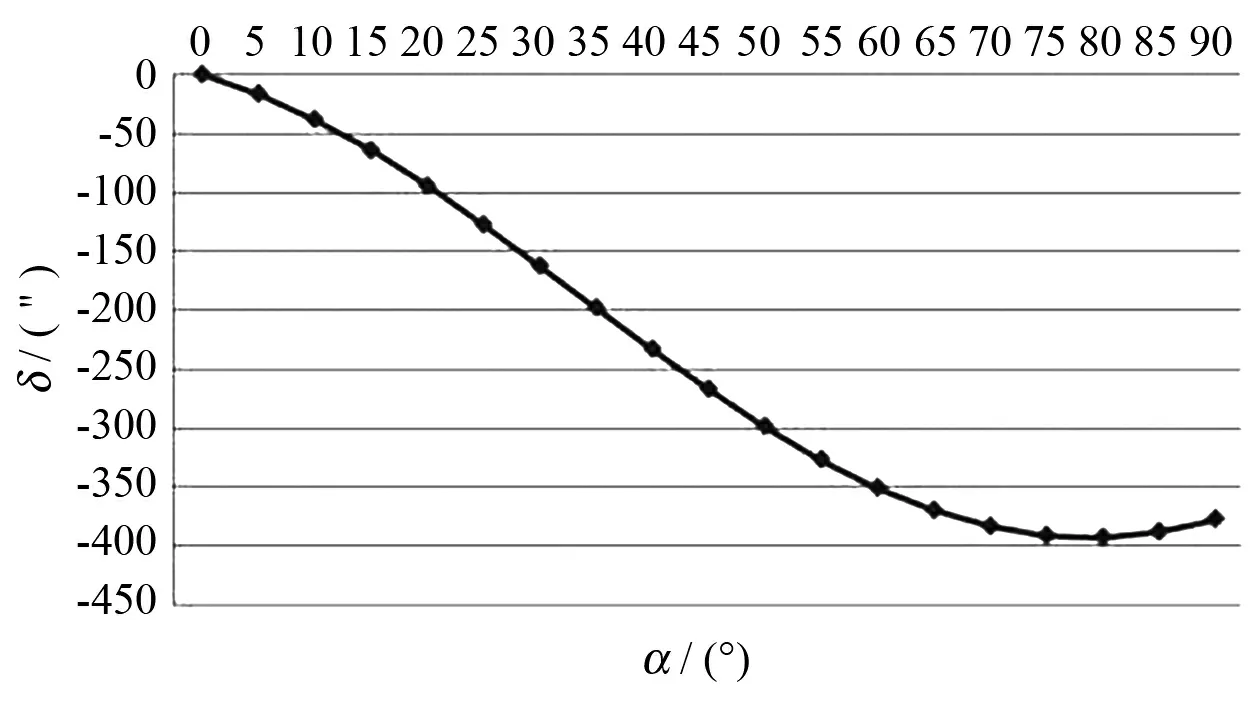
图6 在船横摇3°、纵摇2°，平面镜俯仰角为0°时， 方位角随其初始方位指向的变化量Fig.6 Azimuth angle variation with primary azimuth pointing,when roll angle is 3°,pitch angle is 2°， plannar mirror primary azimuth angle is 0°

由图6可以看出，在0°～90°的范围内，平面基准镜的初始方位角越大，在纵横摇具有一定的角度时，其方位角的变化量越大。因此，在进行调平台的安装时，应尽量使调平台基座的XP0轴与平面基准镜的法线方位一致，即使α的值接近于零。

3.2 调平台的安装角β对测量方位角的影响

然而在实际操作时，很难将α调到0°，那么，假设α=0.5°，在横摇角θx=3°，纵摇角θy=2°的情况下，分析方位角的变化量δ随β的变化情况，由于β为平面基准镜的俯仰角，该角度可以通过调整使其接近于0°，影响结果见表2。

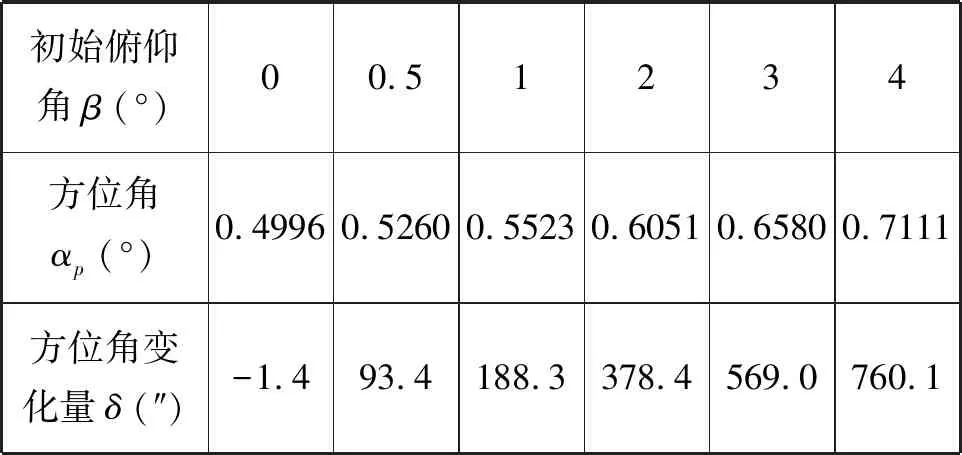
表2 初始俯仰角β对方位角变化量δ的影响Tab.2 Effect of primary pitch angleβ on azimuth angle variationδ

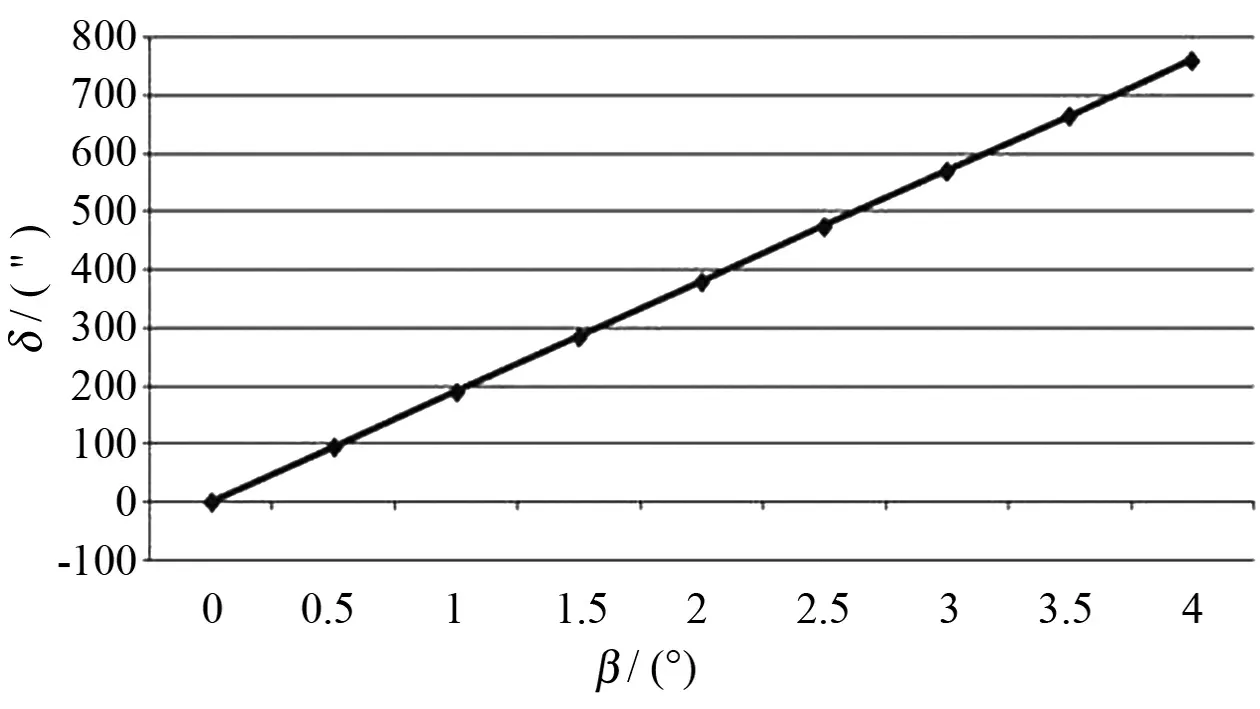
图7 在船横摇3°，纵摇2°时，平面镜初始方位角为0.5°时， 其方位角随其初始俯仰指向的变化量Fig.7 Azimuth angle variation with primary elevation pointing,when roll angle is 3°,pitch angle is 2°, plannar mirror primary azimuth angle is 0.5°

由图7可以看出，在俯仰角0°～4°的范围内，平面镜的初始俯仰角越大，在纵横摇具有一定的角度时，其方位角的变化量越大。因此，在进行调平台的安装时，应尽量使调平台基座的OXP0轴与平面基准镜的法线俯仰一致，即使β的值接近于零。

4 纵横摇对测量方位角的影响

以上α、β角跟自调平工作台的初始安装有关，安装完成固定后，这两个角度不再发生变化，在测量过程中，船一直处于摇摆状态，摇摆角θx、θy的变化是随机过程，下面将分析纵横摇角度对测量方位角的影响。

4.1 横摇对测量方位角的影响

由于在船上调平台的安装，很难做到α=0°，β=0°，那么，假设以α=0.5°、β=0.2°为初始安装角度，为了便于分析，假设纵摇角θy=2°。由于横摇角一般不大于3°，因此分析横摇角在0°～3°范围内对方位角的影响情况，影响结果见表3。

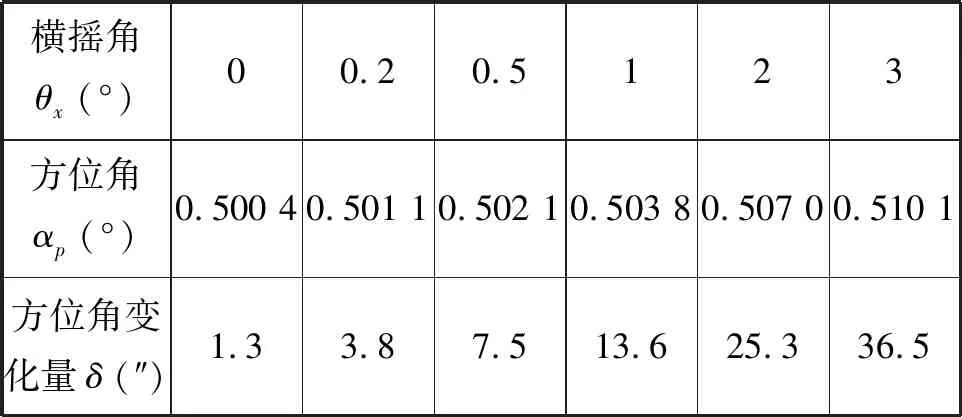
表3 横摇角θx对方位角变化量δ的影响Tab.3 Effect of roll angle azimuth angle variation

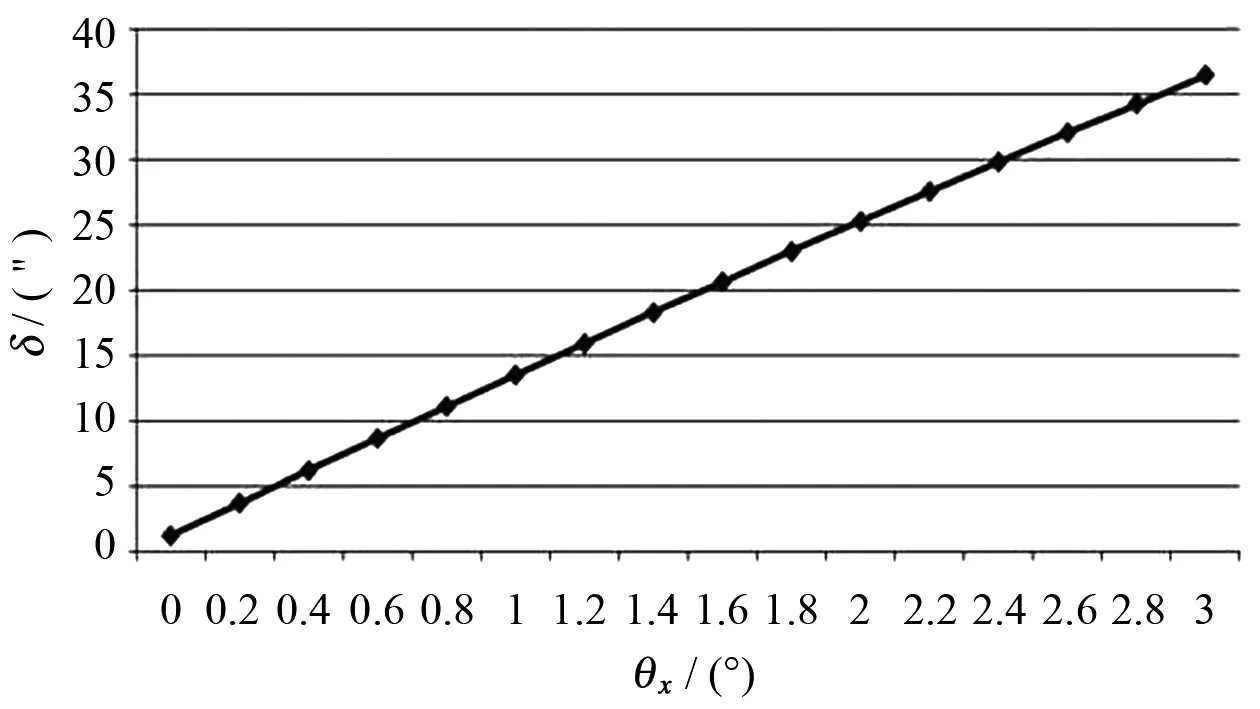
图8 在纵摇2°时，平面镜初始方位角0.5°、 初始俯仰角0.2°时，其方位角随船横摇的变化量Fig.8 Azimuth angle variation with roll angle,when pitch angle is 2°, plannar mirror primary azimuth angle is 0.5° , primary elevation angle is 0.2°

由图8可见，在纵摇角不变的情况下，横摇角越大，由此而带来平面基准镜方位角的变化越大。

4.2 纵摇对测量方位角的影响

同样，假设α=0.5°，β=0.2°，θx=2°，分析方位角受纵摇角影响的情况，由于纵摇角一般不大于2°，因此分析横摇角在0-2°范围内对方位角的影响情况，影响结果见表4。

由图9可见，在纵摇角、平面镜初始方位角、初始俯仰角一定的情况下，方位角的变化量受纵摇角的增大而增大，但影响系数不大。

表4 纵摇角θy对方位角变化量δ的影响Tab.4 Effect of pitch angle on azimuth angle variation

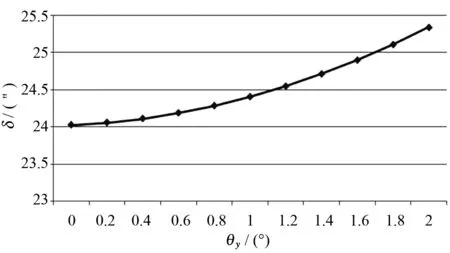
图9 在横摇2°时，平面镜初始方位角0.5°； 初始俯仰角0.2°时，其方位角随船纵摇的变化量Fig．9 Azimuth angle variation with pitch angle,when roll angle is 2°, plannar mirror primary azimuth angle is 0.5° , primary elevation angle is 0.2°

5 结束语

在动机座条件下，自调平台为经纬仪提供水平基准，为经纬仪的正常使用提供了必要条件，但是经纬仪在对船上固定的基准镜测量传递角度基准时，纵横摇对传递结果造成一定的误差，该误差值的大小随纵横摇角度的变化而变化。

根据上文中对误差影响因素的分析，在动机座环境下，以自调平台作为水平基准、利用经纬仪对方位角测量传递，为了减小纵横摇带来的误差，自调平台的安装时应遵循以下原则：

(1)自调平台的安装时，使其基座的XP0尽量与被测镜的法线平行。即经纬仪调平底座的内框轴轴线与被测反光镜的法线平行。根据第3节中的计算，当经纬仪的测量镜筒指向与调平底座中框轴轴线之间的夹角越小，纵横摇带来的误差也越小。

(2)为了避免基座的XP0与被测镜的法线不平行，在调平台安装空间位置受限，不能直接对反射镜测量时，在测量光路上加折转光管，折转光管能够保持光路的方向不变，即测量方位角的方向不变，以减小调平台的安装初始角度α。

(3)对于传递方位角的两台经纬仪调平台的放置方向，内框轴和中框轴的方向应尽量一致。通过对第3节中的计算结果分析可知，调平台不同的安装初始角度α，纵横摇给经纬仪引入的误差量是不同的，那么，在两台经纬仪对瞄进行传递方位角时，如果两者的初始安装方位角不一致，那么两者之间将存在测量误差，误差量的大小与两调平台的相对角度有关。

(4)通过自调平台测量纵横摇角度，进行误差补偿。由自调平台设置调平零位，自调平台处于零位时，基座坐标系、中框坐标系和内框坐标系重合。调平过程中，如果能够实时采集中框、内框与零位的角度偏移量，即纵横摇角度，通过文中公式(6)计算产生的误差量，用于对测量方位角度的补偿修正。

另外，由文中的分析可知，自调平台带来的误差根源在于船体的纵横摇，如果能够实时测量出船体的纵横摇角度，通过坐标转换可以对测量的方位角进行补偿。因此，为解决动基座带来的方位角测量问题，还可以采用以下方式：利用动机座姿态测量仪实时测量船体姿态，将测量到的方位角投影到水平坐标系里。该方法可以不使用自调平工作台，也就不需要考虑自调平台安装方向、经纬仪对瞄方向等问题，但前提是具有高精度的动基座姿态测量仪，如船上的惯性导航系统，并且要保证方位角测量仪器的竖轴一致，即要为经纬仪、姿态测量仪等提供高精度、统一的基准面，这需要船在坐墩的情况下才能保证，因此该方法的实现也具有一定的复杂性。