小型混合翼无人机过渡过程一体化建模与控制

王博豪 张 勇 徐伟程 郭 锦

(1.南京航空航天大学自动化学院，南京 210016；2.南京航空航天大学无人机研究院，南京 210016；3.中小型无人机先进技术工业和信息化部重点实验室，南京 210016)

1 引 言

当下无人机发展势头迅猛，无人机按照飞行平台机构可分为固定翼无人机、旋翼无人机、无人飞艇、伞翼无人机、扑翼无人机等[1]。其中近年来固定翼无人机和旋翼无人机因飞行特性好、稳定性高发展尤为迅速。多旋翼无人机前飞速度较慢，而且由于现有电池容量有限，航程和航时受到限制。固定翼无人机拥有较快的前飞速度，固定翼无人机航时和航程是多旋翼无人机的二到三倍，但是起飞和降落一般采用滑跑起飞的方式，在应用时往往会受到场地的影响而无法使用。

为解决固定翼无人机和旋翼无人机的缺点，混合翼垂直起降无人机应运而生。混合翼垂直起降无人机相对倾转旋翼无人机具有结构简单的特点，只需要在原来固定翼结构上加装旋翼部分即可。对复合式垂直起降无人机过渡过程定性的建立了六自由度动力学方程，提出了一种过渡方案，对一些典型的技术问题，提出了相应的对策；对旋翼和固定翼分别建模，采用旋翼只提供升力不产生力矩的控制策略，为保证无人机姿态让无人机总升力与重力相等，仅通过控制固定翼的舵面控制无人机姿态，但由于转换初期速度较低，机翼尾翼调整能力有限，旋翼提供升力不产生力矩，导致前期姿态波动较大；对垂直起降模式和固定翼模式分别建模，在过渡过程起始阶段仅依靠旋翼部分提供前飞和保持姿态稳定，在达到合理的速度后直接切换为固定翼模式，但旋翼和固定翼为两个完全不同的模型，直接切换会使系统输入和状态量产生突变，无法保证系统的稳定性。本文在过渡过程中旋翼部分和固定翼部分同时对无人机施加力和力矩，将旋翼部分和固定翼部分进行整体建模，建立了过渡过程旋翼和固定翼共同控制无人机状态的六自由度模型，然后对纵向运动模型进行配平和小扰动线性化，并对得到的纵向过渡过程模型进行稳定性分析，最后设计了基于增益调度的LQR全状态反馈控制器。通过仿真验证，所设计的控制器能够满足设计要求。

2 数学建模

由于旋翼部分和固定翼部分的控制面和系统输入均不同，导致两模型差异较大。在前飞速度增大的转换过程中，切换两个模型会使无人机状态发生突变，无法保证无人机的稳定性。将旋翼和固定翼整体建模，让旋翼和固定翼共同控制无人机姿态，使过渡过程更加平缓，并保证过渡过程的稳定性。

混合翼垂直飞降无人机试验样机如图1所示。

图1 混合翼垂直起降无人机试验样机Fig.1 Hybrid wing vertical take-off and landing unmanned aircraft test prototype

对于无人机平动有

(1)

将上式展开得

(2)

式中：Fx、Fy、Fz——分别为无人机在机体坐标系下沿机体轴方向受力的分量；u、v、w——分别为沿机体坐标轴方向上的速度分量；p、q、r——分别为沿机体坐标轴各方向上的角度分量。

(3)

式中：Ffx、Ffy、Ffz——分别为固定翼在机体轴三个方向上的分力；Fxz、Fyz、Frz——分别为旋翼在机体轴三个方向上产生的升力[6]。

对于无人机绕质心的运动有

(4)

(5)

式中：L、M、N——无人机受力矩在机体坐标轴上的投影；J——惯性矩阵。

(6)

式中：lf、mf、nf——分别为固定翼产生的滚转、俯仰、偏航力矩；lr、mr、nr——分别为旋翼产生的滚转、俯仰、偏航力矩。

过渡过程纵向运动方程组为

(7)

(8)

(9)

(10)

(11)

式中：T——固定翼推力；D——无人机所受阻力；α——迎角;θ——俯仰角;V——惯性坐标系前飞速度。

复合式垂直起降无人机的前飞速度是过渡过程中的重要特征参数，无人机过渡过程前飞速度由0加速，加速到固定翼起飞速度即18m/s，随着速度的增大，固定翼机翼产生的升力越来越大，需要给定相应的旋翼油门保持合理的飞行姿态。将纵向运动方程组在速度V=[0,18]m/s范围内进行配平，并对配平状态进行线性化，线性拟合得到关于前飞速度V的状态空间表达式

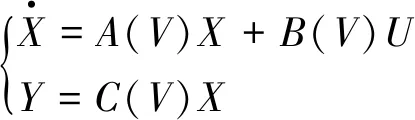
(12)

系统状态X=[Vαqhθ],输入U=[teT1T2]。其中t为固定翼油门，e为升降舵输入，T1、T2分别为前边一对和后边一对的旋翼油门。

由图2可以看出，在前飞速度V=[0,18]m/s范围内，系统存在实部大于0的特征根，即在速度变化过程中存在不稳定状态。不同前飞速度系统状态相差较大，传统的线性时不变控制器无法得到满意的控制效果。

图2 不同状态下系统特征根在复平面分布Fig.2 Distribution of the eigenvalues of the system in the complex plane under different states

3 控制器设计

由以上对系统特征值分析可知，单一的线性控制器无法使系统在参数进行大范围变化时得到良好的跟踪效果。采用基于LQR的增益调度策略设计控制器，将系统参数变化较大的非线性系统分成多个部分，降低系统参数的变化范围，然后在各部分进行配平和线性化，得到相应的线性时不变系统，针对各个线性时不变系统设计LQR控制器。线性时不变控制器能够在一定范围内对非线性系统进行良好的控制，根据非线性系统的参数变化，来切换相应的线性控制器，从而控制整个非线性系统[7～10]。

对于各部分能控能观线性系统，其状态方程有如下形式

(13)

式中：X∈Rn——n维状态向量;Y∈Rm——m维输出向量;U∈Rr——r维控制向量;A0，B0，C0，D0——分别为n×n维，n×m维，m×n维，m×r维常数矩阵[11]。

为使前飞速度和高度跟踪指令信号，令前飞速度和高度输出y=(V,h)和指令信号yr=(Vr,hr)的误差为

e=yr-y

(14)

设计能量函数J

(15)

式中:Q、R——分别为n×n维，m×m维对角矩阵;Q——半正定矩阵;R——正定矩阵。目标函数的意义在于使用较小的输入量使得系统的状态量有尽可能小的误差，所以当取得能量函数J最小时，目标成立[12～14]。

为了让能量函数最小，需要引入λ构造Hamilton函数

(16)

通过解Riccati方程和n维向量得

(17)

(18)

系统的输入为

(19)

则状态反馈增益矩阵可以表示为

(20)

系统最优跟踪轨迹线是以下微分方程的解

(21)

以前飞速度V=15m/s，高度h=10m为例，对系统进行配平和小扰动线性化，得到无人机在该状态下的纵向系统状态空间矩阵

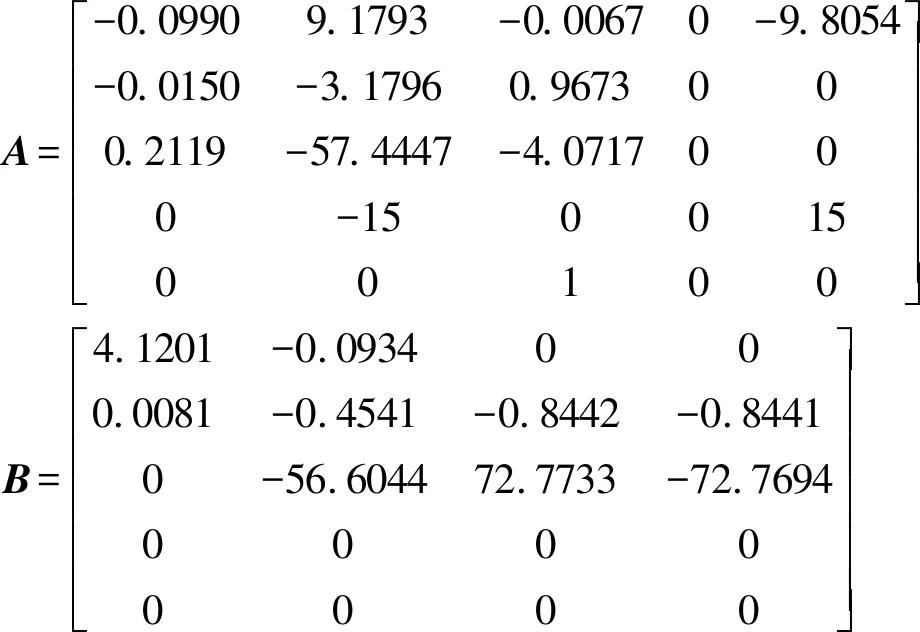
选取控制系统状态有关的权重矩阵Q=diag(1,1,1,1,1)，和系统输入有关的权重矩阵R=diag(1,1,1,1)，通过计算得到系统的反馈增益K

同理，为使过渡过程相对平滑，在定高状态下，选取前飞速度为3m/s，6m/s，9m/s，12m/s，15m/s，作为无人机工作点进行配平。在各配平点采用设计相应的控制器。通过切换控制器来实现以前飞速度为参考的增益调度。控制结构如图3所示。

图3 控制器结构Fig.3 Controller structure

系统初始状态X=[0;0;0;10;0]。前飞速度设定为斜率为3的斜坡信号，达到18m/s时保持。系统仿真结果如图4～图6所示。由下图可以看出，在加速阶段无人机前飞速度可以在各速度下得到不错的跟踪效果，在8s和10s时加入阶跃输入，同样可以得到良好的跟踪效果。无人机纵向高度在加速阶段会出现掉高，在第12s加入阶跃信号，无人机高度有一定的超调，没有静态误差。

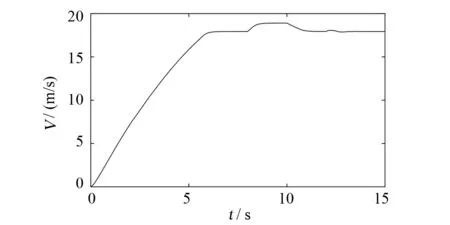
图4 混合翼无人机过渡过程速度随时间响应曲线Fig.4 Velocity response curve of hybrid wing UAV in transition process

图5 混合翼无人机过渡过程高度随时间响应曲线Fig.5 Height response curve of hybrid wing UAV in transient process

图6 混合翼无人机过渡过程俯仰角随时间响应曲线Fig.6 Pitch angle Height response curve of hybrid wing UAV in transient process

4 结束语

本文对小型混合翼垂直起降无人机的过渡过程进行了一体化整体建模，推导了六自由度非线性动力学方程，进行配平和小扰动线性化，对得到的数学模型进行稳定性分析。采用基于LQR的增益调度控制，对无人机的速度和高度进行跟踪控制，有仿真结果可知前飞速度在加速和匀速阶段都有良好的跟踪效果。无人机在前飞加速过程高度有约0.2m的掉高，且在跟踪过程中存在超调。俯仰角在加速阶段波动较大，需要改进控制方法，改善高度和俯仰角的控制效果。