考虑多类应急物资需求不确定的选址模型

孙清臣，曲林迟

(上海海事大学经济管理学院， 上海201306)

0 引言

重大自然灾害发生后，灾区民众需要大量物资维持正常生活。我国自然灾害种类多、发生频率高、分布地域广，有效配置应急资源是提高政府应急物资保障能力的重要手段。储备库布局、物资储备种类和数量的决策，决定着处置救援的效率。

目前，应急物资配置相关的文献主要研究储备库选址、库存管理、采购模型及协议企业选择等问题。Döyen等[1]提出两阶段随机规划模型，优化灾前和灾后救援中心选址、应急物资库存和灾后物资配送决策。陆相林等[2]基于设施选址理论，以应急物资需求点和民众总体满意程度最大为目标，构建考虑交通方式、需求点风险程度的市域应急物资储备库选址模型，优化储备库布局。张鑫等[3]基于联系数的区间灰数法预测不确定需求，构建包含最短应急时间、最大覆盖范围、最小成本的多目标应急物资储备库模型，利用改进的非支配排序遗传算法求解模型。葛洪磊等[4]提出基于情景的两阶段随机规划模型，优化应急物资储备设施选址及物资分配方案。Roni等[5]研究考虑常态和应急订货点的混合库存管理策略，以为协议企业同时应对常态和应急需求提供决策支持。Falasca等[6]提出两阶段随机决策模型，优化灾后物资采购决策。田军等[7]将实物期权契约引入到由政府和供应商组成的非营利性供应链，提出基于实物期权契约的应急物资采购模型，为政府确定合理的期权价格策略提供决策依据。应急物资的采购决策受多种因素影响，如数量折扣和运输成本[8]、汇率[9]、交货期和服务水平[10-11]等，考虑这些因素有助于选择更合适的应急物资协议企业。Balcik等[12]考虑不同企业物资供应数量、交货期、价格的差异，提出两阶段随机规划模型，优化代储企业布局。已有研究较少综合考虑储备库选址、物资储备种类和数量，以及物资配送等问题。

若不对上述问题进行综合考虑，易造成处置救援效率低下。例如，若储备库选址不合理，易造成物资输运成本高昂并难以保证物资及时运抵灾区；若不综合考虑物资储备种类和数量，易造成物资的储备不均衡，导致灾区的某类物资供应不足。综上，本文考虑需求量和受灾地的不确定性构建灾害情景，建立两阶段随机规划模型，优化储备库选址、不同类型物资的储备量和物资的配送等决策，提出样本均值逼近方法并设计算例证明方法的性能。

1 应急物资储备库选址模型

集合和参数定义如下。I为位置集合，i,j∈I；A为应急物资种类集合，a∈A；L为储备库类型集合，l∈L；S为自然灾害情景集合，s∈S；ωs为情景发生概率；Dj,a,s为情景s下，位置j的a类物资需求量。CFl为l型储备库的造价；Ql为l型储备库的储备能力；Na为a类物资的体积；CPa为a类物资的零售价格；CTa为单位物资的运输价格；CHa为单位物资的持有价格；Ga为a类物资供应不足的单位惩罚系数。Hi,j为位置i到j的距离；δ为采购折扣率。

决策变量定义如下。是否在位置i建立l型储备库xi,l，若建立，xi,l=1，否则xi,l=0；位置i的a类物资库存ei,a。情景s下，从储备库i运往位置j的a类物资量pi,j,a,s，位置i的a类物资剩余量zi,a,s，以及位置i未满足的a类需求量wj,a,s。

(1)

(2)

(3)

(4)

(5)

(6)

(7)

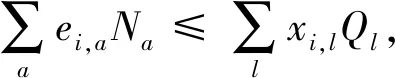
(8)

(9)

(10)

xi,l∈{0,1},i,l,

(11)

ei,a,pi,j,a,s,zi,a,s,wi,a,s≥0, ∀i,j,a,s,

(12)

F为总成本，fc为固定成本，pc为采购成本，tc为运输成本，hc为库存成本，wc为惩罚成本。基于我国的实际情况，一个城市至多存在一个中央级救灾物资储备库。因此，式(7)限定每个位置最多建立一种类型的储备库。式(8)限定物资库存不超过储备库的容量。储备物资的剩余量为库存与运输量的差值，计算方式见式(9)。物资供应不足的量为需求量与运输量的差值，计算方式见式(10)。由于储备库只能为建立或不建立，所以式(11)限定x只能取0或1。由于库存、运输量、剩余量和供应不足的量均不能为负数，所以设置式(12)为非负约束。

2 样本均值逼近法

样本均值逼近法(sample average approximation, SAA)，生成多个独立同分布的样本，利用样本均值函数替代原问题的目标函数，求解样本问题，选取样本最优解作为原问题的近似解。SAA方法步骤如下：

Step1:生成|K|个概率分布为p的独立样本M，每个样本包含|M|个情景；

Step3:生成一个较大的样本M′(需满足|M′|≫|M|)以验证样本最优解。对任意k∈K，分别求解模型(14)；

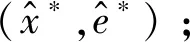
Step5:使用式(16)计算估计目标值与最优目标值的差异率，以评估近似解的优劣。

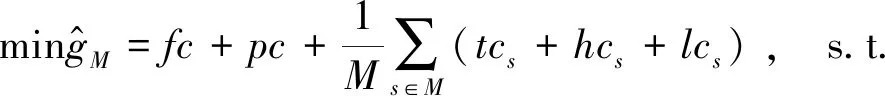
(13)

(14)

(15)

(16)

3 算例分析

3.1 参数设置

根据2008年的南方雨雪冰冻灾害、汶川地震、华南和中南地区洪水，以及台风“黑格比”4种自然灾害的转移安置人口及各省实际受灾程度[13]，设计自然灾害情景，进行算例分析。考虑3类应急物资，1表示日常消耗类物资，如食物、水、卫生用品等；2表示生活类物资，如帐篷、毯子、大衣、照明设备和蚊帐等；3表示医疗类物资。第1、3类物资，每人的需求为一个单位；第2类物资，每4人的需求为一个单位；受灾人口的1/8需要第3类物资。不同情景的发生概率及各省第1类物资的需求量[14]见表1。集合|I|=14，|A|=3，|S|=16。

表1 不同情景的发生概率及各省第1类物资的需求量(单位需求量)Tab.1 Demand for type 1 item with provinces and probability for scenarios

假设各省都可建立小、中、大3类储备库，则|L|=3。储备库的造价CFl={10,20,30}万元，储备库容量Ql={50 000,130 000,250 000}m3，物资体积Na={0.1,1,0.5} m3，零售价格CPa= {2,500,2 000}元，运输价格CTa={0.022 5,0.09,0.022 5}元/km，持有价格CHa={0.5,5,100}元，供应不足的单位惩罚系数为零售价格的10倍，采购折扣率δ=90 %。省份i到j的距离通过百度地图计算两省省份城市间的距离。

3.2 算例结果分析

应用Cplex 12.6求解情景|S|=16的算例，运算时间少于5 s。不同省份的储备库类型及物资储备，如表2所示，唯一的大型和中型储备库分别位于重庆和云南，且储备了最多的第2和第3类物资。这是由于灾害情景造成西南各省的受灾人数最多，物资需求量大，为降低物资供应不足风险，需建立具有较大仓储能力储备库，且储备大量救灾物资。

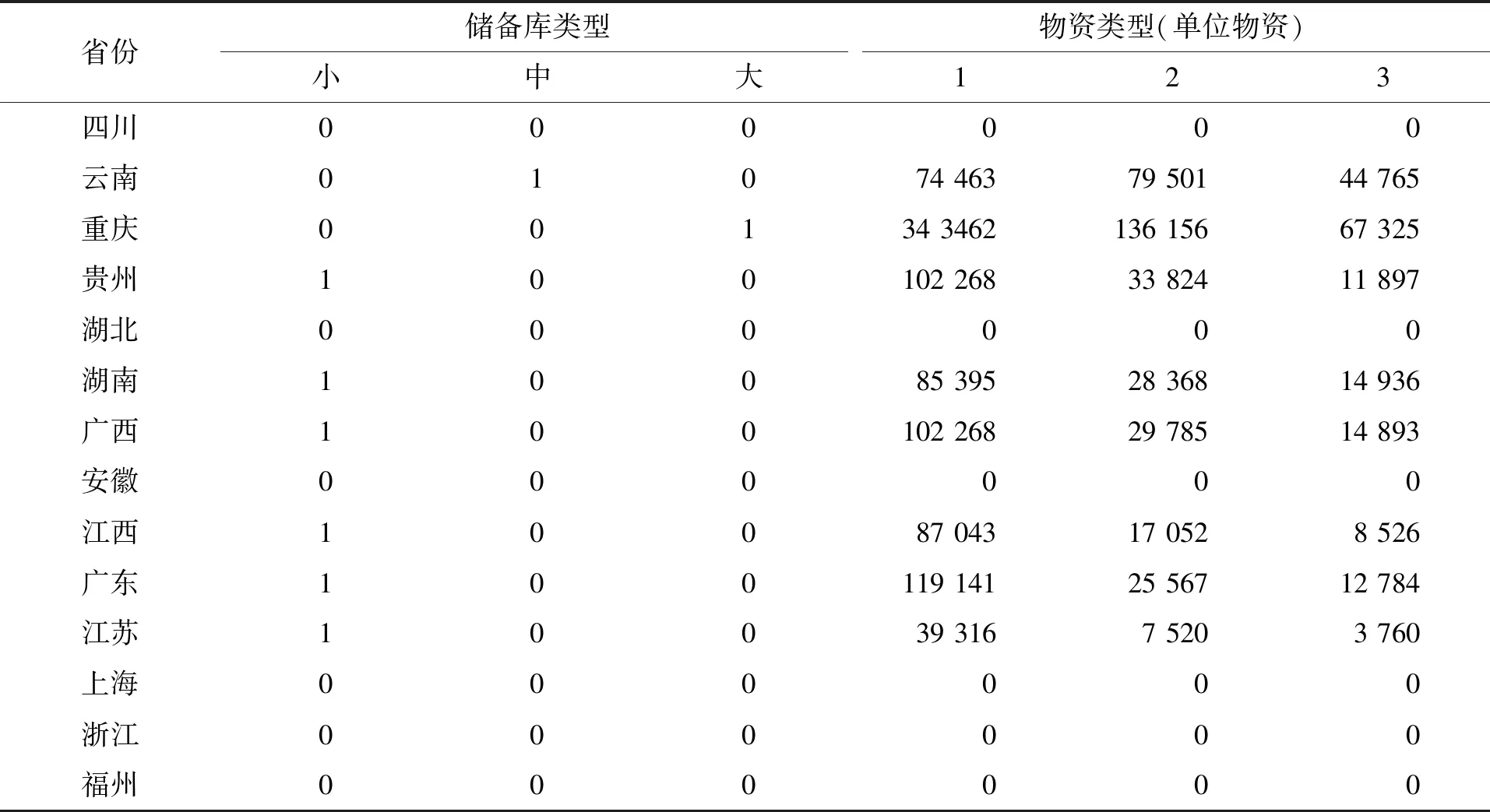
表2 不同省份的储备库类型及物资储备Tab.2 Warehouse location and inventory for provinces

不同采购折扣率下各成本变化率，如表3所示。当采购折扣率为0.9时，固定成本、采购成本、持有成本、运输成本和惩罚成本分别为110、53 857、1 233、810、13 708万元。与0.9的采购折扣率相比，当折扣率减少，经济成本降低，惩罚成本增大，物资供应量急剧增大。当无法获取采购折扣率(即采购折扣率为1时)，惩罚成本增大了78.61 %；而当折扣率增大，各成本无显著变化。上述结果表明，政府获得更大的折扣率并不总是有利于大幅降低物资供应不足的风险。

表3 不同采购折扣率下各成本变化率Tab.3 Variation of costs with different procurement discounts 万元

经济成本与惩罚成本存在二律背反，即经济成本的增大或减小会造成惩罚成本的减小或增大。因此，以式(17)代替式(1)，研究风险权重γ的变化对经济成本、惩罚成本和总成本的影响。分别设置γ=0.1,…,0.9,1，求解模型，不同惩罚成本权重下经济成本和惩罚成本的变化趋势，如图1所示。

(17)

权重对经济成本和惩罚成本的影响可分为[0.1,0.4]、(0.4,0.8)和[0.8,1]3个阶段，当权重从0.1增大至0.4，经济成本增加391 %，降低了88 %的惩罚成本；权重在(0.4,0.8)范围内取值，经济成本和惩罚成本无显著变化；权重从0.8增大至1，增加493 %的经济成本仅可降低10 %的惩罚成本。若想完全避免因物资供应不足造成的风险，需投入176 056万元。结果表明适当考虑惩罚，可降低物资供应不足的风险；但是，过度追求风险最小，需要大量投入资金以储备物资，若长时间内无自然灾害发生，易造成资源浪费。

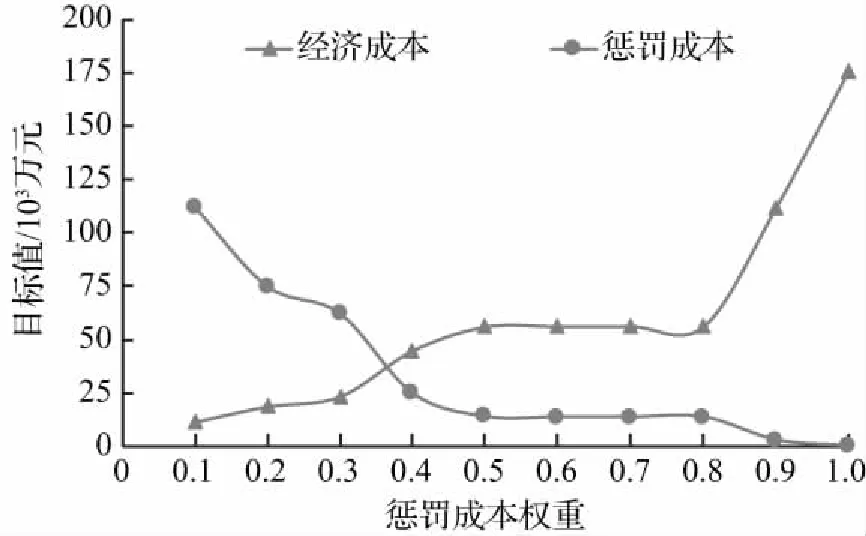
图1 不同风险权重下经济成本和惩罚成本变化趋势Fig.1 Tendency of economic costs and penalty costs with different risk weight

3.3 SAA法有效性分析

当|I|=20，|S|=100时，Cplex 12.6求解原问题耗时351 s，最优目标值为31 185.64万元。应用Matlab编译SAA方法，设置|M|=10时，不同|K|值的求解结果，如表4所示。与Cplex的计算结果相比，|K|≤30时，近似目标值与最优目标值之间的差异率不超过0.033 %，且SAA方法耗时更少，可至少节约14 %的计算时间。由于样本情景选取具有随机性，当样本情景数不变，样本数越大，仅有更大的概率获得更好的近似解，但难以保证近似解的质量。例如，样本数为25的估计目标值优于30。

表4 不同|K|值的求解结果Tab.4 Results for different value of |K|

设置|K|=10，不同|M|值的求解结果，如表5所示。当(|K|,|M|) = (10,25)，估计目标值与最优目标值的差异率仅为0.005 %。当样本数量不变，样本的情景数量越多，样本的估计目标值逐渐接近最优目标值，可有效降低样本选取随机性的影响，因而候选解的质量越高， 但是，SAA法会耗时更多。例如，与|M|=20相比，|M|=25的计算时间增加了20 %。此外，可通过调整样本数或样本的情景数，以满足对差异率或计算时间的要求。

表5 不同|M|值的求解结果

4 结论

本文综合物资的储备库选址、不同类型物资的库存和物资配送等问题，建立基于情景的两阶段随机规划模型，构建SAA方法求解模型，设计自然灾害情景进行算例分析。结果表明，获取一定的采购折扣率有助于降低物资供应不足的风险；过度追求风险最小化，会大幅提升物资采购和储备成本，易造成物资浪费；与Cplex相比，SAA方法能在较短时间内获得较好的近似解。下一步研究方向，模型中可考虑配送路径问题，以增加模型的实用性；在SAA方法中应用更高效的算法求解样本问题，以提高计算效率。