高边坡时序位移滚动预测的SVM-Elman模型
22
(1.河海大学 水文水资源与水利工程科学国家重点实验室, 南京 210098;2.河海大学 水利水电学院,南京 210098;3.浙江省桐乡市水利局, 浙江 桐乡 314500)
1 研究背景
岩体高边坡在内部因素(岩土体的地质缺陷、岩体与基岩的徐变、蠕变、土体渗透和压缩变形等)与外部因素(温度、水压、降雨等)的共同作用下变形十分复杂,且各因素具有模糊和随机波动的特征。边坡位移反映了边坡变形,基于边坡位移时间序列建立科学的分析模型,对预测预报边坡的发展趋势和演变规律,及时掌握边坡的变化规律有着重要的意义。针对边坡位移预测,常用的主要建模方法有:位移时间统计分析法[1]、灰色聚类评价法[2]、人工神经网络及各预测方法的组合等[3-5]。由于边坡系统的复杂性,这些方法难以完全准确可靠地确定边坡位移与其影响因素间的关系,如灰色聚类评价法主要用于指数型时间序列,对于复杂非线性波动的边坡位移序列往往无法得到合理的预测结果;BP等人工神经网络属于非启发式算法,缺乏严密的理论基础,需要大量的学习样本,而获取大量有代表性的边坡位移监测值存在困难[6],所以预测精度难以保证。
支持向量机[7-10](SVM)采用结构风险最小化的原理,既能将有限训练样本的误差降为最低,又能保证独立测试样本的误差最小,同时对于解决高维度非线性问题也有很强的适应性。Elman神经网络属于反馈型动态神经网络,能通过存储内部状态使系统具备适应时变特性的能力。本文尝试将这2种算法组合起来,提出了SVM-Elman神经网络预测模型。首先通过粒子群优化(Particle Swarm Optimization,PSO)算法优化SVM预测模型,确定模型参数并对边坡位移监测数据进行学习和拟合,滚动预测边坡位移的总体走势规律;在此基础上利用Elman神经网络的适应时变的能力,寻找样本SVM预测值与监测值相对误差的后续走势规律,从而达到缩小位移时序相对误差的目的;最后本文以算例验证该方法的有效性。
2 SVM-Elman神经网络模型构建
2.1 SVM位移时序拟合
2.1.1 SVM时序拟合基本原理
y=ωTφ(x)+b。
(1)
式中:ω为权向量;b为偏置项。
在考虑允许误差存在的条件下,将训练样本的误差控制在精度ε下线性拟合,该问题就转化为一个凸二次规划问题的解,即
(2)
问题式(4)、式(5)为凸二次优化问题。
为导出原始问题式(4)、式(5)的对偶问题,引入Lagrange函数进行偏微分,从而得到优化目标的对偶形式,即
(6)

kij=φ(xi)φ(xj)=exp(-‖x-y‖2/g) 。(7)
式中g是核函数参数。
SVM中的惩罚参数C和核函数参数g对算法的计算效率和泛化能力有较大影响,一般情况下人为确定带有一定的盲目性,而且效率很低。所以利用SVM来求解问题的关键是寻找惩罚参数C和核函数中参数g的最优解。关于这2个参数的优化选取,国际上没有公认统一的最好方法,目前采用的方法是在一定范围内取值,通过增加取值范围来获得全局最优解。为了加快搜索速度,本文采用粒子群优化启发式算法对这2个参数进行搜索,寻找最优的SVM参数。
2.1.2 模型参数的粒子群算法优化

图1 PSO算法优化SVM模型流程Fig.1 Flowchart ofPSO-SVM model
Kennedy和Eberhart[11]于1995年提出PSO算法,随后Bratton和Kennedy[12]对PSO算法给出了一个完整的定义。国内许多学者[13-16]将PSO算法运用到边坡位移的预测。主要思想为:在可解空间中定义一群粒子和一个评判其优劣程度的适应度函数,每个粒子反映一个问题的解,粒子适应度大小决定了解的优越性。粒子在解空间中不断地移动,移动速度根据自身和其他粒子的“飞行经验”进行动态调整,粒子移动的方向和距离不断更新,从而需要在解空间中搜索适应度最小值,即问题最优解。其搜索原理为:每个粒子有向2个点逼近的趋势,第一个点是整个种群所有粒子达到适应度最大的位置,即所有粒子在各搜索过程中所达到的全局最优解Gbest;另外一个点是每个粒子达到适应度最大的位置,即个体在各搜索过程中自身所能达到的个体最优解Pbest。通过迭代,更新粒子的位置和速度。PSO算法优化SVM模型的流程如图1所示。
PSO优化算法的数学模型为:假设在一个D维的解空间中,有s个粒子组成的种群,粒子在D维空间中的位置和速度分别为xi={xi1,xi2,…,xiD}和vi={vi1,vi2,…,viD},i=1,2,…,s。首先随机地将各个粒子初始化,然后在每一次迭代过程中动态地跟踪个体极值Pbesti=(pi1,pi2,…,piD)和全局极值Gbesti=(g1,g2,…,gD)。进而更新自身的位置和速度,其更新速度为:
(9)

2.2 Elman神经网络改进SVM预测模型
在SVM预测结果的基础上利用Elman回归的反馈式神经网络[17-19]改进模型。相比于前馈式BP神经网络,Elman神经网络更能描述高度非线性、不确定性和时间相关性的序列的局部瞬变特征,具备时域分辨能力,即能分析后续时序的走势规律。
Elman神经网络的网络结构与传统的BP神经网络相似,其中包含SVM预测误差输入层、隐含层、状态层和SVM-Elman预测误差输出层,网络结构见图2。状态层的作用是记忆隐含层上一次SVM-Elman预测误差的输出值并将其作为下一步预测的输入值。所以说网络在t时刻的输入包含应有的SVM预测误差输入值和隐含层上一次得到的SVM-Elman预测误差输出值2项,同时t时刻的输出能通过递归反馈连接到上下文层单元,并输出到t+1时刻,其中反馈连接的权值不发生改变。连接结构决定回归网络的类型,主要有部分回归和完全回归2种,部分回归有选择地确定反馈连接,本文采用完全回归网络型式。隐含层的数量影响SVM-Elman模型预测的结果,现在普遍的做法是按照经验公式决定隐含层数,这里通过循环的形式寻求最优隐含层数。按照经验公式,本文算例的最佳隐含层数为7,为了加大搜索区间,将隐含层的循环区间取为[0,20],寻找误差最小的隐含层数。

图2 Elman神经网络结构Fig.2 Structure of Elman neural network
设u为r维SVM预测误差输入数据;x为p维中间层结点单元数据;y为q维SVM-Elman预测误差输出结点数据;xc为p维反馈状态数据;w1为承接层到中间层的连接权值;w2为输入层到中间层连接权值;w3为中间层到输出层连接权值;f(*)为中间层神经元的传递函数;g(*)为输出神经元的传递函数,为中间层输出的线性组合,则完全回归的Elman网格描述为:
y(t)=g(w3x(t)) ;
(10)
x(t)=f(w1xc(t))+w2(u(t-1)) ;
(11)
xc(t)=x(t-1) 。
(12)
Elman神经网络的动态映射功能体现在权值修正,权值修正函数的误差表达式为
(13)

3 SVM-Elman模型构建步骤
3.1 预测精度评价指标
实际工程中对边坡位移的时序数据,需要选取一部分作为模型的训练值,其余的部分作为模型预测值,通过比较预测值与实测值之间的误差,可以衡量预测模型的精度,实测值与预测值相差越少,模型预测精度就越高。本文采取实测值与预测值之间的相对误差Err和均方根误差MSE作为评价指标,分析预测模型对边坡位移时序每个数据序列和整体序列预测效果,即有:

(15)

Err越小,表示该数据序列的预测精度较高;MSE越小,表示该预测序列的整体精度较高,预测模型越稳定。
3.2 预测样本数据集的构建

3.3 建立参数优化SVM-Elman模型
惩罚参数C和核函数参数g的选择直接影响SVM-Elman预测模型的精度,SVM-Elman模型的最佳学习样本数d、最佳测试样本数m、Elman神经网络隐含层数h、惩罚参数C和核函数参数g的寻优过程如下所述。
(1)根据监测位移数据,设定d和m的范围,在该范围内选取一组学习样本和测试样本。
(2)设置PSO初始参数。包括粒子维数和个数、搜索区间、加速度因子、惯性权重系数等;确定待优化参数C和g的取值范围,并设置最大速度。
(3)对C和g的任意组合,建立SVM模型并计算适应度函数F(xi),与其自身的最优值F(Pbesti)进行比较,如果F(xi)偏小,即F(xi) (16) 式中:fi为第i个样本的预测值;yi为第i个样本的实测值。 (4)将每个粒子的最优适应度值F(xi)与所有粒子的最优适应度值F(Gbest)相比较,如果F(xi) (5)判断终止条件为:迭代次数T=1 000或适应度值F(xi)<1×10-4,若否,则返回步骤(4)。 (6)记录该d和m组合下SVM模型的最优参数C和g,并滚动预测边坡位移序列。 (7)利用不同隐含层的Elman神经网络对SVM模型预测误差进行预测,得到预测误差最小的隐含层数。 (8)判断终止条件为:循环次数n=20或均方根误差MSE<1×10-4。 (9)返回步骤(1),计算d和m的所有组合。 (10)根据边坡位移序列预测误差最小的d,m,h,C,g建立最终的SVM-Elman模型。 某水电站地处云贵高原,主坝为混凝土面板堆石坝,坝高115 m。工程水文地质条件复杂,长期受风化作用影响,具有节理裂隙发育的岩层,岩体整体性差。左岸强卸荷区高边坡位于坝肩和引水系统进口段,存在失稳的可能性。因此,在该段布置了多点位移计对边坡沉降位移(简称位移)进行实时监控。选取观测点C2-XH-M-01-D3在1 a内的边坡位移实测数据作为预测模型的训练样本,共32个,时间序列即为32;接下来4个月的实测数据作为预测模型的检验样本,共12个,时间序列即为12。原始样本数据集时间间隔约为10 d。 通过试算得到最佳学习样本数为32,最佳测试样本数为12,预测时间步长为1,构造32个训练数据作为初始学习数据集,采用实时滚动预测,即每次预测下一时刻的边坡位移值,然后将新的预测值补充到训练样本中去,并去掉起始时刻的实测值,更新训练样本后重新学习,建立新的预测训练集,继续预测下一次的边坡位移值。在12次预测过程中PSO优化算法初始参数设置为:种群规模为20,参数c1=1.5,c2=1.7;C和g的取值范围分别为[0,100]和[0,1 000];算法停止条件为适应度函数值<10-4,终止迭代步数=1 000。表1列出了32个学习样本的位移实测值、SVM拟合值、绝对误差和相对误差。 表1 位移实测值和SVM预测值比较 时间序列实测值/mmSVM预测值/mm绝对误差/mm相对误差/%1-0.712 -0.731 -0.019 2.67 2-0.721 -0.702 0.019 2.64 3-0.739 -0.720 0.019 2.57 4-0.749 -0.735 0.014 1.87 5-0.749 -0.744 0.005 0.67 6-0.749 -0.675 0.074 9.88 7-0.749 -0.712 0.037 4.94 8-0.749 -0.749 0.000 0.00 9-0.824 -0.824 0.000 0.00 10-0.824 -0.824 0.000 0.00 11-0.787 -0.806 -0.019 2.41 12-0.787 -0.768 0.019 2.41 13-0.787 -0.785 0.002 0.25 14-0.787 -0.795 -0.008 1.02 15-0.824 -0.901 -0.077 9.34 16-1.080 -1.027 0.053 4.91 17-1.194 -1.117 0.077 6.45 18-1.231 -1.299 -0.068 5.52 19-1.636 -1.713 -0.077 4.71 20-1.640 -1.630 0.010 0.61 21-1.660 -1.586 0.074 4.46 22-1.673 -1.677 -0.004 0.24 23-1.709 -1.578 0.131 7.67 24-1.746 -1.658 0.088 5.04 25-2.002 -1.866 0.136 6.79 26-2.075 -1.876 0.199 9.59 27-2.147 -2.127 0.020 0.93 28-2.150 -2.139 0.011 0.51 29-2.220 -2.292 -0.072 3.24 30-2.220 -2.331 -0.111 5.00 31-2.220 -2.344 -0.124 5.59 32-2.256 -2.180 -0.076 3.37 从图3可以看出,该高边坡的变形位移存在较为明显的“台阶式”增长特征,SVM模型对边坡位移监测学习样本的学习率在“台阶”跳跃之前个体的相对误差总体控制在5%以内,在“台阶”跳跃之后个体的相对误差控制在5%~10%,说明SVM模型对高边坡的非线性突变拟合适应性不强。为了得到较为准确和合理的预测结果,利用Elman神经网络对于SVM模型的拟合绝对误差进行学习和预测,并改进了SVM模型。 图3 SVM预测位移、实测位移与时间序列的关系Fig.3 Relationship of SVM-predicted and measureddisplacements against time series 利用Elman神经网络分析实测值和SVM预测值之间绝对误差的后续走势,记忆上一步的误差,并将其反馈给下一次的预测,从而使预测的精度提高。具体而言,运用Elman神经网络训练并预测SVM的绝对误差,然后将预测的绝对误差反馈到SVM预测结果中,SVM-Elman模型的预测结果为SVM模型的预测结果与Elman神经网络预测的绝对误差之和,使SVM预测模型精度提高。预测训练样本的构建与本文4.1节相同,利用SVM-Elman神经网络对第33—第44个时步进行了动态滚动预测。在训练Elman网络中,隐含层数影响所建模型的拟合精度,在循环预测过程之中预测精度在10%以内的隐含层数有4组,分别为7,11,14,18,比较这4组隐含层数的预测结果,分析不同隐含层数对SVM-Elman模型的影响,见表2和图4。 隐含层数为11,14,18时,预测的结果在实测值附近的波动范围较大,难以体现边坡位移的真实发展规律;而隐含层数为7时,预测值与实测值之间的贴合度较高,能较好地反映边坡位移的发展趋势。正确选择隐含层数能直接有效地提高模型的预测精度,本文通过控制预测数据的相对误差和MSE来寻找最佳的隐含层数,最终通过循环计算得到最佳隐含层数也为7层,与经验公式计算的隐含层数一致;传递函数选取双曲正切Sigmoid函数,输出采用Purelin线性函数,每一层的权值和阈值都由最小的随机数组成,网络的学习速率为0.01,学习增率为1.05,学习减率为0.7,动量常数选为0.9。试验表明,上述这一系列参数的选择不但可加快网络收敛速度,而且可提高网络的拟合精度。 表2 不同隐含层数SVM-Elman模型预测位移与实测位移结果比较Table 2 Comparison between predicted displacements of SVM-Elman model with different hidden layersand measured results 图4 不同隐含层预测位移、实测位移与时间序列的关系Fig.4 Relationship of predicted displacements withdifferent hidden layers and measured displacementsagainst time series 表3 SVM模型和SVM-Elman模型预测结果Table 3 Prediction results of SVM model andSVM-Elman model 表4 SVM模型和不同隐含层数SVM-Elman模型预测结果误差Table 4 Prediction results of SVM model andSVM-Elman model with different hidden layers 图5 不同模型预测位移、实测位移与时间序列的关系Fig.5 Relationship of predicted displacement bydifferent models and measured displacementagainst time series 合适隐含层数的SVM-Elman模型具备预测值与实测值吻合度较高、误差较小、精度较高的优点。 由于岩体高边坡变形的影响因素众多,合理预测边坡位移具有一定的复杂性。通过试算得到整个实测序列的最佳学习样本数、最佳测试样本数,然后循环使用经PSO算法优化的SVM模型对实测边坡位移数据进行滚动拟合,得到相应优化的SVM模型优化参数,在此基础上选择合适的Elman神经网络隐含层数,预测高边坡位移绝对误差的总体走势规律,将SVM预测值与Elman神经网络预测的绝对误差值相加,得到SVM-Elman模型预测值,缩小位移时序系列的相对误差,建立SVM-Elman模型。工程实例结果表明,该模型与传统的SVM模型比较,预测稳定性好,预测值与实际相符,预测精度明显提高,能合理有效地预测高边坡位移。4 算例分析
4.1 SVM时序位移拟合
Table 1 Comparison of displacement values betweenmeasurement and SVM prediction

4.2 Elman神经网络改进

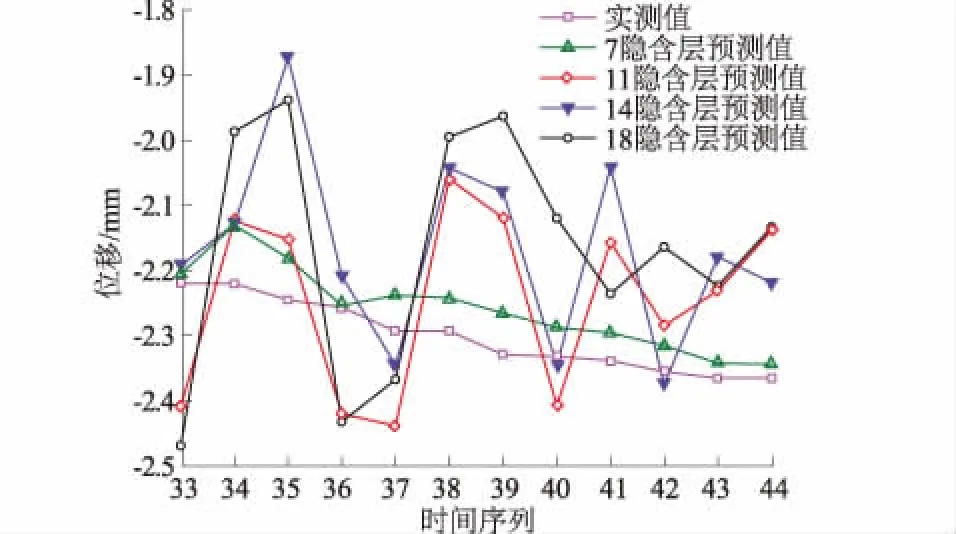
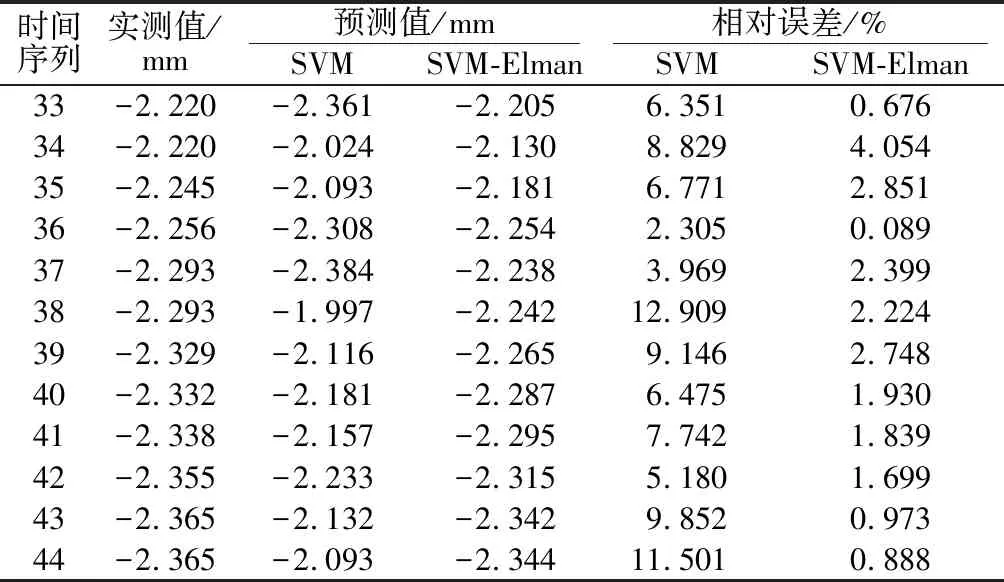
4.3 预测结果的对比分析


5 结 语

