焊接工艺参数对船用高强度钢平板残余应力的影响

谷晓梅1,2， 张晓飞， 宋彦宏

(1.中国船舶重工集团公司 第七一一研究所，上海 201108; 2.江苏科技大学 船舶与海洋工程学院， 江苏 镇江 212003;3.陆军军事交通学院 船艇动力系， 江苏 镇江 212003)

0 引 言

近年来，一些船体结构已逐渐采用高强度钢板焊接而成，在建造过程中，施工人员一般凭借自身的焊接经验或前期进行一系列力学试验保证焊接质量。焊件的加热和冷却不均匀导致焊缝各点的热循环曲线不同，产生焊接残余应力，复杂的应力状况可能降低结构受力性能[1]。若仅依靠人工试验积累测试数据，则需花费大量时间和试验经费。目前，数值模拟方法已成为分析焊接残余应力的重要手段[2-4]。

苍松等[5]以T型焊接接头为例，通过数值仿真分析不同预热温度和不同焊接速度对残余应力的影响，但是并没有进行试验对比。张胜跃等[6]选取12Cr1MoV异质接头作为试验材料，研究焊接电压、焊接电流等焊接工艺参数之间的耦合关系，并通过试验和有限元法对焊接过程进行分析，结果表明焊接电压、焊接电流与焊接残余应力等线性正相关。周方明等[7]研究冷金属过渡(Cold Metal Transfer， CMT)技术平板堆焊焊道间距和焊枪倾角对焊缝成形的影响。AMIN等[8]研究电流、电弧电压、焊接速度和夹角对低碳钢埋弧焊残余应力的影响，结果表明焊接速度和电弧电压对残余应力有显著影响。ALIPOORAMIRABAD等[9]研究两种焊接方法(药芯焊丝和改进型短弧焊组合焊接方法、保护金属电弧焊焊接方法)对高强度低合金钢焊接接头残余应力的影响。

目前关于焊接工艺参数对船用高强度钢平板残余应力影响的研究较少，本文以高强度钢平板对接焊为研究对象，采用试验和数值模拟的方法，分析不同焊接电流和焊接速度对高强度钢对接焊平板残余应力的影响，从而达到改变相关工艺参数降低焊接残余应力的目的。

1 焊接有限元分析相关理论

1.1 焊接温度场有限元分析

焊接件的温度分布是坐标和时间的函数[10]：

T=f(x,y,z,t)(1)

式中：x、y、z为空间坐标；t为时间坐标；T为温度分布函数。

焊接温度场的分析属于典型的非线性瞬态热传导问题[11]，其控制方程为

(2)

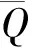
1.2 焊接应力场有限元分析

基于热弹塑性分析方法，采用ANSYS有限元分析软件对焊接残余应力进行数值仿真模拟。

1.2.1 应力-应变关系

由于焊接温度场的存在，焊接件产生一定的弹塑性变形，其应力-应变关系为

dσ=Ddε-CdT(3)

式中：dσ为应力增量；dε为应变增量；D为弹性或弹塑性矩阵；C为与温度有关的向量。

1.2.2 有限元平衡方程

结构某一单元在有限元分析中有如下平衡方程：

dFe+dRe=Kedδe(4)

式中：dFe为单元节点上力的增量；dRe为温度引起的单元初应变等效节点力增量；dδe为节点位移增量；Ke为单元刚度矩阵。

整个构件的平衡方程为

Kdδ=dF(5)

式中：总刚度矩阵K=∑Ke；总载荷向量dF=∑(dFe+dRe)；dδ为各节点位移增量。考虑到焊接过程一般无外力作用，环绕每个节点的单元相应节点的力是自相平衡的力系，即可取∑Fe=0，故有dF=∑dRe。

1.3 热源模型

采用均匀热源模型模拟对接焊接头焊缝可更合理地反应焊接残余应力分布。均匀热源模型即为体热源模型，模拟过程中辅以“生死”单元，以热率载荷的形式加载，其表达式[12]为

(6)

式中：H为生热率；η为电弧有效热效率；U为焊接电压；I为焊接电流；A为焊缝横截面积；v为焊接速度；dt为每载荷步加载时间。

2 高强度钢对接焊平板残余应力数值模拟

图1 平板尺寸

采用ANSYS有限元分析软件中的APDL语言编制对接焊平板残余应力计算程序。

2.1 有限元模型及网格划分

研究对象为船用高强度钢对接平板，由两块尺寸为150 mm×200 mm×6 mm的高强度钢板焊接而成，平板尺寸为300 mm×200 mm×6 mm，如图1所示。焊接方式为单面焊接，焊缝宽度为10 mm。高强度钢材料属性如表1所示。

表1 高强度钢材料参数

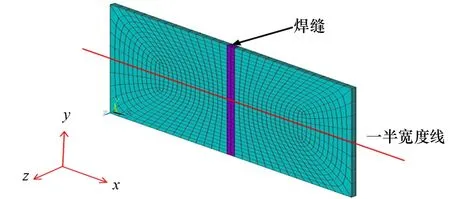
图2 焊接试件有限元模型

以平板长度方向为x轴、宽度方向为y轴、厚度方向为z轴，参照图1尺寸建立有限元模型，如图2所示。为了获得良好的瞬态温度场，参考文献[13]将焊缝区网格尺寸细化，远离焊缝区网格尺寸逐渐增大，既保证计算精度，又减少计算时间。

2.2 边界条件

根据施工工艺情况和条件，在实际焊接时高强度钢平板的四角固定，所以在有限元计算时，限制焊件四角的自由度以确保平板在焊接模拟过程中不会发生刚性位移。定义初始温度和环境温度为20 ℃，并在平板与空气接触的外表面区域施加对流载荷，取对流放热系数为62.5 W/(m2·℃)，以模拟实际焊接过程中平板与周围空气的热对流、热交换过程。

2.3 计算结果

计算在焊接速度为8 cm/min和焊接电流为122 A工艺条件下高强度钢平板的焊接残余应力。由于垂直于焊缝方向的残余应力σx对结构强度有较大影响，取焊件有限元模型一半宽度线上垂直于焊缝方向的残余应力σx绘制分布曲线，如图3所示。从图3可知，垂直于焊缝方向的焊接残余应力σx呈对称单峰形式分布，在焊缝中心线上的残余应力最大，两侧的残余应力急剧减小，在焊趾(即熔合线)部位的残余应力较热影响区略小，热影响区再向外，离焊缝中心线越远，焊接残余应力缓慢减小。

图3 焊缝轴向焊接残余应力σx分布曲线

3 高强度钢对接焊平板残余应力试验

3.1 焊接要求

试验所采用的焊接工艺要求[14]如下：

(1) 焊接过程严格按照《高强度钢焊接基本规则》执行。

(2) 在焊接时，采用手工电弧焊作业。电焊机使用直流电源，接法为反极性，允许电网的波动范围为±15%。

(3) 采用Ф3.2 mm×350 mm的J507碳钢焊条进行焊接。

(4) 在焊接过程中，保持匀速焊接，确保焊接的线能量不大于19 kJ/cm，记录每块焊接试件的焊接电压、电流和焊接速度数据。

按照焊接要求，将6块尺寸均为150 mm×200 mm×6 mm的焊接试板每两块焊接成1块尺寸为300 mm×200 mm×6 mm的平板试件，分别命名为A板、B板、C板，焊接电压为23 V，焊接电流为122～124 A，焊接速度为7.8～8.7 cm/min，环境温度为20 ℃。焊接后的试件如图4所示。每块试件的焊接工艺参数如表2所示。

图4 焊接试件及焊接工艺参数

焊接工艺参数A板B板C板焊接电流I/A124122122焊接电压U/V232323焊接时间t/s147154138

3.2 焊接残余应力测量

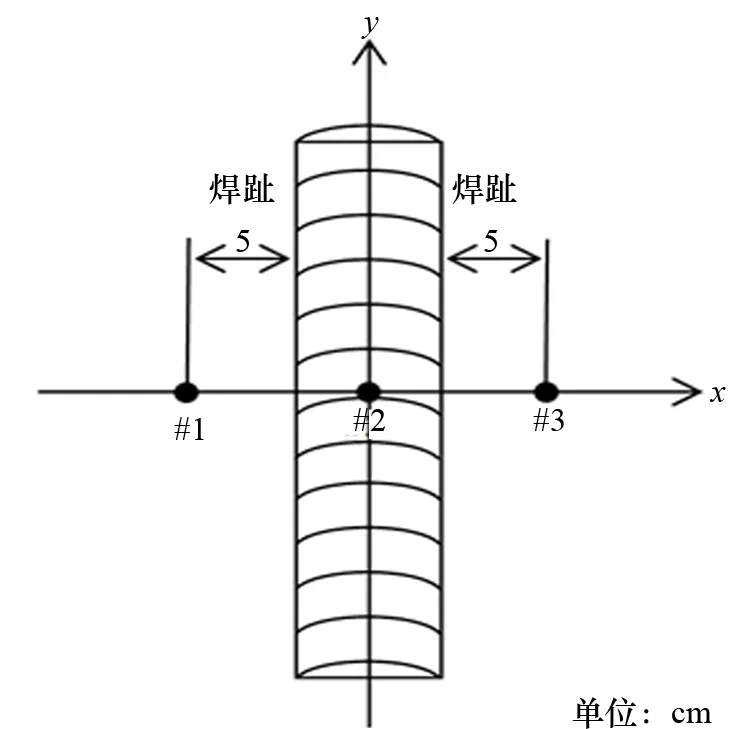
图5 测点位置图

有损检测焊接残余应力测量方法是利用机械加工或其他方法将被测件一部分去除，造成部分或全部残余应力释放，测定相应的位移、裂纹和应变等量值，并通过力学分析和计算，推算被测件原始存在的残余应力。为便于测量，大多数有损检测选定应变作为测量参数。有损检测法主要包括盲孔法、环芯法、剥层法、剖面法和裂纹法等。

图6 试板应变花布置图

盲孔法是目前较为成熟的方法，其基本思路是在具有残余应力的构件上钻1个小孔，使孔的邻域内由于部分应力释放而产生相应的位移和应变，经相关公式换算后得到钻孔处原有的残余应力。

采用盲孔法对试件垂直于焊缝方向的轴向残余应力σx进行测量，步骤如下：

(1) 选取如图4所示的3块高强度钢平板试件焊缝中心线处和距焊缝中心线±5 cm处的3个点作为测量点，分别命名为测点#1、#2、#3，测点位置如图5所示。

(2) 打磨并用丙酮或酒精清洗测量点表面，在测点位置贴上如图6所示的应变花，在应变花中心打1个直径约2 mm、深约2.5 mm的小盲孔引起残余应力释放。

(3) 采用济南西格玛公司生产的ASMC1-9应变测量仪测得释放量并通过计算得到3个测点位置的残余应力大小。

(4) 将每个测点测量结果取平均值作为最终测量结果，如表3所示。

表3 焊接试件轴向残余应力平均值

3.3 试验结果与数值模拟结果对比

将第3.2节测量结果与第2.3节焊接数值模拟结果进行对比验证，如图7所示。从图7可知，测量数据与数值模拟结果基本一致，表明数值模拟的合理性，并且可满足接下来的分析要求。因此，应用本文有限元分析方法进行高强度钢焊接数值模拟研究是可行的。

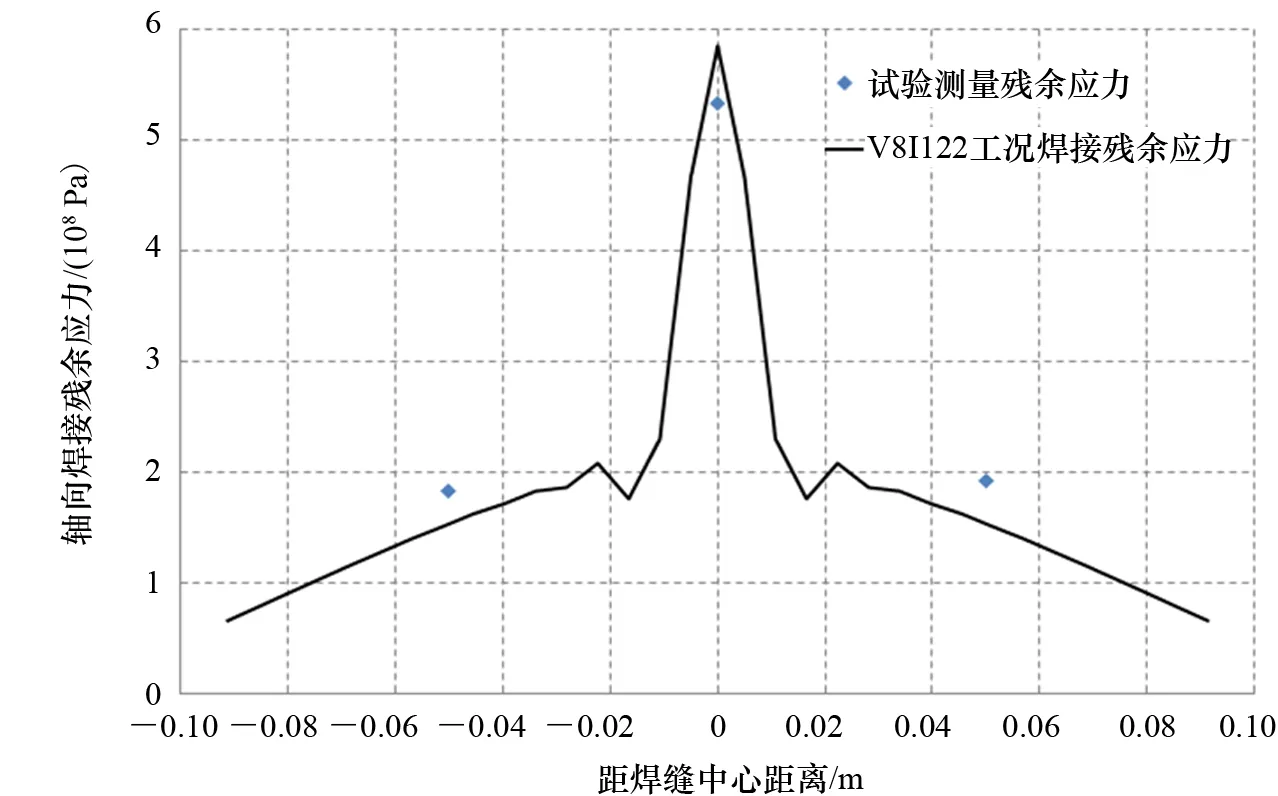
图7 测量值与模拟计算结果对比

4 焊接工艺参数对高强度钢对接焊平板残余应力影响

4.1 研究工况

以某船厂高强度钢焊接工艺参数范围为参照，分别将8 cm/min、10 cm/min、12 cm/min等3种不同焊接速度和100 A、110 A、120 A、130 A等4种不同焊接电流进行自由组合，得出如表4所示的12种工况，分别对这12种工况进行焊接数值模拟，并将计算结果进行比较。

表4 12种焊接工况组合形式

4.2 不同焊接电流对高强度钢对接焊平板残余应力影响

在其他条件不变的前提下，仅改变焊接电流，使焊接线能量产生差异，进而影响焊接残余应力的产生和分布。对比分析焊接速度值一定、焊接电流不同的3组工况下数值模拟计算结果，研究焊接电流对高强度钢平板对接焊焊接残余应力的影响程度。

当焊接速度为8 cm/min时，不同焊接电流情况下焊接残余应力对比如图8所示。当焊接速度为10 cm/min和12 cm/min时，不同焊接电流情况下焊接残余应力对比图与焊接速度为8 cm/min时分布规律基本相同，均呈对称单峰分布，仅最大值有所变化。不同焊接速度下各工况残余应力最大值如表5所示。

图8 V8工况焊缝轴向焊接残余应力分布对比图

表5 12种焊接工况轴向残余应力最大值 MPa

将表4和表5中V8(V8I100、V8I110、V8I120、V8I130)、V10(V10I100、V10I110、V10I120、V10I130)、V12(V12I100、V12I110、V12I120、V12I130)等3组工况下的轴向焊接残余应力最大值采用回归分析法，用多项式进行拟合，形成拟合曲线如图9所示。通过对比可知：增大焊接电流，焊接残余应力最大值随之增大；当焊接电流升高至一定程度后，残余应力最大值的增大趋势逐渐减缓。

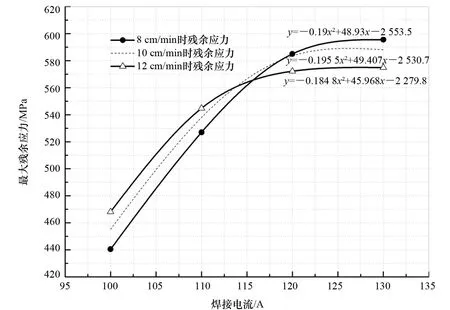
图9 不同焊接电流对平板最大残余应力的影响

4.3 不同焊接速度对高强度钢对接焊平板残余应力的影响

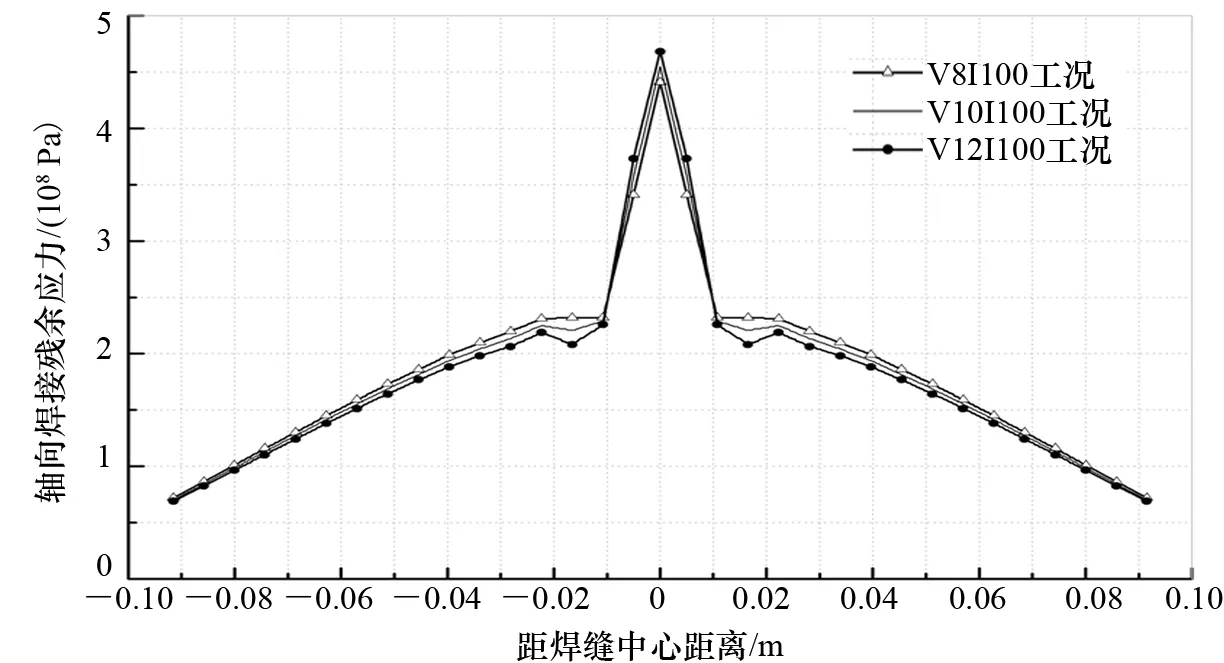
图10 I100工况焊缝轴向焊接残余应力分布对比图

在其他条件不变的前提下，仅采用不同焊接速度进行焊接模拟，使焊接线能量产生差异，从而影响焊接残余应力的产生和分布。将12种工况分成焊接电流为100 A、110 A、120 A、130 A的4组，研究不同焊接速度对高强度钢平板对接焊焊接残余应力的影响程度。

当焊接电流为100 A时，不同焊接速度的焊接残余应力计算结果如图10所示。当焊接电流为110 A、120 A、130 A时，不同焊接速度的焊接残余应力计算结果与焊接电流为100 A时分布规律基本相同，均呈对称单峰分布，仅最大值有所变化。

将表4和表5中100 A(V8I100、V10I100、V12I100)、110 A(V8I110、V10I110、V12I110)、120 A(V8I120、V10I120、V12I120)、130 A(V8I130、V10I130、V12I130)等4组工况下的焊接残余应力最大值采用回归分析法，用多项式进行拟合，形成拟合曲线如图11所示。通过对比可知：当焊接速度逐渐加快，焊接电流在100～110 A时，焊接残余应力最大值随之增大；但焊接电流在120～130 A时，焊接残余应力最大值逐渐变小。

图11 不同焊接速度对平板最大残余应力的影响

焊接应力是由焊接过程中不均匀加热导致的，因此焊接热输入是影响焊接残余应力的关键因素。通常1条焊缝施焊处受热发生膨胀变形，最高温度可达到材料的沸点，随后在凝固冷却时发生收缩，热源附近金属形成的温度场的温度梯度较大，其形成的主要原因是焊接热输入[15]。

通常来讲，热输入的差异主要由焊接电流和焊接速度引起。当焊接电流较小时，焊接热输入整体较小，焊接速度越大，焊接温度场梯度变化越大，焊件受热不均匀现象越严重，焊接残余应力值越大，如图11焊接电流在100 A和110 A工况所示。当焊接电流较大时，焊接热输入明显增大，虽然焊接速度也增大，但从整体看，温度梯度的变化减缓，即焊件受热相对均匀，焊接残余应力反而逐渐减小，如图11焊接电流在120 A和130 A工况所示。

5 结 论

以高强度钢平板对接焊为研究对象，采用数值模拟和试验验证的方法，对比分析在不同焊接电流和焊接速度值时高强度钢平板对接焊的残余应力分布，主要结论如下：

(1) 在焊接方法、焊接速度及其他条件相同的前提下，升高焊接电流，垂直于焊缝方向的残余应力分布曲线形状近似相同。焊接残余应力最大值随电流升高而增大，当焊接电流升高至一定值后，残余应力最大值随电流升高而增大的趋势逐渐减缓。

(2) 在焊接方法、焊接电流及其他条件相同的前提下，增大焊接速度，垂直于焊缝方向的残余应力分布曲线形状也近似相同。当焊接速度逐渐增大，焊接电流在100～110 A时，焊接残余应力最大值随之增大；然而当焊接电流在120～130 A时，焊接残余应力最大值逐渐变小，但其值还是远大于焊接电流在100～110 A时的焊接残余应力。

(3) 由于焊接速度为8 cm/min、焊接电流为100 A时焊缝的焊接残余应力为所有工况中最小的，从减小焊接残余应力的角度出发，建议焊接速度8 cm/min、焊接电流100 A为高强度钢平板对接焊时的最佳参数。