含腐蚀缺陷的顶张式立管局部屈曲特性
余 杨 余建星 徐立新 陈柏全
(1. 天津大学 水利工程仿真与安全国家重点实验室, 天津 300350;2. 高新船舶与深海开发装备协同创新中心, 上海 200240)
0 引 言
近年来,全球经济的迅速发展加速世界各国对能源的需求,当前世界各国主要通过海上浮式结构平台以及附属结构装备和系统实现深海丰富油气资源的开采[1]。立管已成为链接海底开采设备和海上各种结构物的必不可少的纽带。
腐蚀是顶张式立管破坏的主要因素之一,实际调查发现立管因腐蚀会形成多种深度和不规则形状的腐蚀缺陷坑群[2]。含腐蚀缺陷的立管在腐蚀管段部分壁厚会变薄,在复杂的环境载荷作用下立管很容易发生屈曲失效,造成环境污染和经济损失。对顶张式立管局部屈曲特性进行研究是确保立管安全运行的前提。
针对含腐蚀缺陷管道的抗屈曲性能问题,国内外许多学者进行了研究。在国外:IFLEFEL等[3]通过数值模拟研究含有缺陷的海底管带在弯矩作用下的屈曲过程; HAUCH等[4]研究完好管道破坏机理并深入到腐蚀管道的研究;ALVES等[5]采用三维有限元方法分析腐蚀管道在联合荷载作用下的破坏形式;美国机械工程师协会(ASME)制定了B31G规范对含有腐蚀的海底管道进行评估[6-7],但是结果具有保守性和局限性。在国内:余建星等[8]在天津大学自主研制开发全尺寸试验装置——深海压力舱,用以模拟深海油气运输管道所处环境,并以此为依托,综合考虑管道的腐蚀缺陷、初始椭圆度和壁厚比等这些敏感性因素,设计全尺寸管道压溃试验方案;陈宏远等[9]采用弹塑性有限元法结合非线性屈曲理论,分析受初始缺陷影响(管径不均和壁厚不均)的管线管在外压作用下的非线性屈曲。
国内外已经针对含初始缺陷的海底管道从理论和试验方面开展了相关研究。由于顶张式立管是内层油管加外层套管的管中管结构,在实际工况中受轴向张力和外壁水压的复杂载荷作用,针对含腐蚀缺陷的顶张式立管局部屈曲特性的研究,在国内外发表的文献资料中鲜有报道。本文针对含有腐蚀缺陷的顶张式立管,建立外层管全局腐蚀和局部腐蚀两种腐蚀缺陷形式,对其压溃因数和腐蚀参数变化的规律进行敏感性分析和相关性分析。
1 腐蚀缺陷描述
腐蚀是顶张式立管破坏的主要因素之一。在作业过程中,外部海水的冲刷腐蚀导致顶张式立管外层部分管段厚度不均匀,这些腐蚀缺陷会进一步加剧顶张式立管的屈曲失效,直接影响立管的局部应变、剩余强度和疲劳寿命,给系统安全运行带来潜在危害。

图1 全局腐蚀 图2 局部腐蚀
根据腐蚀区域大小将腐蚀形式理想化为局部腐蚀和全局腐蚀。全局腐蚀指沿整个外层立管的长度方向都存在腐蚀作用,用以模拟腐蚀缺陷发生在立管表面的全部或者大部分区域,如图1所示。局部腐蚀是指在立管局部存在槽型腐蚀区域,用以模拟外层立管表面较小区域内发生腐蚀缺陷,如图2所示。
2 有限元模型
2.1 建模流程
2.1.1 几何模型
顶张式立管模型为管中管结构,外管外径为273.1 mm,壁厚为10.16 mm,内管外径为139.7 mm,壁厚为7.72 mm,管长为8 m。生产精度不高导致在立管的横截面处存在不圆度,设置立管中间剖面初始椭圆度为0.5%(内管和外管均有初始椭圆度)。由于顶张式立管的对称性及其所受的复杂载荷,选取结构1/2部分作为有限元模型,并且在外层立管中间位置环向切除一部分槽型区域模拟腐蚀缺陷(深度、宽度、长度按照不同的腐蚀参数进行选取)。
顶张式立管采用API X65型钢材,外管与内管的材料属性如表1所示。

表1 顶张式立管(内管和外管)材料属性
采用Romberg-Osgood方程建立本构关系,方程的基本形式为
(1)
式中:ε为应变;σ为应力;E为弹性模量;σy为极限抗拉强度;n为应变硬化指数。
进行材料的轴向拉伸试验验证R-O方程的正确性,根据表1的参数和试验测得的数据绘得如图3所示曲线。
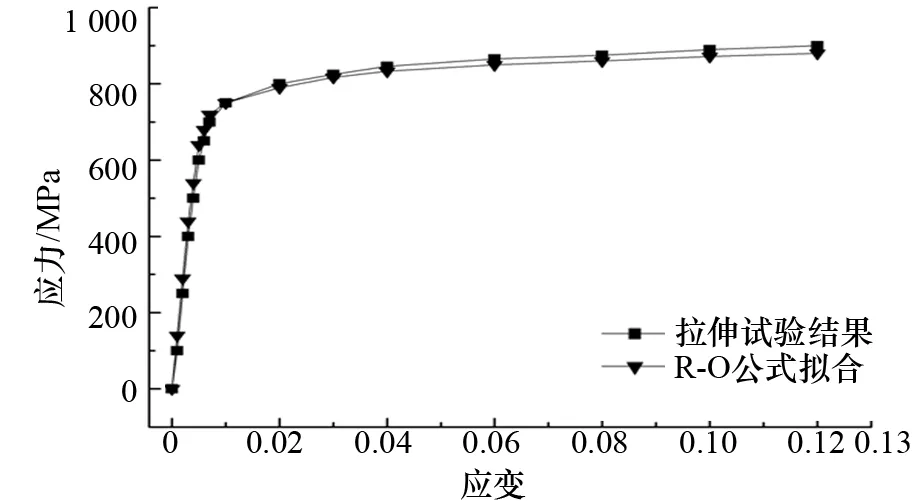
图3 拉伸试验结果与R-O公式计算结果对比
2.1.2 网格划分
选择8节点六面体线性减缩积分单元(C3D8R单元),采用在模型边上布种的方法对管道进行网格划分,在轴向、径向和环向上布种,并对腐蚀缺陷附近立管进行网格加密。

图4 局部腐蚀立管屈曲应力云图
2.1.3 接触和摩擦
将外层立管的内壁设置为从面,内层立管的外壁设置为主面。外管内侧与内管外侧为面面接触,切向无摩擦,法向硬接触,不能穿透,内管内侧为自接触。
2.1.4 约束和载荷
在管道模型对称面上施加对称约束,上端约束条件为固支约束,下端允许轴向位移。立管顶部一般通过张紧器与平台连接,底部通过应力接头与海底设备连接,因此立管一端受轴力,外壁受静水压力作用。
2.2 分析过程
通过在顶张式立管管端施加轴力、外壁施加面载荷模拟立管实际受压过程,立管的压溃过程如下:含有初始缺陷的腐蚀立管在受外压作用时,腐蚀附近立管受到较大应力首先发生变形;之后立管在外压作用下,沿立管存在腐蚀缺陷的方向发生变形,此时腐蚀处以及两侧所受应力较大;最后立管在存在缺陷的截面压溃,沿管长方向发生屈曲传播。如图4所示。
3 结果对比与分析

图 5 腐蚀参数几何形状
3.1 腐蚀参数选取
腐蚀缺陷的尺寸对含有腐蚀顶张式立管结构的压溃载荷有极大影响。本文主要讨论缺陷长度、深度和宽度对压溃载荷的影响,通过无量纲参数表示腐蚀缺陷尺寸的变化,用θ/π表示腐蚀宽度,用d/t表示腐蚀深度,用L/L0表示腐蚀长度参数,t为外层立管壁厚,L0为立管长度。腐蚀参数几何意义如图5所示,其中θ为沿截面腐蚀区域的圆心角度,d为腐蚀区域绝对深度。全局腐蚀和局部腐蚀参数具体取值如表2所示。
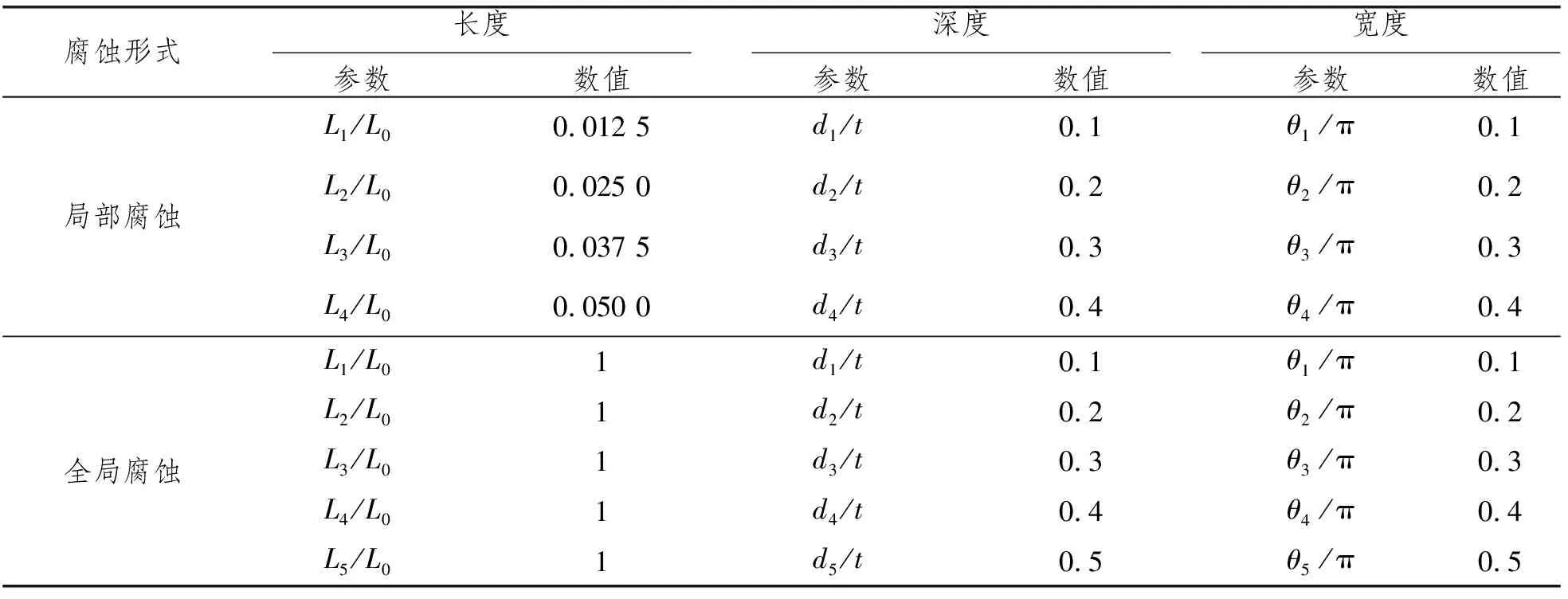
表2 腐蚀缺陷无量纲参数
3.2 单层立管与双层顶张式立管对比
对于顶张式立管,需考虑单层立管结构的工况,其受力情况和约束条件与双层顶张式立管相同。单层立管尺寸如下:管道外径为273.1 mm,壁厚为10.16 mm,管长为8 m,在立管中间截面存在0.5%的初始椭圆度。
选取两组全局腐蚀形式的顶张式立管(均为外层管腐蚀),利用ABAQUS建立单层立管和双层立管模型进行屈曲特性分析,腐蚀参数选取与计算结果如表3所示。

表3 单层管与双层管对比结果
由表3数据可知:腐蚀深度d/t=0.4、腐蚀宽度θ/π=0.4的单层立管压溃压力值较同样腐蚀缺陷的双层立管减小1.35%;腐蚀深度d/t=0.6、腐蚀宽度θ/π=0.4的单层立管压溃压力较同样缺陷的双层立管减小2.95%。
对于顶张式立管这种受复杂载荷的管中管结构,内管和外管共同承担端部的轴力作用,因此单层管的压溃压力小于在相同工况下的双层管的压溃压力,但减小的幅度较小。
3.3 腐蚀参数敏感性
3.3.1 全局腐蚀参数敏感性
对顶张式立管的压溃压力进行无量纲化处理,即引入压溃因数Cf。压溃因数表示顶张式立管因外层立管存在腐蚀缺陷而带来压溃压力的折损,其定义式为
(2)
式中:Pc为含腐蚀缺陷顶张式立管(含初始椭圆度)的压溃压力,N/mm2;Pc0为仅含初始椭圆度顶张式立管的压溃压力,N/mm2。
按照表2腐蚀参数进行组合,给定顶张式立管的初始椭圆度参数为0.5%。压溃因数随不同腐蚀参数的变化规律如图6和图7所示。

图6 腐蚀宽度对Cf的影响 图7 腐蚀深度对Cf的影响
分析图6和图7的变化趋势可知:(1)随腐蚀宽度参数的增加,压溃因数逐渐降低,但是减小的幅值较小。当腐蚀宽度参数大于0.2后,可认为随腐蚀宽度的增加,压溃因数没有明显的变化;当腐蚀深度较深时,缺陷部分发生塑性形变,生成塑性铰,从而产生局部失效。(2)随着腐蚀深度参数的增加,压溃因数逐渐减小。腐蚀深度小,压溃因数减小的幅度小;当腐蚀深度大于0.3后,压溃因数呈线性减小,立管在腐蚀区域发生局部泄漏失效。
3.3.2 局部腐蚀参数敏感性
按照表2腐蚀参数进行组合,给定顶张式立管的初始椭圆度参数为0.5%。压溃因数随不同局部腐蚀参数、长度以及宽度的变化规律如图8~图10所示。

图8 局部腐蚀深度对Cf的影响 图9 局部腐蚀长度对Cf的影响 图10 局部腐蚀宽度对Cf的影响
分析图8~图10的变化趋势可知:(1)随腐蚀深度参数的增加,压溃因数逐渐减小。当腐蚀长度与腐蚀宽度组成的区域面积较小时,压溃因数对腐蚀深度敏感性较强;当腐蚀长度与腐蚀宽度组成的区域面积较大时,压溃因数对腐蚀深度敏感性变弱。(2)随腐蚀长度参数的增加,压溃因数逐渐减小。当腐蚀缺陷在立管横截面上的投影面积较小时,随腐蚀长度的增加,压溃因数没有明显的减小,对于本组模型而言最大减小幅值小于 3%。(3)随腐蚀宽度参数的增加,压溃因数逐渐降低。当腐蚀宽度参数大于0.2时,压溃因数随腐蚀宽度参数的变化不明显。
3.4 腐蚀参数相关性
通过敏感性分析定性地得出腐蚀参数与压溃因数之间存在密切的关系。对于不同的腐蚀形式,每个腐蚀参数与压溃因数的相关性强弱还需进一步通过相关性分析来定量探究。
3.4.1 Pearson相关系数法
Pearson相关系数又叫Pearson积矩相关系数[10],是一种统计学参数,一般用来定量地衡量变量之间的相关关系。若随机变量X、Y的联合分布是二维正态分布,xi和yi分别为n次独立观测值,则计算r的公式为
(3)

Pearson相关系数r有如下性质:r绝对值越接近1,表明两个变量之间的相关程度越强;当相关系数大于 0 时,表示为正相关; 当相关系数小于 0 时,表示为负相关。
利用SPSS数值计算软件,对腐蚀参数X与压溃因数Y进行线性相关性分析,检验样本数据的正态分布性,结果如表4所示。

表4 正态分布检验
一般偏度和峰度这两个参数的绝对值小于1,就可以认为该数据符合正态分布。该研究的压溃因数数据符合正态分布。
3.4.2 腐蚀参数与压溃因数相关性
基于Pearson相关性原理,对两种腐蚀形式的腐蚀参数与压溃因数进行相关性分析,计算结果如表5所示。

表5 不同腐蚀深度、宽度、长度的Pearson相关系数分析结果
分析表5可得:对于含有全局腐蚀的顶张式立管,腐蚀深度参数与压溃因数的 Pearson 相关系数为-0.957,两者为强负相关。腐蚀宽度参数与压溃因数之间的 Pearson 相关系数为-0.149,两者为弱负相关。对于含有局部腐蚀的顶张式立管,压溃因数与腐蚀深度参数、腐蚀长度参数以及腐蚀宽度参数的Pearson 相关性系数分别为-0.744、-0.484、-0.174。由此可见,腐蚀因数与腐蚀参数均为负相关,且腐蚀因数与腐蚀深度参数相关性最强,长度参数其次,宽度参数最弱。
结果表明:对于不同的腐蚀缺陷形式,随着腐蚀参数增加,压溃因数均减小;腐蚀深度、腐蚀长度对压溃因数的影响远大于腐蚀宽度对压溃因数的影响。
4 结 论
采用非线性有限元分析软件ABAQUS建立顶张式立管局部模型,模拟含全局腐蚀和局部腐蚀两种缺陷形式的顶张式立管在复杂载荷作用下的压溃过程,并对压溃因数与腐蚀参数进行敏感性分析和相关性分析,得到以下结论:
(1) 含有全局腐蚀的顶张式立管,压溃因数对腐蚀深度参数敏感性较强,对腐蚀宽度参数敏感性较弱。压溃因数与腐蚀深度和腐蚀宽度均呈负相关,且相关性依次减弱。
(2) 含有局部腐蚀的顶张式立管,压溃因数对腐蚀深度、腐蚀长度的敏感性较强,对腐蚀宽度的敏感性弱。压溃因数与腐蚀深度、腐蚀长度和腐蚀宽度均呈负相关,且相关性依次减弱。
(3) 因为顶张式立管的内管和外管共同承担端部轴力作用,所以在同样的约束和载荷条件下,单层立管的压溃因数小于双层立管,但是相差不明显。

