基于主成分Logistic回归的食品供应链风险预警分析
徐 磊 朱 科 彭金栓
(重庆交通大学交通运输学院,重庆 400074)
食品作为大众日常消费必需品,其供应链的稳定性在社会经济发展中显得尤为重要,但近年来出现的“三鹿奶粉事件”“苏丹红事件”“瘦肉精事件”等重大食品安全事件,说明食品供应链管理存在漏洞。食品安全问题不仅会影响企业的信誉,而且使产品形象在消费者心中发生颠覆,甚至还会造成整个供应链的崩塌。通过研究发现供应链风险预警环节的薄弱是导致问题食品得以在市场上流通而使整个供应链蒙受损失的一个重要原因。有效地对食品供应链风险进行预警分析,能够帮助供应链管理者准确识别与判断供应链所面临的风险,进而制定出相应的风险控制措施,控制风险在供应链上的扩散。
如何快速准确地对食品供应链风险进行预警是急需解决的问题。目前,国内外相关研究大多集中在食品供应链安全管理体系研究、食品供应链优化分析以及供应链风险的模糊综合评判方面[1-2]。王云[3]对食品供应链的配送环节中存在的风险进行了研究,分别建立集中决策与分散决策的Stackelberg模型,以探讨生鲜食品配送风险问题。顾小林[4]从数据挖掘视角甄别出导致食品安全问题的因素,建立了基于关联规则挖掘的食品安全信息预警模型进行安全预警研究。韩景丰等[5]提出在基于危害分析的关键点控制的可追溯性系统中对供应链风险预警过程进行研究。本文依据主成分分析和Logistic回归分析法[6]建立食品供应链风险预警模型,从食品供应链风险种类的划分为出发点,归类不同的风险指标要素,计算出不同风险源的主成分,以风险指标作为Logistic回归变量,以此对食品供应链进行风险预警。以其为食品供应链的稳定发展提供方法参考和理论支持。
以风险指标进行主成分分析,并选取有代表性的主成分对食品供应链风险进行预警。通过对大量实际案例的整理,根据对食品供应链的实证分析以及综合归纳现有研究,总结出食品供应链风险种类的主要指标体系,该指标体系由4大类别风险及12个风险指标组成(见表1)。
根据风险致因理论,食品供应链风险可分为四类:(1)供应风险,由突发事件而导致的供应链供应的中断。(2)生产风险,是指供应链运作中管理不当、机器设备出现故障、生产技术未达到合格标准等原因造成的风险。(3)流通风险,是指流通机制设计或运行中存在缺陷而导致的风险。(4)销售风险,是指在供应链末端发生变化而造成的风险。
1 构建指标体系

表1 食品供应链风险指标体系
2 建立模型
食品供应链风险预警模型可按如下步骤建立:
步骤1:计算主成分特征值和特征向量。
选取n组观测数据,通过正交变换,计算其相关矩阵R的n个特征值以及特征值所对应的特征向量λ1,λ2,…,λn以及特征值λj所对应的特征向量
步骤2:确定主成分个数并选取主成分。
≥85%且特征值大于1的前p个主成分,主成分F1,F2,…,Fp,主成分:

式中,t1,t2,…,tn为标准化指标变量,u1j,u2j,…,unj为特征向量。根据公式(1)计算出p个主成分,用这p个主成分进行Logistic回归分析。
步骤3:选取分析样本。
建立样本矩阵(xi1,xi2,…,xip; yi)(i=1,2,…,n),其中,y1,y2,…,yn是取值为0-1型变量,0表述该食品企业供应链的风险较小,1表述风险较大,xi1,xi2,…,xip是p个主成分组成的新矩阵,yi与xi1,xi2,…,xip的关系为:

步骤4:建立Logistic回归模型。
函数f(x)是值域在[0,1]区间内的单调增函数,对于Logistic回归,有:

将(2)式代人(3)式得Logistic回归模型:

步骤5:计算似然函数。
y1,y2,…,yn的似然函数为:
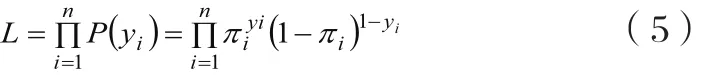
对似然函数取自然对数,得:

对于Logistic回归,将(4)式代人(6)式得:
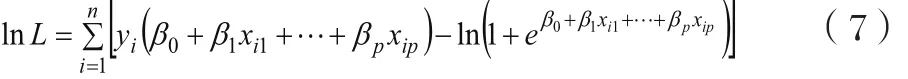
步骤6 :选取β0,β1,…,βp的估计值。
令xi0=1,代入(7)则:

为了求(10)式的极大值,根据迭代公式

设初始值B0=β0,β1,…,βp经过式(10)的迭代,当|Bi+1-Bi|<ε(ε为自设定误差值)时,停止迭代,得到的Bi+1即为所求的B0=β0,β1,…,βp估计值。利用估计值计算出食品供应链风险大小的概率,预测是否会发生高风险事件。
3 实例分析
选取40家食品企业对其供应链风险进行调查。按表1所示风险指标对企业风险大小进行打分,分值范围为0~100。对40个样本指标进行主成分分析和Logistic回归分析,随机抽取20个样本数据作为估计样本产生预警模型,其余数据留作检验样本对模型进行检验。
使用SPSS对样本数据进行主成分分析,各主成分贡献率和累计贡献率如表2所示。由表2可见,前4个主成分方差累计贡献率已超过85%,故引入4个主成分,这4个主成分的特征向量如表3所示。
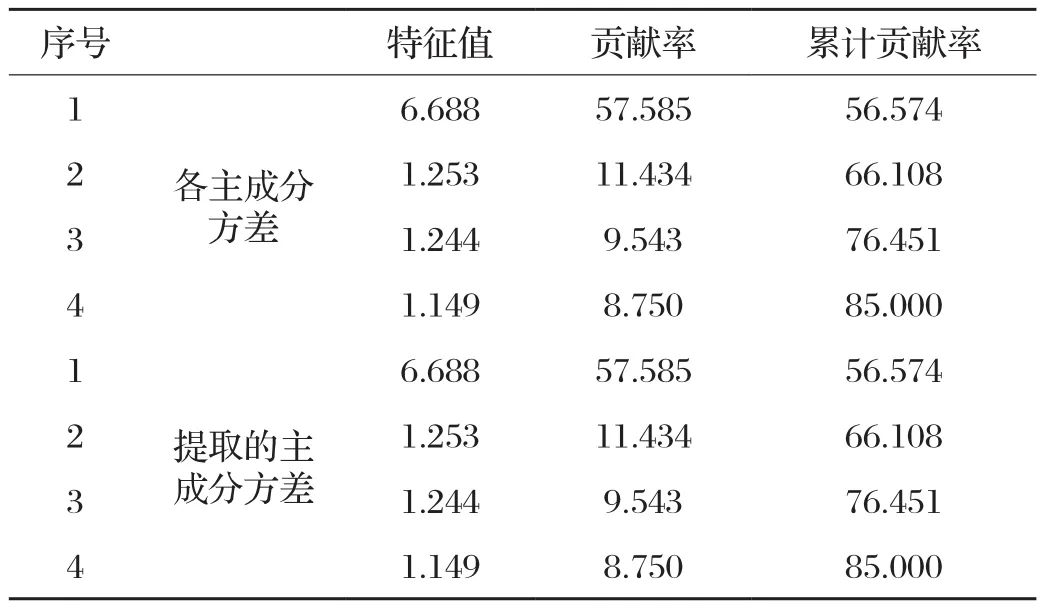
表2 方差及对应的贡献率/%
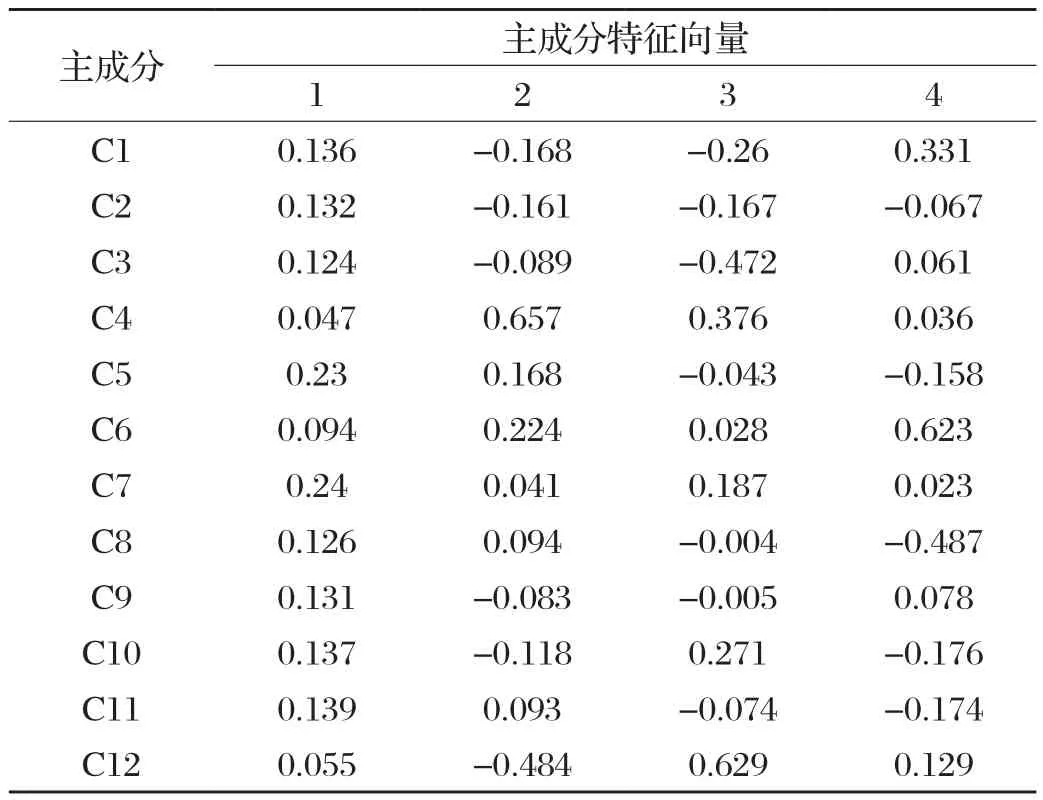
表3 主成分特征向量
根据公式(1)计算出4个主成分F1,F2,F3和F4的值:

将主成分的值作为Logistic预警模型的输入,利用SPSS对由主成分组成的估计样本进行分析,表4显示出变量的选择,可以看出第一主成分P值(显著性)是0.042,常数项的P值为0.035,都小于0.05的检验标准,因此,方程可以通过检验。

表4 方程中的变量

表5 分类预测趋势
表5反映了对应的分类预测情况,模型预测的准确率达到了90%。最终拟合出风险预警模型,由表4可以得到Logistic预测概率模型为:
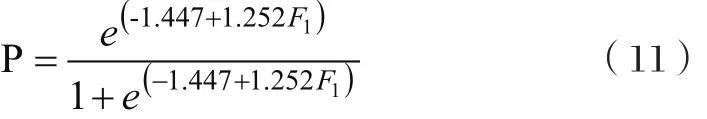
本文所选Logistic回归模型以0.5作为分割点,当P>0.5时,就判定为高风险;当P<0.5时,就判定为低风险。这样就可以用此概率模型进行预警。为了对模型的预警能力和稳健性进行检验,利用随机挑选20家企业作为检验样本对模型进行验证,结果如表6所示。

表6 试验样本预测效果
从上面的结果看,预警的准确率达到了85%,准确率比较高,说明该方法具有较好的适用性和推广性。
4 结语
以第1主成分代表的风险指标具有较强的概括性,基本上可以较好地反映原始指标的信息。综合以上所有结果,以主成分代表食品企业供应链风险指标作为Logistic回归变量,可以很快地预测出企业的风险情况,具有较高的准确性。

