基于权马尔科夫链模型淮北平原西部地下水埋深预测研究

刘海

容之一;地下水位变化受气象、水文、地质、开采及补给等诸多因素制约，而且各因素之间的关系很难确定，难以用简单的线性函数进行描述，故地下水埋深具有随机性。该研究采用基于权马尔科夫链建立淮北平原西部地下水埋深预测模型，预测了区内地下水埋深所处的区间值，结果表明研究区中深层地下水多处于[5.080m，5.960m），处于[6.448m，+∞）出现的概率也偏高;浅层地下水埋深多处于[2.925m，3.635m），处于[3.990m，+∞）也呈现增大趋势，研究表明在地下水不合理的开发利用下，淮北平原西部地下水埋深呈增大趋势;该研究成果为淮北平原西部地下水资源管理与决策提供一种新的方法。

关键词淮北平原;马儿科夫链;预测;地下水埋深

中图分类号S273.4文献标识码A

文章编号0517-6611（2019）01-0068-06

doi：10.3969/j.issn.0517-6611.2019.01.022

开放科学（资源服务）标识码（OSID）：

地下水位埋深动态预测研究是地下水资源评价的重要内容之一，但因受自然地理、地质构造、含水介质、降雨、开采、蒸发等多种因素的影响，使得地下水位埋深动态变化在时序上常表现出复杂的非线性特征[1-3]，对其进行预测一直是学者研究的热点问题之一。目前地下水位埋深的预测模型方法众多，可划分为确定性模型和随机模型两大类。张忠永等[4]利用神经网络方法，根据地下水动态的时间序列数据，建立地下水动态模型，对地下水动态进行模拟和预测;付强等[5]利用回归分析、傅里叶级数谐波分析及自回归模型叠加拟合，提出了一种非平稳时序地下水埋深预测模型;高黎明等[6]将灰色理论模型用于地下水埋深预测;杨忠平等[7]运用时间序列分析理论对地下水位动态变化进行了分析和预报;王新民等[8]采用基于指数预测法、灰色预测法以及线性回归预测法的变权组合预测方法进行水位埋深的模拟和预测;喻黎明等[9]建立基于极限学习机（Extremelearningmachine，ELM）的地下水位埋深时空分布预测模型;此外，还有有限分析法、概率统计法等。不同的方法侧重点各不相同，均取得较好的成果。

马尔科夫理论由俄国数学家马尔科夫（Markov）于20世纪初最初提出，其理论认为一些事物的变化与其近期状态关系极大，而与其远期状态关系很小，甚至可以忽略不计，这种现象被称为“无后效性”。具有无后效性的随机过程称为马尔可夫过程，而時间和状态均离散的马尔可夫过程称为马尔可夫链，随着该理论的不断发展和完善，目前马尔可夫链在降水径流预测[10-13]、水质研究[14-15]、土地利用[16-17]、公路客运量[18-19]、地质灾害预测及地层岩性方面[20-22]得到广泛的应用;马尔可夫链在地下水动态预测方面也有相关研究，如宋印胜[23]运用马尔可夫链模型对鲁南地区未来地下水水位进行状态范围预测;李彬等[24]运用随机理论，建立了基于加权马尔科夫链的河套灌区地下水埋深预测模型。

安徽省淮北平原西部地下水主要受大气降水、河流侧向补给为主，蒸发、向地表水泄流以及人工开采是地下水的主要排泄方式。区内地下水水位变化受气象、水文、地质、开采及补给等因素制约，而且各因素之间的关系很难确定，难以用简单的线性函数进行描述，故地下水埋深具有随机性[24]。马尔科夫模型把系统看作一个整体，对所研究的系统进行状态划分，研究系统从一个状态到下一个状态的转移规律，符合地下水埋深随机变化的特点。同时研究区地下水水位连续监测数据达30年以上，基本具备了进行马尔科夫方法应用研究的基础。鉴于此，笔者采用加权马尔科夫链建立淮北平原西部地下水埋深动态预测模型，预测研究区地下水埋深所处的区间值，将模糊集理论的隶属度和级别特征值引入预测中，实现了对地下水埋深具体值的预测，拓展马尔科夫链模型在地下水动态预测中的应用，同时为该地区地下水资源管理与决策提供一种新的方法。

2加权马尔科夫链预测模型的应用

2.1研究区概况

研究区包括亳州、阜阳、界首、涡阳、太和、利辛、临泉、阜南、凤台9个县市，面积1.81万km2。地处皖豫交界，交通便利，铁路有京九线、淮阜线、濉阜线、阜漯线等，公路交通有界阜蚌高速公路、105国道和以亳州、阜阳为中心的交通干线。

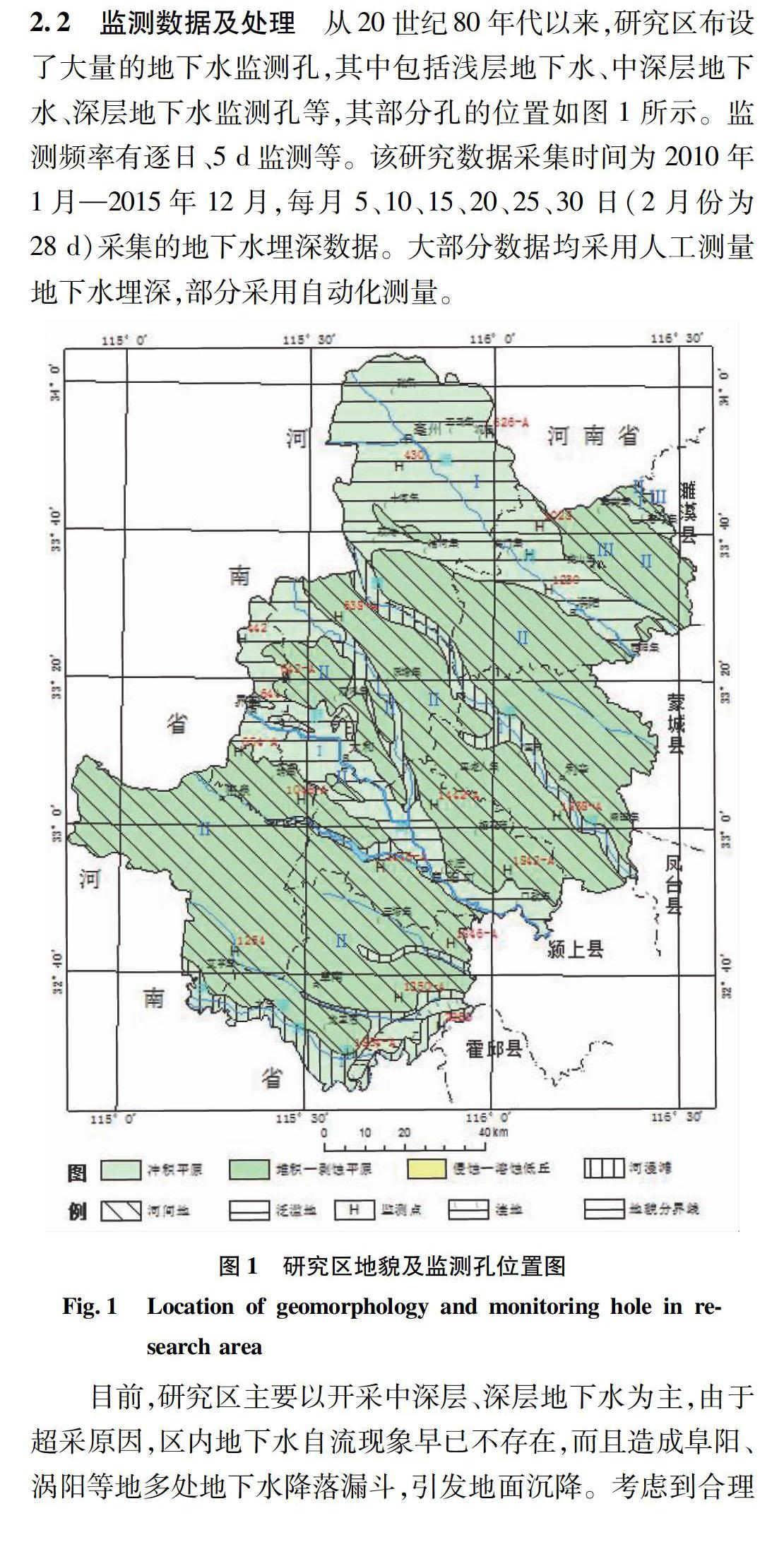
研究区属典型黄淮堆积型地貌，由泛滥微高地、泛滥坡平地、决口扇形地、河间洼地、河间平地、河漫滩等微地貌组成。除在研究区东北部的涡阳龙山局部有零星的溶蚀低丘分布;东部及南部为冲积-剥蚀平原，地形平坦，总体由西北向东南缓倾，地面标高20～42m。

研究区属暖温带半湿润季风气候区，具有明显的过渡性气候特征，四季分明;多年年平均气温14.7℃，多年平均降雨量808.6mm，多年平均蒸发量1604.2mm。

研究区河流属淮河水系，区内地表水系发育，呈平行、等距展布。流向大体均为120°，由北西向南东斜贯本区注入淮河。主要有淮河及其支流颍河、泉河和西淝河，均自西北流向东南;其次有黑茨河和涡河等，其中颍河、泉河为2条较大河流。

根据研究区现有地下水埋深监测资料，结合该研究的确定的分级标准可以推断出，研究区地下水埋深状态为3的机会最多，平均每隔1.76年出现1次，出现的概率为0.5658，即研究区中深层地下水埋深处在[5.080，5.960）的机会最大，对于状态5每隔3.65年出现1次的概率为0.2742，即地下水埋深在[6.448，+∞）出现的概率也偏高，即在不合理开发利用地下水情况下，研究区地下水埋深将呈增大趋势。

同理，按照上述的原理、方法以及步骤可得到研究区浅层地下水的平稳分布和各状态重现期如表7。

可见研究区浅层地下水埋深状态为3的机会最多，平均每隔3.43年出现1次，出现的概率为0.2917，即研究区地下水埋深处在[2.925，3.635）的机会最大;地下水埋深状态2，地下水埋深[2.570，2.925）出现的机会最少，平均每隔8.56年出现1次，出现的概率为0.1168;对于状态5每隔4.90年出现1次，即地下水埋深[3.990，+∞）出现的概率也偏高，浅层地下水埋深也在逐年增加。不难发现，研究区地下水埋深均呈现增大趋势。

3结论

在水资源评价中，地下水埋深动态变化、预测是一项重要的内容，目前存在较多的预测评价模型。该研究基于权马尔科夫链模型对淮北平原西部地下水埋深进行了预测研究，获得了一些认识。

（1）地下水位埋深是地下水补、径、排等条件信息的综合体现，利用马尔科夫链模型，考虑历史信息，对地下水埋深进行预测，在一定的条件下可以获得较高精度的预测。

（2）该研究将模糊集理论中的隶属度和级别特征值引入到预测模型中，实现了对地下水埋深具体值的预测，拓展了模型的预测能力。

（3）应用遍历定理，计算序列的极限分布表明，研究区中深层地下水多处于[5.080m，5.960m），处于[6.448m，+∞）出现的概率也偏高;浅层地下水埋深多处于[2.925m，3.635m），处于[3.990m，+∞）也呈现增大趋势，在地下水资源不合理的开发利用下，区地下水埋深呈增大趋势。

（4）水资源管理部门应对该地区地下水资源提出科学的管理措施以应对地下水埋深增大的变化趋势，防止地下水超采引发地下水漏斗、地面沉降等环境地质问题。

参考文献

[1]杨金忠，蔡树英.地下水动态预报的多层递阶组合模型[J].水科学进展，1995，6（2）：101-106.

[2]李榮峰，沈冰，张金凯.考虑周期性变化的地下水埋深预测自记忆模型[J].农业工程学报，2005，21（7）：34-37.

[3]李文超，胡天然，魏永霞.BP-ANN模型在地下水动态预测中的应用研究[J].东北农业大学学报，2009，40（9）：44-47.

[4]张忠永，王明涛，贾惠艳.人工神经网络在地下水动态预测中的应用[J].辽宁工程技术大学学报，2002，21（4）：504-506.

[5]付强，门宝辉，王志良，等.非平稳时序模型在三江平原井灌水稻区地下水动态变化中的应用[J].系统工程理论与实践，2003（1）：132-138.

[6]高黎明，李林.优化GM（1，1）模型在预测地下水埋深中的应用[J].塔里木大学学报，2005，17（1）：11-13.

[7]杨忠平，卢文喜，李平.时间序列模型在吉林西部地下水动态变化预测中的应用[J].水利学报，2005，36（12）：1475-1479.

[8]王新民，崔巍.变权组合预测模型在地下水水位预测中的应用[J].吉林大学学报（地球科学版），2009，39（6）：1101-1105.

[9]喻黎明，严为光，龚道枝，等.基于ELM模型的浅层地下水位埋深时空分布预测[J].农业机械学报，2017，48（2）：215-223.

[10]孙才志，林学钰.降水预测的模糊权马尔可夫模型及应用[J].系统工程学报，2003，18（4）：294-299.

[11]夏乐天，朱元甡，沈永梅.加权马尔可夫链在降水状况预测中的应用[J].水利水电科技进展，2006，26（6）：20-23.

[12]王亚雄，黄淑娴，刘祖发，等.变化环境下北江下游年径流量的加权马尔可夫链预测[J].生态环境学报，2011，20（4）：754-760.

[13]杜川，梁秀娟，王中凯，等.改进灰色-马尔科夫模型在年降水量预测中的应用研究[J].节水灌溉，2014（6）：32-36.

[14]龙珂良，陈星，崔广柏，等.基于马尔科夫模型下的水质评价[J].水资源保护，2016，32（2）：133-138.

[15]范丽丽，邱利，田威，等.基于马尔科夫模型的太湖水质综合评价[J].水资源保护，2015，31（2）：50-54.

[16]周秋文，苏维词，陈书卿.基于景观指数和马尔科夫模型的铜梁县土地利用分析[J].长江流域资源与环境，2010，19（7）：770-775.

[17]刘少佳，任志远，杨文艳，等.基于马尔科夫模型土壤侵蚀动态变化研究：以西安都市圈为例[J].水土保持研究，2015，22（5）：14-19.

[18]杨琦，杨云峰，冯忠祥，等.基于灰色理论和马尔科夫模型的城市公交客运量预测方法[J].中国公路学报，2013，26（6）：169-175.

[19]芮海田，吴群琪，袁华智，等.基于指数平滑法和马尔科夫模型的公路客运量预测方法[J].交通运输工程学报，2013，13（4）：87-93.

[20]梁桂兰，徐卫亚.模糊马尔科夫链状模型在斜坡稳定性预测中的应用[J].中国地质灾害与防治学报，2006，17（4）：64-67.

[21]李杨，唐仲华，方琼.含水层非均质结构的马尔可夫链地质统计方法及应用[J].地质科技情报，2006，25（5）：92-96.

[22]田玉昆，周辉，袁三一.基于马尔科夫随机场的岩性识别方法[J].地球物理学报，2013，56（4）：1360-1368.

[23]宋印胜.马尔可夫链模型在地下水水位预测中的应用[J].山东地质，1998，14（1）：34-40.

[24]李彬，史海滨，李祯，等.基于权马尔科夫链模型的河套灌区上中下游地下水埋深预测研究[J].干旱地区农业研究，2014，32（5）：206-212.

[25]韩璞璞，张生，李畅游，等.基于权马尔可夫链模型的庐江县降水量预测[J].水文，2012，32（3）：38-42.