基于层次分析法的水产活体运输方法选择研究

赵晨阳 陈增

摘要：本文在调查访问的基础上运用层次分析法对水产活体在运愉中的成活率问题进行了研究，通过比较分析五种水产运输方法，其优先顺序为：塑料袋充氧运愉>麻醉运输>充氧剂运输>机组运输>超低温运输。

关键字：水产运输;成活率;层次分析法;优先顺序

1 前言

水产活体运输中的成活率问题一直是该行业关注的重点，目前针对成活率问题的研究多是通过实验的方法分析耗氧量、成活率的关系[1-4]，鲜有研究考虑交易成本、操作步骤、以及成活率对水产活体运输的影响，由于运输方式的多样，许多鱼商面临着选择哪一种运输方式更经济合理的问题，本文通过层次分析法对六种不同运输方式进行分析比较，给出其优先顺序，对水产活体运输方法的时机选择有指导意义。

2 水产活体不同运输方法的比较分析

2.1 条件假设

考虑：现有一个水产商家接到一份订单要买1000条活的大黄鱼，水产商家在上海的A地，要把这1000条活鱼运往北京的B地，假定从A地到B地就有麻醉运输，充氧运输，超低温运输，机组运输，氧气运输剂运输，商家如果只考虑三个要素，交易的总成本C，操作步骤O，成活率L.商家应该选择哪一种运输方式最满意？通过调查访问一些鱼商，并让这些鱼商从三个维度给出了交易成本、操作步骤、成活率在水产活体运输中的重要感知程度。通过层次分析法进行分析。

2.2 层次分析法

层次分析法是美国匹兹堡大学教授Saaty于20世纪70年代初期，在研究“为國家各工业部分分配电力”的课题时，合理地将决策目标分解出多个准则，进而再分解为多个指标的层次[5]。

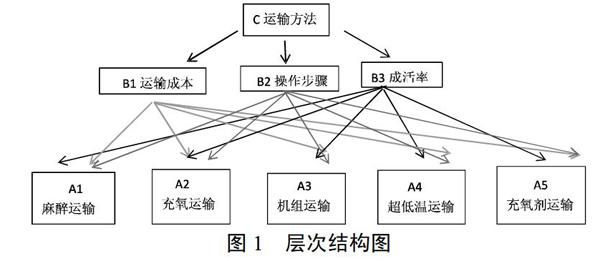
2.2.1 建立层次结构模型

其中第一层为目标决策层，第二层为准则层，第三层为方案层，如下图所示：

2.2.2 确定评价基准或标度

1，3，5，7，9分别表示一个因素比另一个同样重要、稍微重要、较强重要、强烈重要、绝对重要，2，4，6，8为中间值，表示需要在两个标准之间取折中值。

2.2.3 从最上层开始，依次以最上层要素为依据，对下一层要素两两比较，建立判断矩阵。

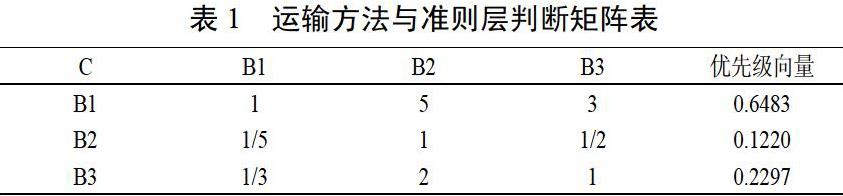
a.先以第一层元素（运输方法）为依据对第二层（准则层）要素建立判断矩阵如表：

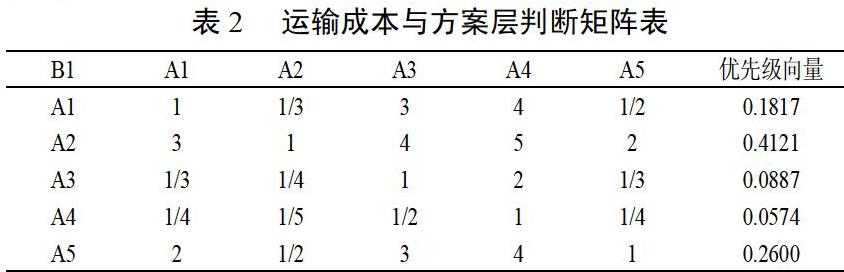
b.在以第二层要素（准则层）为依据，对第三层（方案层）要素建立判断矩阵，由于此时有三个准则，故有三个判断矩阵。

2.2.4 根据判断矩阵，计算各要素的优先级向量

首先计算表1判断矩阵各要素的优先级向量，由于此时判断矩阵为3*3矩阵，根据方根法则首先计算矩阵各行元素乘积的3次方根。B1：（1*5*3）"3=2.4662，B2=（1/5*1*1/2）^1/3=0.4641，B3=（113*2*1）^1/3=0.8736，其次将上述计算结果正交化，即先将上述个数加和，再除以每个数，这样就得到了表2中各要素B1，B2，B3的优先级向量。

2.4662+0.4641+0.8376=3.8039，B1：2.4662/

3.8039=0.6483，

B2：0.4641/3.8039=0.1220，

B3：0.8376/3.8039=0.2297，同理得出其它矩阵的优先级向量。

2.2.5 一致性检验：

由公式：CR0CI/Rl，其中RI可以根据查表得出，CI可由公式CI=入max/（n-1）计算出来。以表1为例：

判断矩阵，W：优先级向量。

最大特征根为：

入max=（1.9474/0.6483+0.3666/0.1220+0.6898/0.2297）^1/3=3.0039

则：CI=入max/（n-1）=（3.0093-3）/（3-1），所以CR=CI/RI=0.0020/0.58=0.0034<0.1，同理计算表2，表3，表4，其CR值分别为：0，0306，0.0190， 0.0160。由CR值可知均通过一致性检验。

根据总体优先级向量可知，麻醉运输的总体优先级为0.2396，充氧运输的总体优先级为0.3020，机组运输的总体优先级为0.1753，超低温运输的总体优先级为0.1359，充氧剂运输的优先级为0.2160，可以认为5个方案的排序应为：A2>A1>A5>A3>A4，即塑料袋充氧运输>麻醉运输>充氧剂运输>机组运输>超低温运输。

3 结论

通过对五种运输方法用层次分析法进行分析，考虑操作步骤、成活率、成本三个因素，给出了五种运输方法的优先顺序，分别为：即塑料袋充氧运输>麻醉运输>充氧剂运输>机组运输>超低温运输。

参考文献

[1]张三龙，蔡天治.提高夏季活鱼运输成活率的试验[J].水产养殖，1990（02）：17-19.

[2]韩杰，孟军.提高活鱼运输成活率的技术要点[J].渔业现代化，2006（01）：49.

[3]黄啸，陆茵.水产活体流通运输的研究现状[J].浙江农业科学，2010（02）：431-434.

[4]张耀明，康焕春.利用双氧水（H_2O_2）作增氧剂运输鱼苗的试验[J].水产科学，1983（01）：29-31

[5]崔运鹤，钱平，苏晓鹭.基于层次分析法的动态指标体系管理系统及其应用[J].地球信息科学，2007（01）：93-98+103.