某轿车通风盘式制动器有限元模态分析
李 飞郑忠才高 岩单 萍李 达
(1-山东建筑大学机电工程学院 山东 济南 250102 2-山东电子职业技术学院)
引言
在制动系统中,制动器的性能和质量是汽车安全行驶的重要保障。制动器性能的好坏影响到汽车整体的制动性能,从而影响到汽车的行驶安全性。因此,在研究和设计车辆的过程中,改善车辆的制动性能,提高制动器的设计和制造水平具有非常重要的现实意义。在国内,盘式制动器有限元仿真分析主要集中在一些高校及企业,针对制动盘及摩擦片的结构或制动盘温度场等方面进行分析,噪声和振动也成为制动器有限元分析的一大热点。同济大学的张立军等人通过有限元分析法,对制动盘进行36阶自由模态及预应力模态分析,通过分析不同阶模态振型图,揭示约束条件对制动盘结构模态特性的影响机制[1]。湖南大学的匡博对噪声进行分析,通过复模态分析,分析固有频率[2]。
1 盘式制动器有限元模型建立及研究方法
1.1 盘式制动器有限元模型建立与简化
在对盘式制动器做仿真分析时,对制动盘进行简化,将制动钳、防护罩、液压缸等部件忽略,仅对制动盘和制动摩擦片进行分析。本文针对某款制动器进行建模分析,制动盘为浮钳盘式。图1为制动器实物图,对其进行简化并建立三维模型。

图1 制动器实物图
制动盘的最大直径为300 mm,中心凸台直径为155 mm,中间圆的直径为65 mm,定位孔的直径为12 mm,总厚度为26 mm,其中散热孔宽为10 mm,形状为矩形。忽略制动盘倒角、圆角等不影响制动盘制动性能的次要因素,进行建模。模型的三维视图如图2所示。

图2 制动盘模型
本文所用制动盘的材料为HT250,摩擦片为树脂基复合材料,其物理性能参数如表1所示,2者接触摩擦系数为0.2[3]。

表1 制动器材料属性
1.2 有限元法分析的基本步骤
物体在力作用下的平衡规律是静力学分析的主要研究方向,静力学分析虽不及动力学分析应用广泛,但在实际应用中也是十分重要的。在固定载荷作用下,静力学探讨的是物体变形后应力、应变的分布情况。
1.2.1 物理模型离散化(划分网格)。
将模型离散为由各个单元组成的计算模型,称为单元离散。一般情况下,单元划分越密,则应力描述越精确,越接近实际情况,但所需的计算时间也越长,因此,应根据实际情况合理划分[4]。另外,通过有限元分析得到的结果是近似的,最终获得的结果只是无限接近实际情况。
1.2.2 定义单元特性
1)位移模式的选取。在有限元分析中,位移法应用最广。使用位移法时,未知量可以被节点位移替换,用函数表示,此时需要找出关系式来表示位移和节点力的关系,这一步很重要。
2)计算等效节点力。对于实际连续体,力的传递是通过单元体之间的分界面。对于离散体,可假定力是通过节点来进行传递的,因此,节点上的力能否等效转移是很重要的。
3)组装单元。在结构不变的情况下,每个单元通过组合,形成有限元分析方程。
4)求解未知节点位移。分析计算后,通过解析有限元方程,可得到位移。约束和载荷都属于边界条件,分析模型质量的精确与否很大程度上和施加在有限元模型上的边界条件有关,Workbench15.0主要涉及惯性载荷、结构载荷、热载荷等。本文主要考虑转动约束、位移约束、接触面摩擦约束等。
2 模态分析
2.1 模态分析方法
模态分析是分析结构自然频率和模态形态的方法[5],在分析中假设:
1)结构刚度矩阵和质量矩阵不发生变化;
2)除非指定使用阻尼特征求解方法,否则不考虑阻尼效应;
3)结构中没有随时间变化的载荷。
在无阻尼系统中,结构振动方程为:

对于线性系统而言,自由振动满足下列方程:

式中:{φi}为第i阶模态形状的特征向量;ωi为第i阶自然振动频率;t为节点加速度向量。
由公式(1)和公式(2)可以得出:

从公式(3)中可得结构的振动特征方程为:

通过公式(4)可以求出第i阶自然振动频率ωi,进而求出第i阶模态形态的特征向量{φi}。将{φi}对质量矩阵[M]进行归一化处理,可以得到:
如果对{φi}进行归一化处理,那么{φi}中最大向量坐标将归一化为1.0[6]。

2.2 自由模态分析
本文中,制动盘的自由模态状态为制动盘通过轮毂固定,有一个固定约束,制动摩擦片与制动盘没有接触,因在导入模型时已经添加约束,故此处连接设置为无摩擦连接(frictionless)。
2.2.1 盘式有限元模型的建立
盘式有限元模型的建立主要基于以下几个步骤进行:导入制动器的简化模型,定义制动盘和摩擦片的材料属性,按不同的尺寸进行网格的划分。具体步骤为:
1)导入简化模型;
2)定义有限元模型材料;
3)添加模型的材料属性;
4)创建接触关系;
5)划分网格。
在本文的自由模态分析中,采用协调分片四面体划分方式对制动盘三维模型进行网格划分,如图3所示。为了便于收敛,在接触面周围采用映射面网格划分,划分后包含节点总计78594个,单元44687个,网格相关度设置为60,模型划分后结构单元如表2所示。
2.2.2 仿真结果分析
查看结果应注意2种状况:
1)结果给出频率列表,可以选择某一频率查看振型。

图3 网格划分图
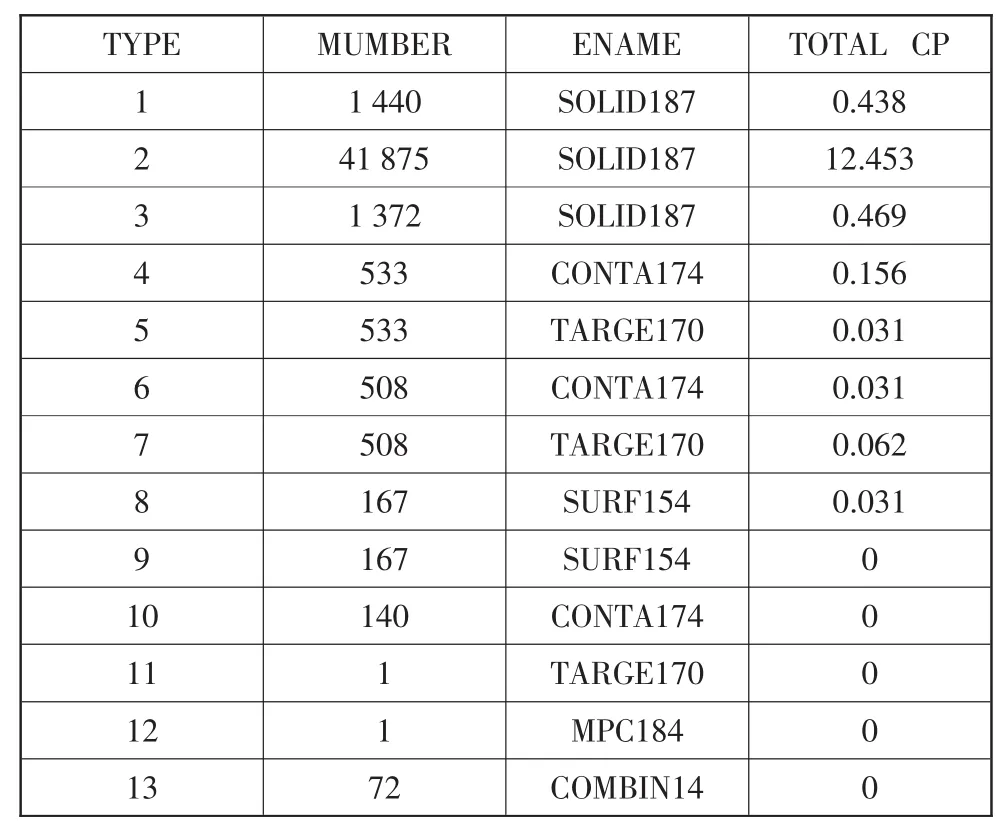
表2 结构单元名称及类别
2)振型有利于理解结构的振动,但不代表真实的位移。
图4~图9为自由模态振型图。表3为自由模态各阶频率。从图4~图9以及表3可知,第3阶为振型变化最大状态。第1阶、第2阶振型频率分别为649.23 Hz、670.66 Hz,位移由 27.856 mm 变化为25.079 mm。从第1阶到第2阶变化过程,共振区域从原来Y轴向X轴方向变化,主振型集中在制动盘的边缘略向Z轴轻微变动。第3阶振型以X轴为对称轴,两端沿Z轴正向上下摆动为主振型;第4阶振型以中心对称上下扭转弯曲为主振型;第5阶、第6阶振型基本稳定。

图4 第1阶自由模态分析

图5 第2阶自由模态分析

图6 第3阶自由模态分析

图7 第4阶自由模态分析

图8 第5阶自由模态分析

图9 第6阶自由模态分析

表3 自由模态各阶频率
由上述自由模态分析可知,制动盘振型最大部位变形量主要分布在制动盘的外边缘。产生这种情况的主要原因是制动盘固定位置为中心定位孔处,存在约束,使得振动过程中变化较小甚至基本无变化。
2.3 预应力模态分析
预应力模态分析用于计算有预应力结构的固有频率和振型[7],本文对一定转速下不同载荷预应力进行模态分析。预应力模态分析首先涉及的是静力学分析,然后将分析结果导入模态分析中进行求解。
制动盘预应力模态分析中的静力学分析流程是先添加约束后进行结果分析。首先点击Connections,进行接触类型的选择。通过建立制动盘与摩擦片的关系,一方面可以防止部件的相互渗透,另一方面提供了部件之间载荷传递的方法,方便后面载荷的有效施加与作用[8];其次添加各类约束;最后进行仿真结果分析。
经分析发现,不同预应力作用下,振型变化基本相同。本文选取3 MPa为例进行6阶预应力模态分析。
图10~图15为预应力模态振型图。从图10~图15可知,第5阶为振型变化最大状态。第1阶振动频率为402.29 Hz,振型基本没有变化;第2阶、第 3阶振型频率分别为 738.13 Hz、740.57 Hz,最大可能位移由26.245 mm变化为26.667 mm;从第2阶到第3阶变化过程,振型从原来Z轴负方向向Z轴正方向变化,主振型集中在制动盘的边缘略向Y轴轻微变动;第4阶振型以X轴为对称轴,两端沿Z轴正向上下摆动为主振型;第5阶振型以中心对称上下扭转弯曲为主振型;第6阶振型整个曲面发生较小振动。

图10 第1阶预应力模态分析

图11 第2阶预应力模态分析

图12 第3阶预应力模态分析

图13 第4阶预应力模态分析

图14 第5阶预应力模态分析
由上述预应力模态分析可知,制动盘振型最大部位变形量主要分布在制动盘的外边缘,产生这种情况的主要原因是:
1)因为制动盘固定位置为中心定位孔处,存在约束,使得振动过程中第1阶变化较小甚至基本无变化;
2)制动盘与摩擦片接触处存在约束,使得振动过程中第2阶~第3阶变化较小。
通过振型图的分析,在静力学分析中得到制动盘与摩擦片接触处应力最大,约为16.931 MPa,有应力集中的情况。因此,为了避免因发生共振导致制动盘运动不稳造成结构损坏,设置外界激励频率不能接近或等于第5阶模态固有频率。
2.4 不同预应力状态下模态分析
采用上述研究方法进行不同载荷量设置,然后进行仿真分析,结果如表4所示。根据表4中的数据所绘制的不同预应力状态下1~6阶预应力模态和自由模态的频率变化曲线如图16所示。
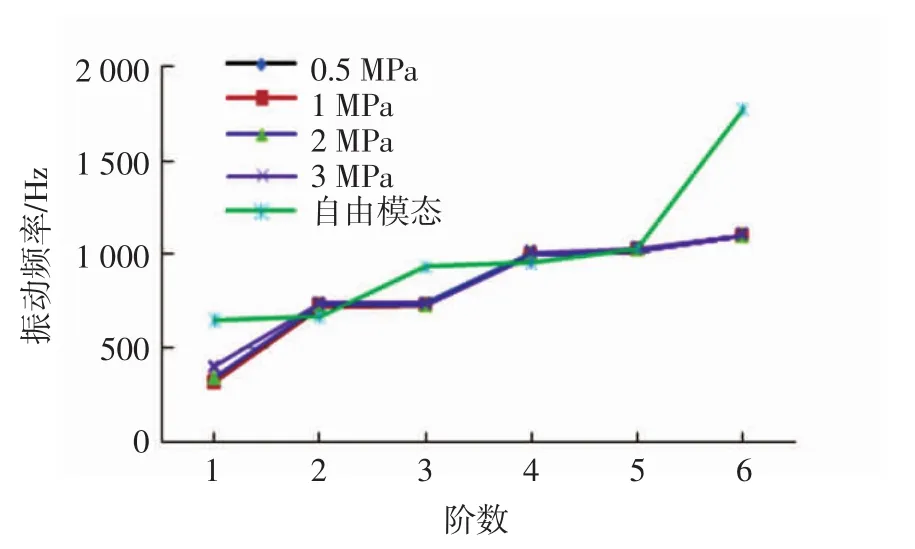
图16 不同预应力状态下1~6阶预应力模态和自由模态的频率变化对比折线图
从图16可知,在不同预应力状态下(0~3 MPa),制动盘的振动频率与施加载荷的大小关系不大。即在一定运转状态下,施加载荷的大小对制动盘的振动影响较小。相比于自由模态的振型,在预应力状态下,即使有载荷施加,主振型形状也基本相同,不同在于载荷的施加使得共振推迟,并且主振型所沿坐标轴方向发生了改变。

表4 不同预应力下模态分析数值统计表
3 结论
通过上述研究表明:
1)自由模态状态下,主振型在第3阶以X轴为对称轴,两侧向Z轴正方向摆动。
2)通过仿真发现,相比于自由模态的振型,在预应力状态下,不管有无载荷施加,其整体主振型形状基本相同,不同在于载荷的施加使得共振推迟,并且整体主振型形状相近,但主振型所沿坐标轴摆动方向发生了改变。
3)通过仿真发现,在不同载荷下,共振点位置及区域在变化。故在制动盘运转过程中,要避开共振区域,设置外界激励频率不能接近或等于模态固有频率。

