多蛋形交接耐压壳屈曲特性试验与数值研究
左新龙,唐文献,3,张 建,,王纬波,王月阳,吴文伟
(1.江苏科技大学,江苏 镇江212003;2.中国船舶科学研究中心,江苏 无锡214082;3.江苏科技大学 江苏省船海机械装备先进制造重点实验室,江苏 镇江212003)
0 引 言
2016 年2 月,国家公布了深海海底区域资源勘探开发法,从法律层面支持包括深海潜水器在内的深海科学技术装备研发。近两年,科技部把“深海关键技术与装备”作为重点专项,列入国家重点研发计划,支持原创性深海潜水器研发及深海前沿关键技术攻关。
耐压壳体作为潜水器的内部壳,保证潜水器内部恒定的大气压力。潜水器的耐压壳体组成一个水密空间,是潜水器浮力的主要提供者,其重量占潜水器总重量的1/4~1/2[1-2],耐压壳体结构形式的选择直接影响到潜水器的有效载荷[3]。现役壳体结构仍存在应力集中及空间占用率低等缺点[4-5],对于单球形耐压装备,在实际受载过程中,由于对缺陷非常敏感,发生失稳时的压力仅为理论值的1/4~1/3[6],安全性较差;单球形耐压装备只能通过依靠增大球半径来增大内部空间,半径的增大会导致水阻力增大,降低潜水器的机动性;球形耐压装备曲率较小且处处相等,导致内部设备布置困难,空间利用率较低,人员舒适性变差,进而降低潜水器的人机环特性。多球形耐压装备在一定程度上扩大了舱室空间,提高了人员舒适性,但仍然无法克服缺陷敏感度高、空间利用率低等缺点。因此,对于新型壳体结构的研究依然很迫切。
新型耐压壳体应避免球形、椭球形等壳体缺点,且具有轻质、高强度等特点,以满足潜水器长时间作业的需求。因此,能最优协调缺陷敏感度、空间利用率等优点的异形壳的探索性研究显得尤为重要。Magnucki[7]认为交接的桶形耐压壳可以替代传统的圆柱形和球形耐压壳。Jasion[8-10]提出了分别由定常经线、卡西欧卵形线及回转球形曲线等旋转壳体交接而成的耐压壳,并进行了详细的试验及理论研究。Blachut[11-13]也对由定常经线旋转壳体交接而成的耐压壳进行了试验研究,得到了加强肋对壳体失稳破坏的规律。蛋壳是一种母线为正高斯曲线的典型回转壳体,具有良好的重量强度比、跨距厚度比、流线型、美学特性、合理的材料分布等优点。蛋壳满足圆顶原理,无需肋骨支撑,利用最少材料即可获得足够的强度和稳定性。在均布外压作用下,蛋壳可通过面内压力抵抗外载荷,表现出较强的抗压特性,是一种优异的耐压壳仿生设计原型[14-16]。鉴于上述优点,本课题组对清除内容物的舟山鹅蛋进行了静水压力试验,发现其平均抗压能力为3 MPa,相当约1.7 t 的握紧力。
为此,本课题组首次尝试将蛋形结构引入到深海耐压装备结构创新设计中,研究发现蛋形耐压壳对几何缺陷的敏感程度较低,屈曲载荷衰减系数仅为等效球壳的60%-80%,因而对加工精度要求可适当放宽;蛋形耐压壳是一种具有良好流线型的扁长卵形壳,且较小的旋转半径可缩小水流冲击面,水动力学特性优于球壳,同时较小的旋转半径也可降低制造难度和加工误差;蛋形耐压壳经向曲率半径远比等效球壳高,便于内部设备布置,增加空间利用率,其独特的蛋形空间可提高乘员舒适性,进而提高潜水器的人机环特性。此外,蛋形耐压壳便于在端部开设人孔和观察窗,在低频阶段具有良好声学特性[17-19]。预研结果表明,蛋形耐压壳可最优协调几何缺陷敏感性低、空间利用率高、水动力学特性好等优点,在深海潜水器上具有广阔应用前景[20-21]。
对于单蛋形耐压壳(简称为单蛋壳)结构的潜水器,其单舱室空间较小,无法满足大空间深海潜水器开发的要求。张建[20]提出了多蛋形交接耐压壳(简称为多蛋壳)结构,在去除蛋形壳曲率较大的两端下,进一步提高了空间占用率;研究了交接环肋尺寸的影响规律,为避免出现交接环肋刚度过大或不足,使壳体开孔处的变形量与完整壳体一致,保障交接后的蛋形壳的力学性能及稳定性不受影响,确立了蛋形壳开孔前后变形一致的设计理念(简称为变形协调)[20]。然而,变形协调理念设计下的加强环肋尺寸参数合理性,及真实多蛋壳破坏形式需要通过试验进一步验证。
因此,本文开展多蛋形交接耐压壳屈曲特性试验研究工作。首先,基于变形协调理念,优选多蛋壳结构参数,制作树脂多蛋壳比例模型作为试验对象;接着,通过逆向工程获取真实多蛋壳三维模型,对比例模型的圆度及制作误差进行了检测;最后,进行静水压力试验,验证真实多蛋壳破坏形式,检验变形协调理念设计的环肋参数合理性,比较了考虑真实形状和厚度的非线性有限元分析结果。
1 试验材料
前期研究发现蛋形壳一端或双端开孔,及交接蛋形壳的个数,对其结构性能并无影响[20]。考虑静水压力模拟设备内腔容积,以双蛋形交接耐压壳(简称为双蛋壳)为例,进行试验研究。
双蛋壳由两个相同的蛋形壳对称交接而成,参考一般深潜器壳体的结构尺寸,采用无肋骨壳体形式,几何模型如图1 所示。选用与鹅蛋壳轮廓吻合程度较好的Kitching 蛋形曲线作为蛋形壳外轮廓[20],且取B/L=0.69、L/e=45。此外,前期研究发现,双蛋壳以尖、钝端两种对称相交的结构性能基本一致。为进一步提高空间占用率,去除曲率较大尖端,采用尖端对称交接的结构形式,其中主要几何参数包括:双蛋壳长度Lm、宽度Bm、蛋形壳厚度t、加强环肋长度Lr、双蛋壳交接开孔直径Rr(即环肋外直径)和环肋厚度tr(图1)。
金属材质的异形壳多为冲压、焊接工艺,原有的蛋形轮廓很难保证。 采用工艺性较好的三维打印技术,选用8000 ABS 树脂,250-300 nm 波长照射下完成固化。许用应力[σ]=20 MPa,弹性模量E=2 600 MPa,泊松比μ=0.34。为避免出现交接环肋刚度过大或不足,使壳体开孔处的变形量与完整壳体一致,保障交接后的蛋形壳的力学性能及稳定性不受影响,作者前期研究工作中确立了蛋形壳开孔前后变形一致的设计理念[21]。基于变形协调设计理念,尖端对称交接的双蛋壳几何参数如表1 所示。
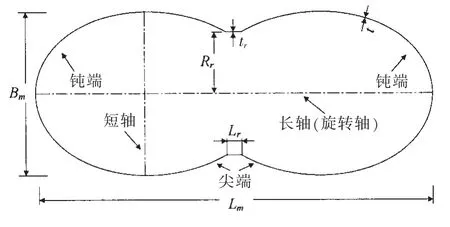
图1 双蛋壳几何模型Fig.1 Geometry of the double-segment egg-shaped shell

表1 双蛋壳几何参数Tab.1 Geometric parameters of the double-segment egg-shaped shell

表2 双蛋壳比例模型Tab.2 Scale models of double-segment egg-shaped shells
为检验变形协调理念设计的环肋参数合理性,制作无环肋加强及加强环肋厚度为tr=2 mm 的比例模型作对比,相同参数的比例模型均制作两个,以作参考及验证试验可重复性。联系深圳某未来工厂厂家,采用3D 打印技术加工6 件8000 ABS 树脂材料的尖端交接双蛋壳比例模型,见表2。为方便取出支撑物,均在双蛋壳一端开小孔,三维扫描及静水压力试验时,用胶水将其连接,各比例模型的环肋参数如表3 所示。
2 试验方法
2.1 圆度与制作误差检测
试验仪器选用Open Technologies 公司的手动三脚架3D 扫描仪 (单笔扫描范围:150×115×150 mm;扫描仪像素:200 M;精度:0.02 mm),针对已制作的6 个双蛋壳比例模型,规范操作,获得三维模型,如图2 所示。
针对6 个双蛋壳比例模型,随机截取沿双蛋壳旋转轴的三个截面。其截面的外形线(或称经络线),所在面夹角互为120°,由此可避免选取的经络线过于集中,2-1#双蛋壳所在三个截面的蛋形经络线,如图3(a)-(c)所示。每个双蛋壳的三条经络线及与Kitching 蛋形曲线的皮尔逊相关系数,如表4 所示。
分析结果发现,每个双蛋壳的三条经络线的相互皮尔逊相关系数均大于0.999,且与Kitching 蛋形曲线的相互皮尔逊相关系数也大于0.999,证明制作的双蛋壳是高度对称的旋转壳,且与Kitching 蛋形曲线高度一致。

表3 双蛋壳比例模型几何参数Tab.3 Geometric parameters of six doublesegment egg-shaped shells

图2 三维扫描试验Fig.2 3-D scanning test

图3 2-1#号双蛋壳上的三条蛋形经络线Fig.3 Three contours of 2-1#goose egg

表4 双蛋壳轮廓线的相互皮尔逊相关系数(PPMCC)Tab.4 PPMCC of six double-segment egg-shaped shells’contours
GOM Inspect 三维检测软件,常作为三维扫描后处理,用于检测对象与理想轮廓的误差,分析结果如图4 所示,图标为真实双蛋壳与理想轮廓基于曲率半径的误差及误差频率。相同轮廓的真实双蛋壳误差及各误差段出现的频率近乎一致,说明加工过程中并没有出现较大波动,相同参数的两个双蛋壳在后续试验中具备相互参考性。0-1#和0-2#双蛋壳与理想轮廓最大曲率半径误差为0.24 mm,误差在0.04-0.16 mm 之间,占总误差段的98%以上,其中两顶端误差最大。2-1#和2-2#最大曲率半径误差为0.42 mm,误差多在0.06-0.36 mm 之间。7-1#和7-2#最大误差0.58 mm,误差大多在0.20 mm 左右。考虑三维扫描设备精度0.02 mm,后处理曲面造型及软件系统误差,可以确定该6 个双蛋壳比例模型近乎完美壳体,可以用于静水压力试验研究,其结果具有较高参考价值。

图4 误差检测Fig.4 Error inspection
2.2 静水压力试验
静水压力模拟试验设备为本课题组自主研发,使用空气增压泵为动力源,以气液增压泵为压力源,输出水压与驱动气源成比例,可实现对水压的无级调节。压力舱内的水压通过压力传感器(量程:0~10 MPa,精度:±0.1%)实时采集,采样频率为50 Hz。
将树脂双蛋壳置于本实验室开发的高压舱水压模拟设备舱体内,外接水泵,先将舱体内腔注入清水,且不宜过满,留足上端封盖可顺利与舱体啮合的空间。由于试验对象为树脂双蛋壳,在高压舱中的浮力较大,若直接进行压力试验,高压舱盖会对试验对象顶部产生扰动力,影响试验结果。为此,使用材质柔软的网兜包住壳体,并在下端挂上重物,保证悬浮在水中。接通换向阀,上下移动装置动作,将舱体密封,打开高压针阀,并继续通过气液增压泵对舱体内腔注水加压。待有清水从高压针阀流出后,关闭高压针阀。试验对象为树脂双蛋壳,考虑破坏压力较小,增压不宜过快,采用手动阀逐步加压,一旦舱体内出现瞬间压降,停止加压,调节高压针阀对舱体内腔泄压,最后打开上端封盖,取出被测树脂双蛋壳。规范操作0-1#和0-2#双蛋壳比例模型静水压力试验过程,高压舱内腔压力变化如图5 所示。
图5 为0-1#和0-2#双蛋壳比例模型静水压力试验高压舱内压力曲线,横坐标为数据采集时间,纵坐标为高压舱内压力值,选用手动加压方式,压力曲线呈现锯齿式增加趋势。曲线峰值即为样本破坏时的最大外压载荷。0-1#与0-2#相同尺寸参数的样本破坏时最大外压载荷悬殊仅为5.2%,同样,2-1#与2-2#、7-1#与7-2#悬殊分别为11.6%和2.8%。因此,针对6 个双蛋壳比例模型,相同参数的两个样本高压舱内压力曲线,趋势及峰值均呈现较好的一致性,试验结果可重复性较高。

图5 0-1#和0-2#双蛋壳静水压力试验Fig.5 Hydrostatic test of double-segment eggshaped pressure shells(0-1#and 0-2#)
静水压力试验后,通过螺旋测微器测量壳体真实厚度,选取40 个壳体离散点,测量结果如表5 所示。结果表明,相同轮廓的真实双蛋壳厚度均值较相近,离散程度也近乎一致,说明在加工同类型模型时并没有出现较大波动,相同参数的两个双蛋壳在本次试验中具备相互参考性。考虑螺旋测微器精度为0.01 mm,且树脂质地较软,尖端测微器势必使测量值偏小,综合分析可以认定试验对象为完美壳体。

表5 真实双蛋壳壳体厚度Tab.5 Thickness of egg-shaped shells
3 结果与分析
3.1 试验结果分析
表6 为0-1#与0-2#、2-1#与2-2#、7-1#与7-2#双蛋壳比例模型的静水压力试验结果。0-1#和0-2#未经环肋加强的双蛋壳破坏均发生在交接处,2-1#和2-2#双蛋壳环肋刚度不足,其破坏也均发生在交接处;7-1#和7-2#基于变形协调设计的双蛋壳,一个蛋形壳单元中部出现破坏,且远离交接处。因树脂材料塑性一般,延展性较差,具有一定脆性,最终破坏形式存在崩裂,双蛋壳比例模型破坏面积较大,属正常现象。此外,试验样本一端的胶水连接处均未出现破坏,且端部也未见裂痕,表明端部开小孔且胶水连接后,并未对试验结果产生影响。

表6 试验结果Tab.6 Experimental results
此外,本课题组成员针对完整单蛋壳进行了静水压力试验,破坏形式见图6 所示,高压舱内峰值载荷为0.680 MPa,与7-1#和7-2#双蛋壳的破坏载荷相差3%和0.29%(比例模型破坏载荷值见表8)。单蛋壳中部出现崩裂,与7-1#和7-2#双蛋壳的破坏形式一致。说明变形协调设计的环肋参数属于合理范围,双蛋壳继承了完整蛋形壳较好的耐压特性。
3.2 真实壳体非线性屈曲结果分析
针对已制作的6 个双蛋壳缩比模型,因逆向工程获得的模型由许多不规则的曲面片拼接而成,网格划分时采用自由划分局部调整,见图7。各模型几何参数见表1 和表3,材料设定为8000 ABS 树脂,分析结果如图8、表7 和表8 所示。

图6 单蛋壳破坏形式Fig.6 Collapsed form of egg-shaped pressure shell

图7 试验样本数值模型Fig.7 Numerical models of test samples
图8 为7-1#和7-2#真实双蛋壳非线性屈曲平衡路径。纵坐标为载荷比例系数(LPF)(施加初始外载荷为1 MPa,故纵坐标即为承载载荷),横坐标为每一弧长步蛋形壳短轴方向上的最大位移量与蛋形壳厚度的比值。
观察真实双蛋壳非线性屈曲平衡路径,承载载荷首先呈近似线性急剧增大,当到达峰值点后,急剧下降,之后趋于平缓。这种不稳定趋势符合大多数正高斯曲线的旋转壳体非线性屈曲形式。6 个双蛋壳的非线性屈曲平衡路径趋势保持一致,仅峰值不同,7-1#和7-2#临界屈曲载荷最大,2-1#和2-2#次之,无环肋加强的双蛋壳临界屈曲载荷最小,表明经过环肋加强后的双蛋壳临界屈曲载荷明显增大。
表7 分别为0-1#与0-2#、2-1#与2-2#、7-1#与7-2#数值分析结果。0-1#和0-2#未经环肋加强的双蛋壳失稳均发生在交接处,2-1#和2-2#双蛋壳环肋刚度不足,其失稳也均发生在交接处,7-1#和7-2#基于变形协调设计的双蛋壳,一个蛋形壳单元中部出现凹坑,且远离交接处,并最终失效,与试验结果具有较好一致性。

图8 真实双蛋壳非线性屈曲平衡路径Fig.8 Equilibrium paths of the doublesegment egg-shaped shells

表7 数值结果Tab.7 Numerical results
从表8 可见,0-1#与0-2#双蛋壳试验与数值结果相差分别为7.6%和11.9%,二者结构参数一致,仿真结果相差小于0.5%,试验结果相差0.52%。2-1#与2-2#试验与数值结果相差分别为15.1%和2.8%,数值相差小于1.2%,而试验结果相差11.6%,横向及纵向分析均显示2-1#双蛋壳试验载荷值略大,考虑试验传感器及三维扫描精度,属于合理范围内,具备参考性。7-1#与7-2#试验与数值结果相差分别为1.5%和3.6%,数值相差2.5%,而试验结果相差1.3%。试验与数值结果具有高度一致性,且相同结构参数的两个比例模型,数值和试验均呈现较高的一致性,充分说明数值计算和试验过程及结果具有可重复性。

表8 数值与试验载荷值Tab.8 Numerical and experimental maximum external load
图9 为完美双蛋壳的交接环肋厚度对其临界屈曲载荷的影响规律。相同环肋厚度下,真实双蛋壳的试验及数值载荷值与理想双蛋壳近乎相同,也较好说明真实双蛋壳制作工艺成熟,近乎完美。2-1#双蛋壳试验载荷值略大于理想双蛋壳,试验结果存在误差,与上文得出结论一致,但属于合理范围,具备参考价值。综合上述分析,双蛋壳的环肋参数在基于变形协调理念设计后,最终破坏远离环肋交接处,试验与数值验证了变形协调设计理念的合理性。针对6 个双蛋壳比例模型,比较数值分析及试验结果发现,基于弧长法的数值计算与试验结果具有良好一致性,考虑真实形状和厚度的非线性有限元分析可用于分析预测真实壳体的屈曲行为。

图9 加强肋厚度tr 对双蛋壳临界屈曲载荷的影响规律(Lr=15 mm)Fig.9 The influence of thickness on buckling load of the double-segment egg-shaped shell
4 结 论
(1)相同结构参数的试验对象,数值及试验结果一致,可重复性较高,试验材料及方法较为可靠。基于弧长法的数值计算与试验结果具有良好一致性,考虑真实形状和厚度的非线性有限元分析可用于分析预测真实壳体的屈曲特性。
(2)基于变形协调理念设计的多蛋壳,最终破坏远离环肋交接处,试验验证了变形协调设计环肋参数属于合理范围,可避免交接环肋刚度过大或不足引起的壳体破坏。双蛋壳的蛋形壳单元破坏形式及载荷与完整单蛋壳基本相同,试验验证了双蛋壳继承了完整蛋形壳较好的耐压特性。

