轴向载荷下多平面DT 型管节点应力集中系数研究
袁奎霖,杨海天,洪 明
(大连理工大学a.工业装备结构分析国家重点实验室 船舶工程学院;b.工程力学系,辽宁 大连116024)
0 引 言
由于承受风、浪、流等循环载荷作用,疲劳破坏是海洋平台管节点的一种主要失效模式。工程中常用S-N 曲线法对海洋平台管节点的疲劳强度进行评估,即通过计算节点焊缝周围的热点应力幅值来估算该节点的疲劳寿命,其中热点应力幅值的大小由焊缝处的应力集中系数确定。因此,关于管节点应力集中系数的研究对海洋平台结构物的服役安全性评价具有十分重要的意义。常用的海洋工程结构物疲劳设计规范[1]中仅对典型管节点的鞍点和冠点位置提供了应力集中系数计算公式。已有研究[2]发现对于不同的节点几何参数,焊缝周围最大应力点可能位于不同位置,从而影响到疲劳裂纹萌生位置和扩展速度。目前,国内外学者[2-5]关于单一平面T 型、Y 型、K 型、KT 型、X 型等管节点沿焊缝的应力集中系数分布进行了系统的试验和数值研究,并提出了相应的参数公式。然而,上述参数公式对于实际海洋平台结构中更为普遍的多平面管节点难以适用,而关于多平面管节点应力集中系数的研究还鲜有报道。Karamanoes 等[6]提出了多平面DT 型管节点在鞍点和冠点位置处的应力集中系数计算公式。胡维东等[7]对平衡轴向载荷作用下多平面KK 型管节点应力集中系数进行了分析,但未总结出可应用的参数公式。
本文以多平面DT 型管节点为研究对象,建立了352 个具有不同几何形状的有限元模型,对其在两种轴向载荷作用下焊缝周围的应力分布规律进行了分析。基于有限元计算结果,研究了不同几何参数对沿焊缝应力集中系数分布变化规律的影响,并采用非线性回归方法得到一组适用于实际工程应用的多平面DT 型管节点应力集中系数的参数公式。
1 多平面DT 型管节点热点应力分布的有限元分析
1.1 DT 型管节点模型几何参数
本文研究的多平面DT 型管节点几何参数如图1 所示,其中D 为弦管外部直径,d 为撑管外部直径,T 为弦管壁厚,t 为撑管壁厚,L 为弦管长度,l 为撑管长度,φ 为极角,ω 为面外角以及ωinside为两根撑管内部冠点之间的间隙角。文中假定两根撑管具有相同几何尺寸,且两根撑管的中心轴相交于弦管中心轴的中点处,因此间隙角ωinside可由ω 和β 共同确定[8]。

为了研究几何参数对焊缝周围应力分布规律的影响,根据表1 建立了352 个DT 型管节点模型,其中考虑几何参数α、αB、β、γ、τ、φ 和ω 的影响。这352 个模型的几何参数各不相同,而且几何参数的取值范围基本覆盖了实际工程中DT 型节点的几何参数大小。

图1 多平面DT 型管节点几何参数示意图Fig.1 Geometrical parameters of a typical multi-planar tubular DT-joint

表1 多平面DT 型管节点的几何参数Tab.1 Geometrical parameters of multi-planar CHS DT-joints
1.2 有限元模型建立
根据已有研究发现[9],管节点应力分析结果的准确性主要由有限元网格的质量决定。相比于二维壳单元,采用三维体单元能较好地模拟焊缝形状以及沿厚度方向上的应力变化情况。因此,本文将采用ANSYS 中SOLID186 实体单元(20 结点二次六面体单元)建立带焊缝的多平面DT 型管节点模型。材料模型为线弹性体,杨氏模量和泊松比分别为206 GPa 和0.3。
在保证网格质量的前提下尽量减少网格数量以保证计算精度和提高计算效率,采用分区网格划分方法,即把一个管节点模型根据计算结果精度的需要划分成不同的区域,如图2 所示。对于焊缝周围应力梯度较大的区域采用比较精细的网格,而远离焊缝区域则采用相对稀疏的网格。根据预先的网格敏感性分析(见图3),弦管与撑管相贯线附近沿管壁壁厚方向划分3 层单元。此外,焊缝尺寸选取了TAWS,既满足美国焊接协会AWS 标准[10]的最小焊缝尺寸要求又能保证焊缝区域连续光滑地划分网格,也可得到满足工程需要的保守结果(见图4)。

图2 分区法产生多平面DT 型节点的有限元网格Fig.2 FE mesh generation using sub-zone method for multi-planar DT joint

图3 弦管和撑管相贯线附近厚度方向网格敏感性分析Fig.3 Mesh sensitivity study on through-thickness element division nearby the chord-brace intersection

图4 焊缝尺寸对应力集中系数计算结果敏感性分析Fig.4 Effect of the weld size on the SCF
1.3 边界条件与应力集中系数提取
已有研究表明[4],当弦管长度不小于6 倍弦管外部直径时(即无量纲参数α=2L/D≥12),沿管节点焊缝处应力集中系数分布趋于稳定且不受弦管末端边界条件影响,本文中取α=15 且弦管两端刚性固定。如图5 所示某自升式平台桩腿,当受到沿y 方向的外载荷时,DT2 节点类似于平衡轴向载荷工况(见图6(b)),而DT1 和DT3 节点更接近于单轴拉伸载荷工况(见图6(a))。因此,本文中分别对两种轴向载荷工况下焊缝处的应力集中系数分布进行研究。
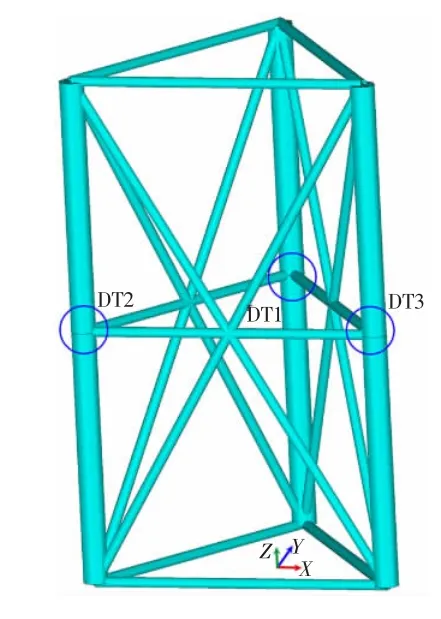
图5 自升式平台桩腿示意图Fig.5 Typical leg of a jack-up platform

图6 撑管端部边界条件Fig.6 Boundary conditions at the brace ends
焊缝处应力集中系数可由下式得到,即

式中:σHss和σn分别为热点应力和名义应力。按照管节点有关设计规范(如CIDECT[11]和IIW[12])规定,热点应力可通过线性外插得到焊趾处的应力,即

式中:σ1和σ2分别为距离焊趾0.4To处和1.4To处垂直于焊缝的应力,其中To是所计算管壁厚度。
名义应力与所施加外载荷以及管节点的几何形状参数有关,本文中轴向载荷作用下的名义应力可由下式得到:

式中:F 为轴向外载荷,d 是撑管外部直径,t 是撑管厚度。
1.4 有限元结果验证
目前,关于多平面DT 型管节点沿焊缝应力集中系数的实验测量数据还鲜有报道。因此,本文采用与前文所述多平面DT 型管节点相同的有限元分析方法计算T 型管节点的应力集中系数,并与参考文献[13]中的实验值进行比较。验证结果在表2 中给出,可知有限元结果与实验结果平均值之间的相对误差的最大值为-17.59%,该误差水平在工程实际应用中认为是可以接受的[14],证明了本文中有限元建模方法的有效性。

表2 有限元结果与实验测量结果[13]的对比(D=914 mm,τ=0.5,β=0.5,γ=14.3,α=5.0)Tab.2 FE results compared with published experimental results[13](D=914 mm,τ=0.5,β=0.5,γ=14.3,α=5.0)
2 几何参数对应力集中系数分布的影响
基于所建立的352 个多平面DT 型管节点模型的计算结果,研究各几何参数对焊缝周围应力分布规律的影响。参数β 对轴向载荷作用下DT 型管节点应力集中系数分布的影响如图7 所示。由图可知,弦管侧应力集中系数最大值出现在外部鞍点处(即φ=270°)。当β 较小(β=0.2)时,撑管侧的应力集中系数最大值出现在外部鞍点附近。当β 较大时(β≥0.4),撑管侧的应力集中系数最大值在外部鞍点。外部鞍点处应力集中系数最大值与内部鞍点处应力集中系数最大值的差值随着β 的增大而增大。当β达到一定值时,内部(φ=0°~180°)应力集中系数最大值向内部鞍点偏离。因此,β 不仅影响应力集中系数的大小,同时又影响应力分布形式。
参数γ 对应力集中系数分布的影响如图8 所示,发现γ 对冠点处的应力集中系数影响很小,而在鞍点附近应力集中系数随着γ 的变大而变大。当γ 较小时(γ=10),弦管侧最大应力集中系数在鞍点与冠点之间,当γ 较大时(γ≥18)弦管侧最大应力集中系数位于外部鞍点。此外,撑管侧应力集中系数最大值随着γ 的增大而增大。
参数τ 对应力集中系数分布的影响如图9 所示,弦管侧应力集中系数分布整体随着τ 的增大而逐渐增大。在撑管侧冠点的应力集中系数随着τ 的增大而减小,而撑管侧鞍点的应力集中系数最大值出现在τ=0.6 时。τ 对应力集中系数的大小有明显的影响,但是并不改变最大应力集中系数出现的位置。

图7 参数β 对DT 型管节点应力集中系数分布的影响(α=15,γ=18,τ=0.6,ω=105°)Fig.7 Effect of β on the SCFs for multi-planar DT-joints(α=15,γ=18,τ=0.6,ω=105°)


图8 参数γ 对DT 型管节点应力集中系数分布的影响(α=15,β=0.4,τ=0.6,ω=90°)Fig.8 Effect of γ on the SCFs for multi-planar DT-joints(α=15,β=0.4,τ=0.6,ω=90°)
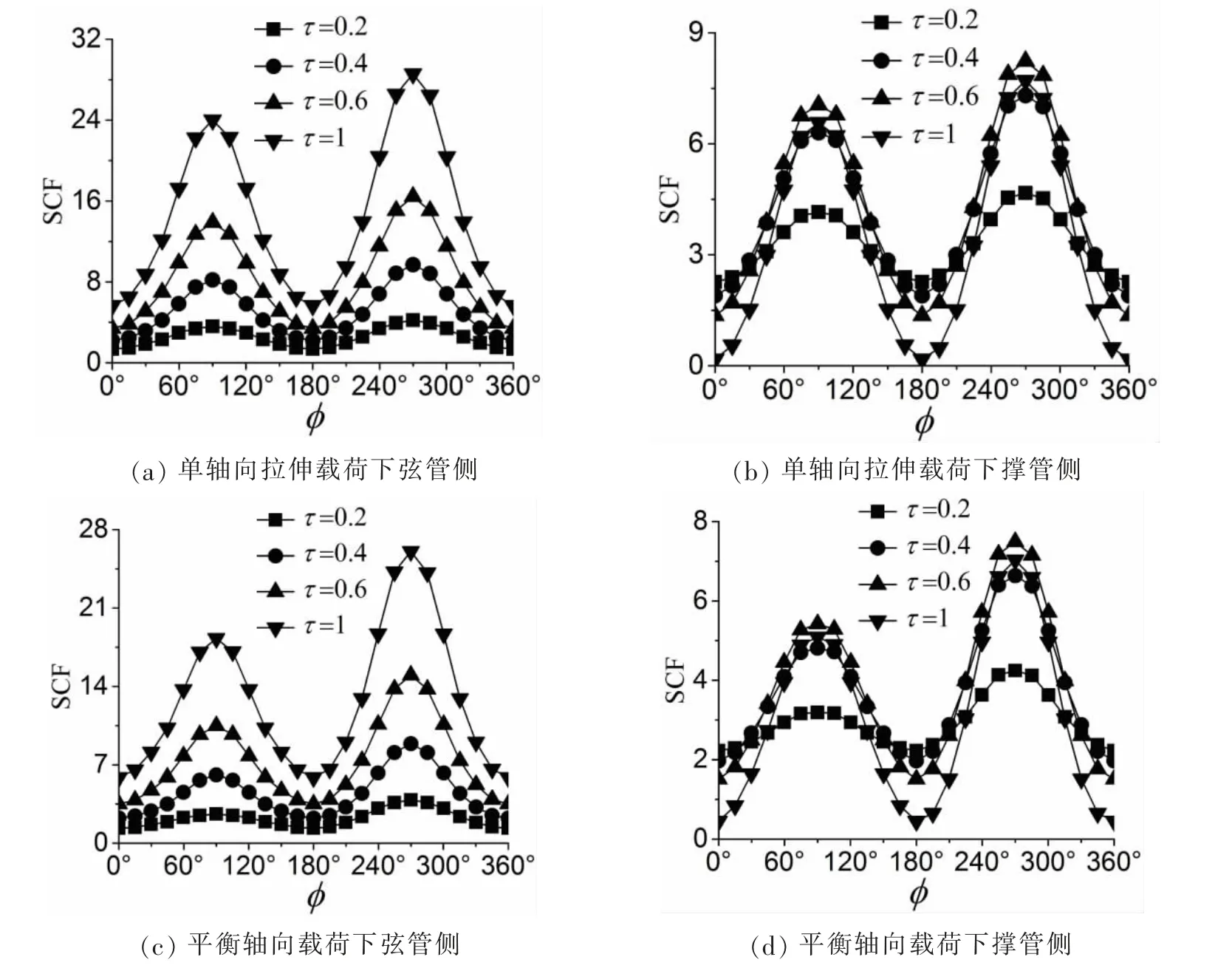
图9 参数τ 对DT 型管节点应力集中系数分布的影响(α=15,β=0.4,γ=24,ω=90°)Fig.9 Effect of τ on the SCFs for multi-planar DT-joints(α=15,β=0.4,γ=24,ω=90°)
如图10 所示,对于受单轴向拉伸载荷作用的管节点,当ω≤120°时弦管侧和撑管侧鞍点处应力集中系数随着ω 的增大而变大,而冠点处应力集中系数不受影响;当ω≥135°时,应力集中系数分布趋于稳定。对于受平衡轴向载荷作用的管节点,在鞍点处随着ω 的增大应力集中系数增大,而冠点处应力集中系数变化很小。
通过以上参数分析发现:轴向力作用下多平面DT 型管节点焊缝周围应力分布规律受到几何参数β、γ、τ 和ω 的影响,在这些几何参数的影响下焊缝处最大应力点位置并不确定,它可能位于冠点处也可能位于鞍点处,还可以位于冠点和鞍点之间任意一个位置处。

图10 参数ω 对DT 型管节点应力集中系数分布的影响(α=15,β=0.4,γ=24,τ=0.6)Fig.10 Effect of ω on the SCFs for multi-planar DT-joints(α=15,β=0.4,γ=24,τ=0.6)
3 应力集中系数参数公式拟合
基于上述有限元分析结果,采用双步回归分析方法建立轴向载荷下多平面DT 型管节点应力集中系数分布的参数公式。第一步,采用基于三角函数的离散型最小二乘法[15]拟合每个管节点沿焊缝应力集中系数参数方程,即

这里令n=5,采用MATLAB 软件中的非线性回归函数“nlinfit”进行非线性回归,分别得到每个管节点对应的a0、ak和bk的值。在求得的ak和bk的值中会出现令所有ak和bk都非常小的k 值,忽略上述ak和bk极小的情况进而得到应力集中系数参数公式的简化形式。第二步,采用多项式回归方法确定a0、ak和bk与管节点几何参数(β、γ、τ 和ω)之间的关系,a0、ak和bk统一记为Cp。

式中:q 为第一步中简化后a0、ak和bk的总项数,cijkl为待求系数,m 为自变量个数也是自变量最高次幂。以公式(6)作为拟合函数,采用MATLAB 中的交互式逐步回归函数“stepwise”进行非线性回归分析并在分析过程中去掉小于10-4的系数以简化公式,最终确定应力集中系数参数公式,具体见附录A。
为了检验拟合公式的准确性,采用两种常用于评价管节点应力集中系数拟合水平的相对误差形式[3]。第一种相对误差基于沿焊缝的最大应力集中系数,即:

式中:SCFEq,max和SCFFE,max分别是由参数公式和有限元分析得到的应力集中系数最大值。第二种相对误差采用沿焊缝的应力集中系数分布,即

式中:N 是某管节点模型沿焊缝线上提取有限元结果的点数,SCFEq(i )和SCFFE(i )分别是由参数方程和有限元分析得到的在第i 个节点对应的应力集中系数。
由于篇幅所限,这儿仅列出单轴向拉伸载荷下多平面DT 型管节点沿弦管侧焊缝的应力集中系数参数公式的误差分析结果,如图11 所示。可知,所拟合的参数公式与有限元结果的相对误差均小于20%,认为精度可满足实际工程需要[14]。
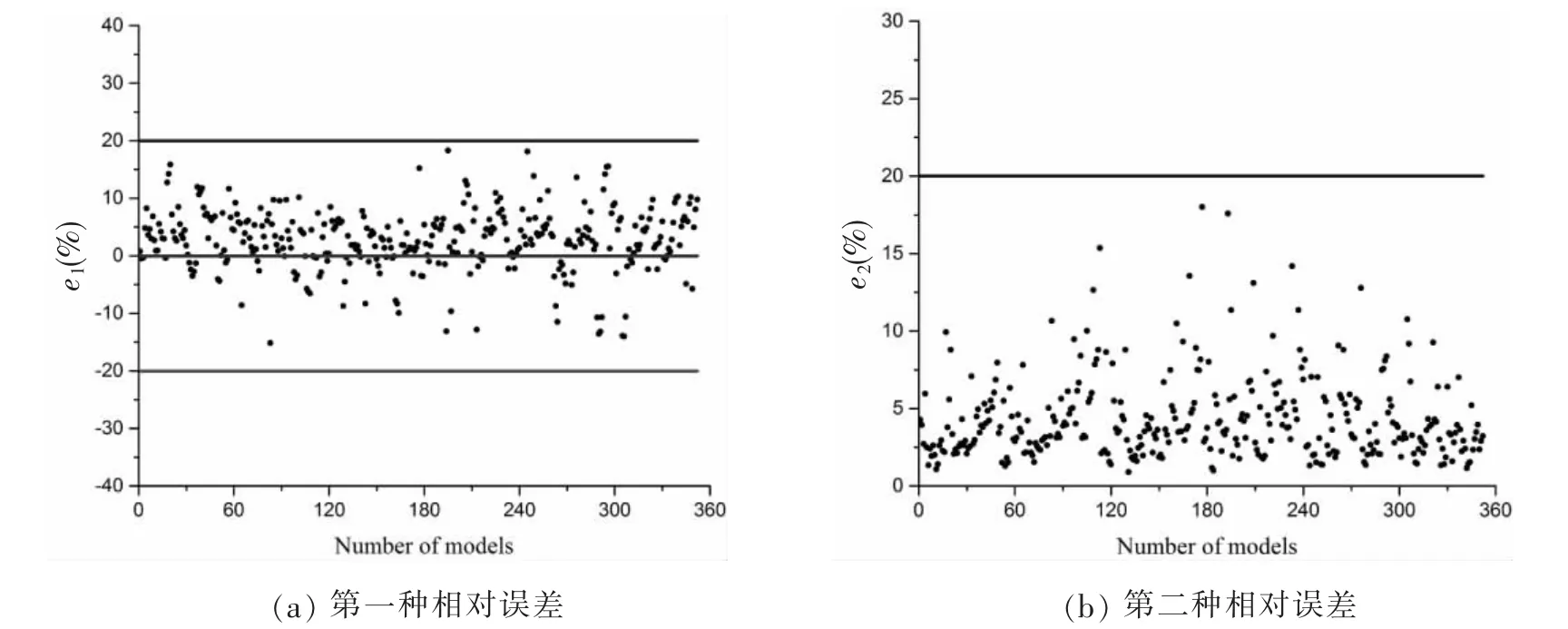
图11 单轴向拉伸载荷下DT 型管节点沿弦管侧焊缝的应力集中系数参数方程分叉分析Fig.11 Error analysis of the proposed equation for chord side of DT-joints under single axial loading
4 结 论
本文采用有限元方法分析了轴向载荷作用下多平面DT 型管节点焊缝周围的应力分布规律,提出一组新的应力集中系数参数公式,并得出如下结论:
(1)多平面DT 型管节点的几何参数(β,γ,τ 和ω)对沿焊缝应力集中系数分布规律的影响各不相同。β 不仅影响应力集中系数的大小,而且影响应力分布形式;在鞍点附近应力集中系数随着γ 的增大而增大;τ 对弦管和撑管侧应力集中系数的影响不同;ω 主要影响鞍点附近应力集中系数的大小。
(2)本文采用的双步回归方法对于管节点应力分布的拟合具有较好的效果。
(3)通过误差分析验证了所提出的多平面DT 型管节点应力集中参数公式的有效性,今后有望应用于海工结构设计以及疲劳强度分析,可避免工作量繁重的有限元建模工作。
附录A:多平面DT 型管节点沿焊缝的应力集中系数参数公式
A.1 单轴向拉伸载荷下沿弦管侧焊缝的应力集中系数参数公式:

式中:

A.2 单轴向拉伸载荷下沿撑管侧焊缝的应力集中系数参数公式:

式中:


A.3 平衡轴向拉伸载荷下沿弦管侧焊缝的应力集中系数参数公式:

式中:


A.4 平衡轴向拉伸载荷下沿撑管侧焊缝的应力集中系数参数公式:

式中:




