关于简谐运动微分方程的结论及其应用

郑 金

(凌源市职教中心 辽宁 朝阳 122500)

简谐运动的位移、速度、加速度等物理量都按正弦型函数变化；在LC回路的等幅振荡过程中，电容器极板上的电荷量、电路中的电流、电容器储存的电场能、线圈储存的磁场能等物理量都按正弦型函数变化.这些物理量都满足二阶齐次微分方程.反之，只要推导出某一物理量满足的二阶齐次微分方程，就可判断该物理量按正弦型函数变化，而且能够得出周期性变化的角频率以及方程的通解即函数关系式.

1 结论归纳

对于做简谐运动的弹簧振子，若以平衡位置为坐标原点，考虑到振动质点受到的回复力的方向总是跟振动位移的方向相反，则由牛顿第二定律可知回复力的大小为

由此得

这是振动位移所满足的二阶齐次微分方程，而简谐运动的位移图像为正弦(或余弦)曲线，表明振动位移是正弦型函数，一般关系式为

x=Asin(ωt+φ)

所以二阶微分方程的通解为

x=Asin(ωt+φ)

由此可得到关于简谐运动微分方程的一个数学结论.

结论:物体做简谐运动的位移y所满足的二阶齐次微分方程为

其通解为

y=Asin(ωt+φ)

(1)

等价式为

y=asinωt+bcosωt

(2)

式中的ω为简谐运动的角频率.

对于非齐次微分方程

可变形为齐次微分方程

令

可得

其通解为

Y=Asin(ωt+φ)

可知

(3)

即为

(4)

上述结论在高等数学中有严格的推导过程.若直接利用结论来解答有关物理问题，可避免复杂的数学积分演算过程，化繁为简.而把各种相关问题统一应用结论进行求解，有助于深刻理解物理问题的本质，拓展解题思路.

2 结论应用

简谐运动微分方程在物理问题研究和赛题解答方面可简化推导过程.对于有关复摆或非理想单摆的简谐运动以及LC电路电磁振荡的周期多大、某些物理量如何变化等问题，带电质点在恒力与洛伦兹力共同作用下的旋轮线运动以及弹簧复振子在恒力作用下周期性运动的竞赛题，有时需根据物理规律推导出二阶微分方程的标准形式，直接得出角频率，即可求出周期，再由其通解函数式和初始条件求出某些物理量的变化规律.下面以电磁振荡电路为例进行分析.

【例1】如图1所示，理想的LC回路，电容器带电荷量为qm，当闭合开关后，电容器极板上的电荷量以及电路中的电流都将发生周期性变化.试推导电容器极板剩余的电荷量及电流的变化规律.

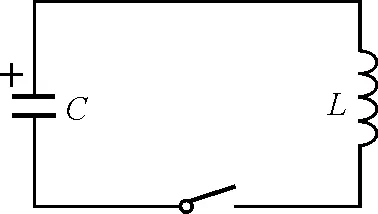
图1 例1题图

解析：设某时刻电容器处于放电状态，放电荷量为q，则电容器中剩余的电荷量为

Q=qm-q

可知放电电流为

由于电流逐渐增加，可知线圈的自感电动势方向与电流方向相反，其大小为

电容器两端的电势差大小为

其方向与电流方向相同，不计线圈和导线的电阻，由基尔霍夫定律列出回路电压方程为

uC-EL=0

联立以上方程可得电容器所带电荷量的微分方程为

令

得

可知其通解为

Q=qmsin(ωt+φ)

利用初始条件

t=0Q=qm

可得

还有一种解法，设电容器极板剩余的电荷量为q，对放电电荷量取导数可得放电电流大小为

由于放电电流逐渐增大，则自感电动势方向与电流方向相反，由于不计电阻，可知电容器的电势差与线圈的自感电动势大小相等，即

可得

点评：要注意电容器极板所带的电荷量与放出的电荷量的区别，而电流是对电路中变化的电荷量即电容器放出的电荷量而言的.微分方程中的电荷量是指电容器所带的电荷量，而不是放出的电荷量.如果利用通解

y=asinωt+bcosωt

也可得到相同的结果.

【例2】如图2所示，LC串联电路与直流稳压电源串联，闭合开关后，电路中的电流及电容器极板上的电荷量将如何变化？

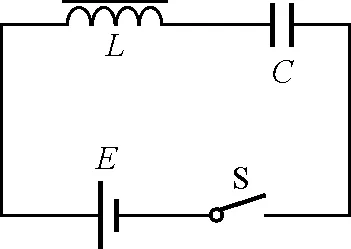
图2 例2题图

解析：闭合开关后，设电容器充电荷量为q，则两端电势差的大小为

由于充电电流增大，则线圈产生的自感电动势方向与电流方向相反，其大小为

由基尔霍夫电压定律列出回路电压方程为

uL+uC=E

联立各式得

两边取导数得

令

得

则通解为

i=imsin(ωt+φ)

下面分别求出φ和im.

利用初始条件

t=0i=0

可得

φ=0

所以

i=imsinωt

两边取导数得

考虑到电压方程为

利用t=0，uC=0,得

所以

还有一种解法，即推导出关于充电荷量的二阶微分方程

属于非齐次方程，利用其通解和电荷量的初始条件可求得电荷量的变化规律，然后取导数即得电流的变化规律.

点评:对于电路中含有直流电源的LC振荡电路，电容器极板上的电荷量并非按正弦型函数规律变化.还要特别注意t=0不是指开关闭合之前瞬时，而是指开关刚闭合瞬时.在求解im时，需对电流的表达式求出导函数式，不但要结合初始条件，还要利用回路电压方程.

在应用基尔霍夫电压定律列方程时，要注意规定正方向.可选择回路中电流的方向为正方向，以便确定方程中各物理量的正负，但首先要判断线圈的自感电动势的方向.

解题关键是推导出某个物理量满足的二阶微分方程的标准形式.可有两种推导方式，其一是利用二阶导数关系的物理量，如加速度等于位移的二阶导数，角加速度等于角位移的二阶导数，自感电动势跟电荷量的二阶导数成正比；其二是对一阶微分方程两边取导数.