基于STEM教育理念的“力的分解”教学设计
何晓萍
(浙江金华第一中学 浙江 金华 321015)
1986年,美国国家科学委员会在《尼尔报告》中提出“科学、数学、工程和技术集成”的纲领性建议,提倡开展STEM教育,培养复合型人才.STEM这一词汇是科学(Science)、技术(Technology)、工程(Engineering)和数学(Mathematics)4门学科的简称,但STEM教育并不是科学、技术、工程和数学教育的简单叠加,而是要将4门学科的内容进行组合形成一个有机的整体,得以更好地培养学生的创新精神与实践能力.
物理作为自然科学中最重要的一门学科,与技术、工程和数学等学科本身就有着密不可分的关系.因此,高中物理的课堂教学也应该将知识情景化,通过情景让学生获得尽可能多的体验,让学生学会利用科学、技术、工程或数学等学科相互关联的知识解决问题,提高学生的STEM素养.
下面以“力的分解”这一节课为例,谈谈自己对培养学生STEM素养的理解.
1 引入新课
新课的引入环节是每位一线教师高度重视的,正所谓“好的开始是成功的一半”,在讲授“力的分解”一节课时,笔者是这样引入的.
情境1:央视CCTV-2《是真的吗?》栏目有一期节目中提到,用尽全力也拉不直一根晾衣服的绳?是真的吗?请两位学生现场体验(图1),其他学生仔细观察.

图1 学生拉晾衣绳情景图
STEM素养目标:学生通过趣味实验体会到科学的魅力,更加想探究晾衣绳拉不直的真相.同时也为后面环节提供了分解实例,并应用于生活中缆车钢索、刀刃、拉链头等的技术设计.
2 力的分解
情境2:通过分析晾衣绳拉力的作用效果得出合力与分力的等效替代关系,提出力的分解的概念并复习平行四边形定则.接着每个学生在一张透明胶片上对同一个已知力进行分解,最后将几张胶片重叠(图2),看到一个已知力的分解可以画多个平行四边形,分解的方法并不唯一.
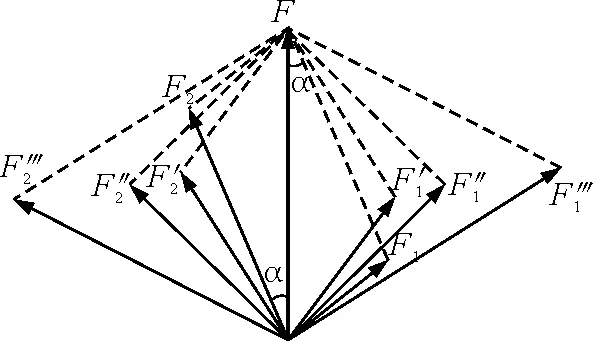
图2 胶片显示力的分解
STEM素养目标:学生在画平行四边形的过程中,既锻炼了动手能力,又进一步深刻地体会数学与物理的紧密联系,这也为部分将来从事技术、工程设计工作的学生打下良好的基础.通过动手结合观察重叠在一起的胶片,学生深入思考一个已知力的分解方法为何不是唯一的,最后找到分力的方向不确定这一原因.这也为后面实例中确定分力的方向作好了铺垫.
3 分解实例
3.1 “晾衣” 模型
(1)求解分力
情境3:如图3所示,将合力F沿两绳子方向分解,两分力的大小和方向都确定,可以用什么方法求解分力的大小?
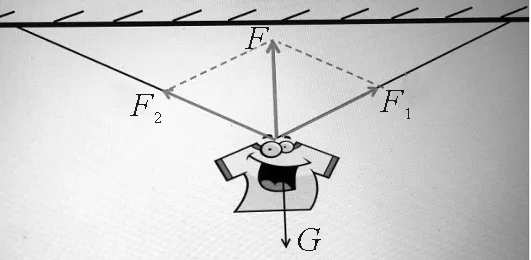
图3 力的分解示意图
首先可以用作图法,选择合适的标度,根据平行四边形画出合力与分力的图示,通过测量长度比例计算分力的大小;其次可以利用计算法,如图4所示,两分力与合力的夹角均为θ,画出另一条对角线找到直角三角形,就可以利用三角函数求得分力
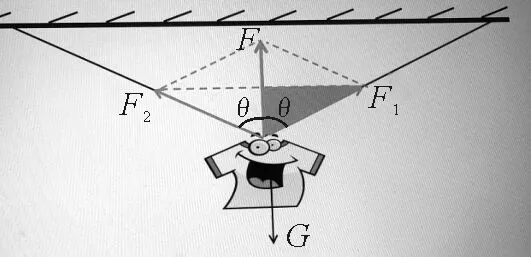
图4 构建直角三角形
如果角度θ不便测量,是否有其他办法计算cosθ?如图5所示,由两绳构成的等腰三角形中,合力F所在直线将该三角形分为两个直角三角形,F所在的直角边长H与单根绳长L的比值即为cosθ,因此
接着再让两个学生根据设计的方案进行实验(图6),测量H和L的长度,计算得到分力约为合力的5倍.
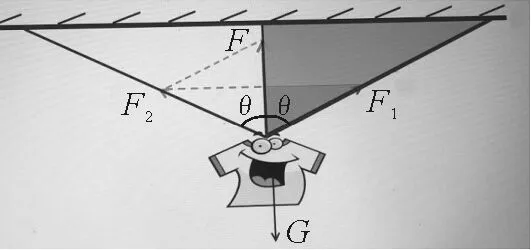
图5 相似三角形

图6 分力求解情景
STEM素养目标:学生在这一环节需要进行大量的思维活动,学会用数学的方法分析具体问题;学会设计实验方案,将难以测量的角度转换为长度;最后将数学、科学与技术有机结合,真正解决实际问题.
(2)生活中的应用
情境4:通过前面计算发现分力可以远大于合力,正因为如此,拉力随着两绳夹角的增大而增大,若要绳子拉直即夹角达到180°,绳子的拉力要趋于无穷大,显然这是不可能的,这也不是我们希望的.与晾衣绳类似的是缆车钢索,如图7(a)所示,为安全起见钢索不能拉得太直.但是在很多时候我们希望小力分解后能获得大力,比如刀刃、石拱桥、拉链头都是将小力分解到两个夹角接近180°的两个方向获得很大的分力,如图7(b)、(c)、(d)所示,可谓是“小力分解得大力,四两也能拨千斤”!
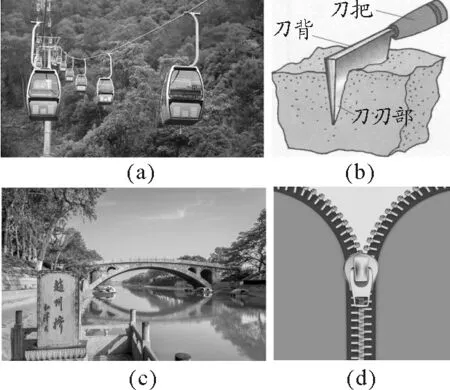
图7 力的分解实例
STEM素养目标:学生在这些生活中随处可见的例子中体会到科学的力量与人类的智慧.小到刀刃、拉链头,大到拱桥,都需要仔细考量、精心设计.这也是培养学生工程与技术素养的最好案例.
3.2 塔吊“支架” 模型
情境5:塔吊是建筑工地上常见的搬运工具,学生在本节课动手亲自体验塔吊模型中重物拉力所产生的作用效果,对合力进行分解,如图8所示.在平行四边形中找到直角三角形,利用三角函数可求得
将F2平移可以得到图9所示的合力与分力构成的矢量三角形,并且与位移的矢量三角形进行类比,让学生对矢量三角形中体现的合力与分力的大小、方向关系有更加深刻的理解.
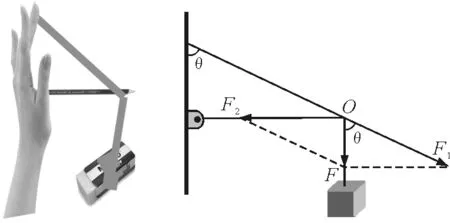
图8 塔吊支架模型图解
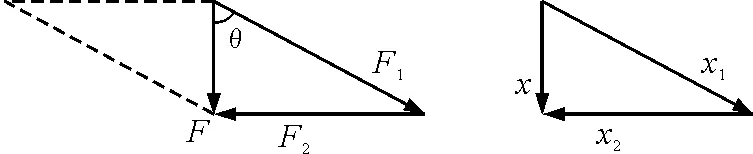
图9 矢量三角形示意图
STEM素养目标:学生动手搭建支架的过程中,要通过调整横杆与掌心的接触点来使整个支架处于平衡状态,这是科学知识指导下的工程、技术体验.学生通过手指和掌心真实地感受到力的作用效果,确定分力的方向,最后通过矢量三角形求解分力的大小,这是科学与数学的完美结合,物理中矢量与数学中的向量本就是同一个概念.
3.3 “爬山” 模型
情境6:每个人都有过爬山的体验,自然都知道山路越陡越难行,可以从力的角度解释一下这个问题吗?
先把山坡简化为斜面,然后通过简单的软木板斜面实验让学生看到重力所产生的沿斜面向下滑和垂直斜面向下压斜面的效果.最后对重力进行分解(图10)并求解出分力
G1=GcosθG2=Gsinθ
根据表达式可知斜面倾角θ越大,重力沿斜面向下的分力G2就越大,要想沿斜面向上运动自然就越困难.对情景6中的应用起到过渡作用.
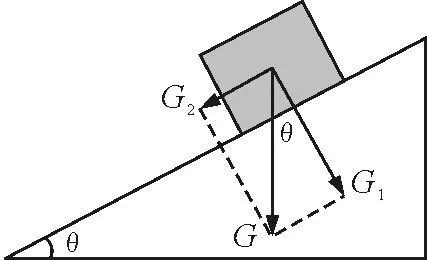
图10 将山坡简化为斜面分解重力
情境7:考虑到减小上坡时重力斜向下的分力,在道路设计时倾角不宜过大,因此有了蜿蜒曲折的盘山公路,如图11(a)所示.架在宽阔的江河上的大桥也都有一段长长的引桥,如图11(b)所示的黄石长江大桥引桥长约840 m,高约24 m.而图11(c)所示的是日本的江岛大桥.看上去简直让人惊叹,上行时每前进100 m约升高6 m.看似惊人的大桥其实并不那么陡峭!我们可以假设两座大桥的倾角分别为α和β,因此
由于sinα和sinβ都极小,我们可以认为
sinα≈α=0.03 sinβ≈β=0.06
最后将弧度单位转化为角度可得
α≈1.72°β≈3.44°
所以引桥倾角的设计都是要符合安全要求的,江岛大桥并没有图片中所显示的那么陡峭.

图11 斜面上重力的作用在山路和桥梁设计上的体现
STEM素养目标:以上两个情景主要涉及斜面上重力作用效果的问题,不管是爬山还是过桥,都是学生非常熟悉的情景,他们都有过多次的体验.在科学原理的指导下对山路和桥梁进行科学地设计,才能符合安全标准.对两座大桥引桥倾角进行计算时,用到了近似的数学思想,学生学会了通过分析计算来辨别信息的真伪,成为真正的STEM人才.
4 反思总结
本节教学设计基于学生的生活经验,让物理从生活中来,又到生活中去.学生通过各种体验学会了对力进行分解,并且能够计算出分力的大小,具体的分解流程如图12所示.
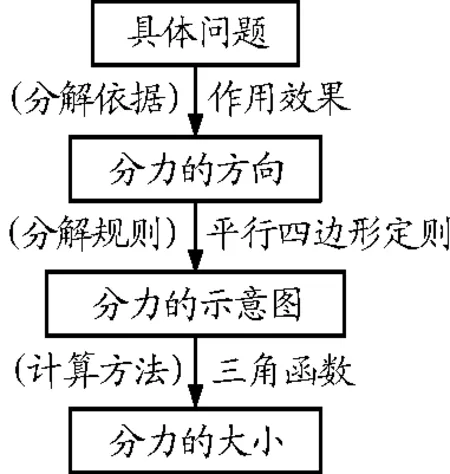
图12 力的分解流程图
本节课的每个环节都在尽力整合科学、数学、工程和技术这4门学科,每一个规律的得出都是完美的数理结合,每一个生活的应用都是绝伦的工程设计.当今社会最需要的就是人才,而STEM教育是培养复合型人才的重要途径.所以,作为基础教育工作者应该更新教育理念,变革课堂模式,培养综合人才.

