大跨度连续刚构桥在地震、波浪作用下的动力响应
柳春光,王晓晓
(大连理工大学 建设工程学部, 辽宁 大连 116024)
伴随着我国的交通事业的迅猛发展,在西部山区修建的入水深度较大的大跨度连续刚构桥梁越来越多,这些桥梁在建造和使用期间要承受地震、波浪、水流、风等自然环境荷载作用,这些作用均以动力荷载的形式作用于结构之上。地震作用下,结构的运动会引起结构周围水体的辐射波浪运动,由于结构与水的相对运动,结构的水下部分会受到地震动水压力的作用。地震动水压力不仅会影响结构的振动特性,还会影响结构在地震作用下的动力响应[1]。随着桥梁下部结构入水深度增大,波浪对桥梁结构的动力作用变得不容忽视,尤其在桥梁的自振频率和波浪运动的频率接近时,两者将产生共振。至今虽然我国尚未发生因台风和波浪作用导致跨海桥梁破坏的安全事故,但因为跨海及深水桥梁的桥墩和基础长时间在复杂且多变的海洋工况中,在持续的且高强度的波流力作用下,桥梁的墩柱与基础等下部结构须具有足够的强度与刚度,在设计时这些都是必须要考虑的因素。
1 地震、波浪作用的研究现状
1.1 地震动水压力的研究现状
针对在地震、波浪作用下水中结构物的动力响应问题国内外学者进行了很多研究,并取得了一定的成果。对于地震动水效应的研究,目前常采用的方法有附加质量法和有限元法,上歧宪三等[2]在1965年对附加质量模型进行了早期研究。Ronald[3]对有限水深中垂直圆柱体的动水附加质量和附加阻尼进行了研究。赖伟[4]根据线性福射波浪理论,分别采用解析法和有限元法结合的方法提出了求解圆截面桥墩动水压力半解析半数值的方法,讨论了矩形桥墩和承台动水压力的近似计算方法。高学奎[5]在Morison方程的基础上,采用附加质量考虑水的影响,分析了地震动水压力对深水桥墩动力响应的影响。杨万里[6]综合流体单元法和简化辐射波浪法的优势提出了一种计算外域水动水压力的混合法,基于该方法得出了正方形桥墩和矩形桥墩外域水附加质量的表达式,由此所得外域水的附加质量表达式非常简洁,进而使得计算效率提高。刘振宇[7]依据线性波浪理论和线性波浪辐射理论建立了求解圆形桥墩内域水、矩形桥墩内外域水动水附加质量的方法,这使得动水附加质量的计算从外域水延伸至内域水,并从圆形桥墩发展到矩形桥墩。李忠献[8]研究了桥墩为实体墩的深水桥在地震、波浪联合作用下的动力响应。
1.2 波浪作用的研究现状
对于波浪力的研究开展也比较早,最早用来计算立于水中刚性桩柱的波浪力常采用的Morison方程[9]以及许多学者对结构物在波浪作用下的响应的研究,取得一些成果。陈国兴[10]在桥墩上施加分布力形式的波浪力,研究了波流对群桩基础桥墩在地震作用下的影响。朱照清等[11]介绍和总结了Morison方程在计算波浪力时所涉及的研究成果。李帅帅等[12]用数学理论导出了不同波浪荷载形式下波浪作用的表达式,并对桥墩码头结构在波浪荷载作用下的动力响应进行了分析。吴安杰等[13]基于非线性Morison方程,研究了桩-承台-桥墩结构在地震、波流多环境荷载共同作用下的动力响应。林曾等[14]建立了深水桥墩在波浪作用下的地震响应分析的方法,并以典型的实体圆形桥墩为算例,研究了仅在地震作用下、仅在波浪作用下、波浪联合作用下桥墩的动力响应。
在桥梁工程领域,目前大多数学者都是将桥墩从整个桥梁结构中隔离出来,单独进行桥墩在地震波浪作用下的动力响应研究,关于整桥结构在地震波浪作用下的动力响应的研究相对较少,尤其在采用空心桥墩的桥梁结构这方面的研究屈指可数。鉴于此,本文采用杨万里[6]所提到的方法计算桥墩内外域水地震动水压力、采用《海港水文规范》[15](JTS 145-2—2013)中提到的方法计算波浪作用,对矩形空心墩的大跨度连续刚构桥梁在地震、波浪作用下的动力响应进行研究。
2 连续刚构桥梁地震、波浪作用下的动力响应分析方法
为考虑地震作用下桥墩动水力的作用,采用辐射波浪法[6],即假设流体是理想流体,无黏无旋且不可压缩。将结构运动引起的辐射波考虑为势波。在波浪作有势运动时,求得波动水域中的速度势,之后求得波动场中各点的速度、波压。对流体与结构界面上波压沿着界面积分,可得到水体波动对结构产生的压力,基于辐射波浪法的墩水耦合作用计算模型见图1。

(a) 简化模型 (b) 计算模型
图1基于辐射波浪法的墩水-耦合作用计算模型
文献[6]基于辐射波浪理论,不考虑动水压力项中阻尼的影响,得矩形桥墩考虑内域水动水压力时结构的运动微分方程如下:
(1)

(2)
(3)
(4)
(5)

文献[5]第五章基于流体单元法和辐射波浪法提出了一种新的计算方法混合法,应用混合法求出了矩形桥墩外域水动水附加质量,并与流体单元法和简化辐射波浪法进行了对比,验证混合法计算在精度上能满足工程需要。矩形桥墩考虑外域水动水压力时结构的运动微分方程(6)如下:
(6)
其中:
(7)
Mwato=ρπD2/4
(8)
(9)
(10)
Srec(lab,D,H)=
(11)
lab>1
(12)
(13)
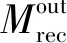
当同时考虑矩形桥墩内外域水共同作用,不考虑自由表面波,忽略阻尼项作用,结构运动微分方程为:
(14)
其中Min为基于简化的辐射波浪法得到的内域水的附加质量;Mout为基于混合法得到的外域水的附加质量。
上诉方法在实现过程中,仅需在传统桥梁抗震有限元分析模型中桥墩水下部分施加Mass 21单元以考虑附加质量影响,就能考虑地震动过程中水对结构的影响[4]。
针对波浪作用,本文采用规范[15]中提到的方法进行计算波浪作用,并将计算得到的波浪作用时程以分布力的形式施加与结构水下部分的节点上,进行动力时程分析。
3 工程概况和计算模型的建立
3.1 有限元模型的建立
某大跨连续刚构桥,桥面宽度13 m,主跨为220 m,两边跨为120 m,桥梁上部结构采用C60混凝土,下部桥墩结构采用C50混凝土。该桥主梁为单箱单室变截面混凝土连续梁,主跨跨中梁高4.5 m,刚构墩顶梁高14.5 m,箱梁自根部至跨中梁高呈1.8次抛物线变化;主跨跨中箱梁底板厚度为0.35 m,根部底板厚度为1.47 m,底板厚度呈1.8次抛物线变化。桥墩采用矩形空心墩,1#、4#桥墩墩高分别为81 m、88 m,墩底截面尺寸分别为6.02 m×9.22 m、6.20 m×9.40 m,壁厚为0.7 m、0.8 m、0.9 m分段阶梯型变化,桥墩沿高度方向在顺桥向和横桥向均按1∶80放坡;2#、3#主墩墩高172 m,墩底截面尺寸为13.01 m×12.73 m,墩顶截面尺寸为11 m×7 m,壁厚为0.7 m、0.8 m、0.9 m分段阶梯型变化,桥墩沿高度方向在顺桥向从某一高度开始按照1∶100放坡,在横桥向按照1∶60放坡。在正常蓄水位时,1#、4#桥墩入水深度分别为77 m、84 m,2#、3#桥墩入水深度为165 m,桥梁简化后的模型如图2所示。

图2连续刚构桥简化模型
为准确求得在地震和波浪作用下大跨度连续刚构桥梁的动力响应,以及桥墩形状对动水附加质量的影响,按实际尺寸建立主梁和各桥墩的有限元计算模型。
根据辐射波浪法的墩水耦合作用计算模型可知,在建立有限元模型时可采用三维梁单元单元进行模拟主梁和桥墩[4],在1#、4#墩顶施加Mass 21以考虑相邻跨简支梁的影响,2#、3#上部箱梁刚结,约束使1#、4#墩顶与连续刚构体系边跨端竖向自由度一致,纵横向可产生相对位移,桥墩底部均固结。桥梁有限元模型如图3。

图3连续刚构桥有限元模型
3.2 有水无水条件下桥梁动力特性的对比
结构动力特性是动力响应分析的基础,通过A有限元分析软件分析可知,有水无水情况下前五阶振型出现顺序一致,表1是该桥梁在不考虑水体和考虑水体时的前五阶频率及降低程度,以及振型描述。

表1 有水无水工况下连续刚构桥梁自振特性比较
由表1可看出,连续刚构桥梁横向、纵向和竖向刚度相比横向刚度为最小,在地震和波浪作用下将以横向振动为主,且从前五阶的自振频率来看,考虑与不考虑水体自振频率有明显的变化,例如,有水无水情况下一阶自振频率降低幅度为9.83%;连续刚构体系纵向反对称弯曲振动频率由0.245 69降低至0.212 56,减小幅度为13.48%;水体的存在对主梁对称横向弯曲振动影响很小,主梁对称横向弯曲振动频率考虑水体与不考虑水体时频率变化率为0.52%。同时由振型特性知水体对连续刚构桥梁的振型影响很小,是否考虑水体,前8阶振型出现顺序一致。
4 连续刚构桥梁动力响应分析
4.1 连续刚构桥梁在地震作用下的动力响应分析
对有水无水情况下的连续刚构桥有限元模型,采用El Centro(1940年,SN方向)波和汶川波(2008年,卧龙台站SN向),沿横桥向输入加速度峰值为0.2g的地震动进行地震作用模拟。桥梁在地震作用下关键节点的动力响应见表2,关键节点位移增幅见表3。
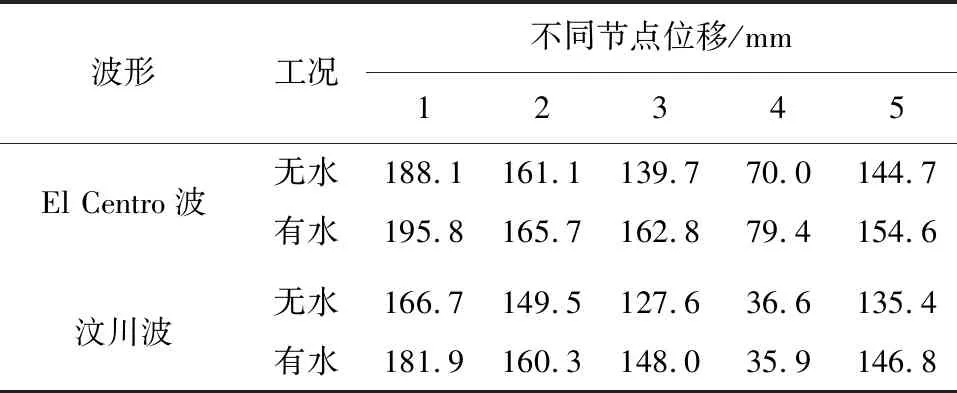
表2 地震作用下连续刚构桥梁关键节点处位移

表3 地震作用下连续刚构桥梁关键节点处位移增幅
图4、图5为El Centro波和汶川波作用下1#墩顶2#墩顶无水和正常蓄水位时的位移时程曲线。
由表2可知,水体的存在对各关键点位移极值的影响不一致。由图4和图5可以看出,水的存在仅影响了结构的响应极值,由于水的存在,使得极值出现的时间发生变化,结构的响应出现延迟。
由表3可知,El Centro波作用下,1#墩和2#墩顶的位移增幅分别为13.51%、6.89%,由于1#桥墩与桥梁上部结构仅约束竖向位移一致,而2#墩顶与桥梁上部结构为完全约束,并且2#墩的入水深度要远大于1#墩,故而可得水体对结构位移响应的影响不仅与墩顶和上部结构的约束条件有关还与桥墩的入水深度有关。

图4ElCentro波作用下4#点、5#点位移时程曲线

图5汶川波作用下4#点、5#点位移时程曲线
而在汶川波作用下1#墩和2#墩顶的位移增幅分别为-1.91%、8.42%,与El Centro波作用下关键节点位移增幅比较,可得水体对结构位移响应的影响也和输入的地震波有关。
1#墩顶和主梁简支端位移峰值和增幅均不一样,说明在地震作用下主梁简支端将在支座上产生相对滑动。
El Centro波作用下,中跨中点(3点)的位移增幅为16.49%,边跨中点(2点)的位移增幅为2.87%,水体的存在对连续刚构桥梁中跨中的影响比边跨跨中的影响要大,对汶川波有同样规律。
4.2 波浪作用动力响应分析
根据实际情况,考虑波浪沿横桥向作用于结构之上时连续刚构桥梁的动力响应。根据规范[15]计算波浪对墩柱的作用。桥梁在波浪作用下关键节点的动力响应如表4。波浪作用下1#、2#墩顶位移时程曲线见图6。
由表4和图6可以看出在波高相同的情况下,结构的位移响应和波浪周期有关,波浪3和波浪4作用下结构的位移响应较大,由于波浪3的频率为0.153 846 Hz≈0.154 Hz,波浪4频率为0.161 29 Hz≈0.161 Hz,结构基频为0.155 38 Hz≈0.155 Hz,和结构的频率很接近,所以使得该波浪工况下结构响应较大。而波浪1和波浪2的频率与结构频率不再相近,故而对结构的响应也较小,但也不容忽视。由图6可以看出4#点和5#点在波浪作用下的响应极值不同,这是由于4#点和5#点与桥梁上部体系约束形式和入水深度不一致,由此可知结构对波浪作用的响应和结构的约束形式及入水深度有关。
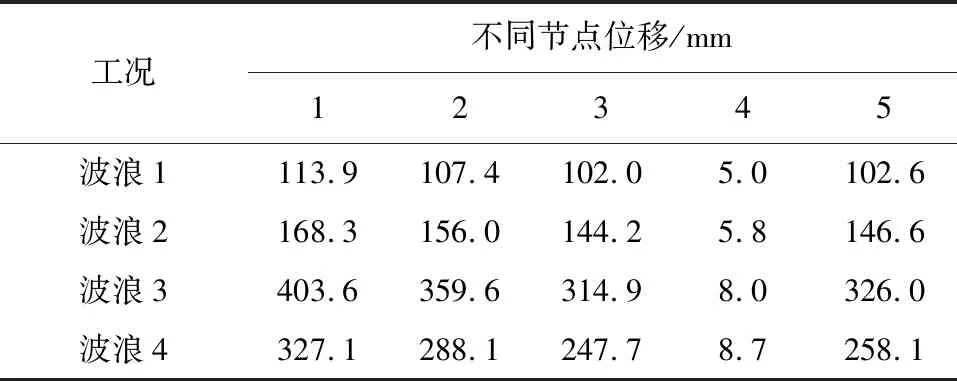
表4 波浪作用下连续刚构桥梁关键节点处位移
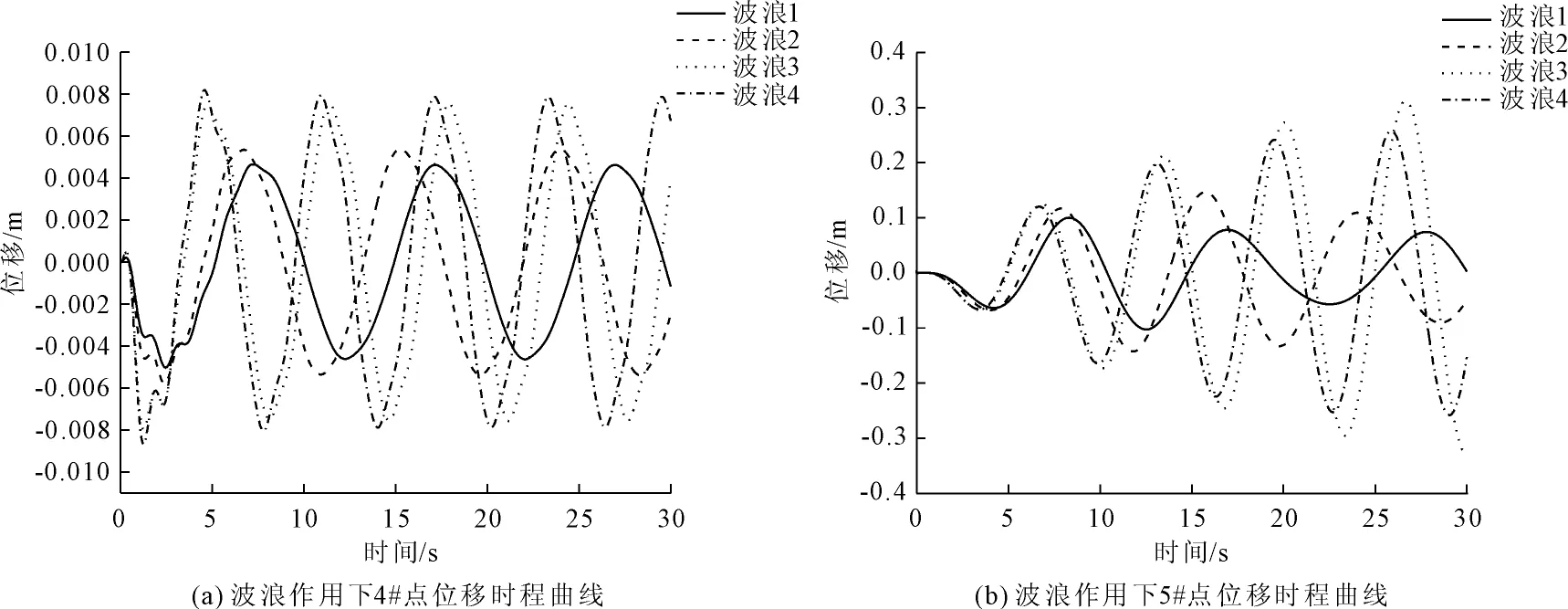
图6波浪作用下4#点、5#点位移时程曲线
对比表2和表4可知,地震作用比波浪1、波浪2作用下结构位移响应大,但是相比波浪3、波浪4作用下结构位移响应较小,故地震作用和波浪作用对结构动力响应的影响相比,不仅和输入的地震波加速度峰值有关也和波浪的周期有关。
实际工程中,相对地震作用而言,波浪作用是长期存在的外部荷载,虽然波流共同存在,会使得波浪周期改变,但在设计桥梁时,也应根据当地的水文资料,使得结构的频率避免与设计波浪频率相近,从而避免共振。
5 结 论
(1) 考虑水体存在对结构位移响应的影响和输入的地震波、结构的约束形式以及桥墩的入水深度均有关。地震作用下,考虑水体存在时,结构位移响应的最大增幅为16.5%,考虑水的存在是有必要的。
(2) 不能片面的去比较波浪作用和地震作用对结构响应的影响,波浪要素和输入地震波的加速度峰值会影响结构的响应,当波浪的频率和结构频率接近时,会使得结构出现共振现象,从而导致结构响应变大。
(3) 单独考虑地震和波浪的作用,忽略了地震波浪联合作用下,地震对波浪场的影响,进而使得桥墩周围水质点的运动频率不再是单纯波浪作用下的频率。因此应当更深层次的考虑地震波浪联合作用下结构的动力响应。

