基于先验信息约束的核磁共振数据反演新方法

金国文, 谢然红, 徐红军, 郭江峰, 高 伦

(1.中国石油大学(北京)油气资源与探测国家重点实验室,北京 102249; 2.中国石油大学(北京)地球探测与 信息技术北京市重点实验室,北京 102249; 3.中国石油勘探开发研究院,北京 100083)

核磁共振(NMR)测井直接测量地层孔隙流体信息,在流体识别、孔隙度计算和束缚水评价等方面具有独特优势[1-3]。NMR回波数据反演是NMR测井应用的基础,国内外学者提出了多种反演方法[4-8]。截断奇异值分解法[9-10]和Tikhonov正则化方法[11-13]是两种常用的核磁共振反演方法,其中Tikhonov正则化方法又包括模平滑、斜率平滑和曲率平滑方法。但总体而言,现有的反演方法对于NMRT2谱短弛豫组分的反演精度还有待提高。致密砂岩、页岩等非常规储层孔径小,在T2谱上反映为短弛豫组分居多,而反演结果的不准确则制约了核磁共振测井在非常规储层中的应用。积分变换方法的发展与应用为提高NMRT2谱短弛豫组分的反演精度提供了有效途径[14-17]。笔者将积分变换方法应用于核磁共振数据反演中,提出一种基于先验信息约束的NMR反演新方法(ILT+),并通过数值模拟和实际井资料处理验证新方法的有效性。

1 基于先验信息约束的NMR反演新方法

在完全极化的条件下,NMR测井采集的CPMG回波串幅度可用如下第一类Fredholm积分方程来表示:

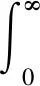
(1)

式中,b(t)为采集的NMR回波数据;exp(-t/T2)为核函数;T2为NMR横向弛豫时间;f(T2)为T2谱幅度;ε(t)为高斯白噪声。

公式(1)的离散矩阵形式为

Ap×qfq×1=bp×1.

(2)

其中

Aij=exp(-ti/T2,j);

fq×1=[f(T2,1),…,f(T2,q)]T;

bp×1=[b(t1)-ε(t1),…,b(tp)-ε(tp)]T;

i=1,…,p,j=1,…,q.

式中,p为回波个数;q为T2布点数。

方程(1)的求解通常采用Laplace逆变换(ILT),但核磁共振数据ILT是一个严重病态问题,噪声项导致解的扰动[18]。为了解决这一问题,通常采用正则化方法,求解如下目标函数:

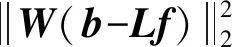
(3)

式中,W为权重矩阵;b为测量数据矩阵;L为系数矩阵;f为待反演T2谱的离散形式;α为正则化参数。

基于先验信息约束的NMR回波数据反演(ILT+),通过积分变换方法直接从NMR原始回波数据中提取先验信息作为约束条件来构建新的反演目标函数,具体为采用指数双曲正弦变换(ESHT)求取锥形区域面积(S),采用梅林变换(MT)求取T2的ω次幂的均值(T),最后求解目标函数得到更为准确的NMRT2谱。具体步骤如图1所示。

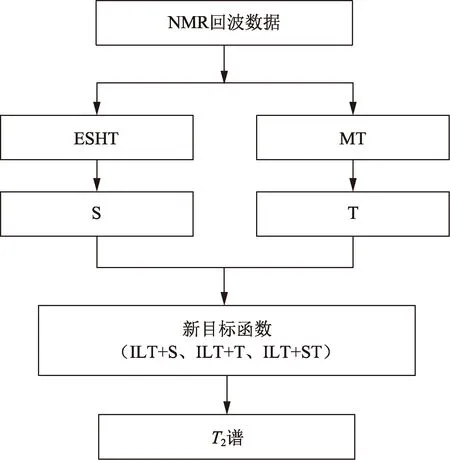
图1 ILT+反演方法流程Fig.1 Workflow of ILT+

1.1 指数双曲正弦变换求取锥形区域面积

传统方法中,用T2截止值(单一截止值或渐进截止值)在反演得到的T2谱上划分小孔隙和大孔隙,小于T2截止值的锥形区域面积对应束缚流体体积,大于T2截止值的锥形区域面积对应自由流体体积[19]。锥形区域面积可用如下公式计算:

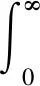
(4)

式中,S为锥形区域面积;TC为T2截止值(可通过经验或实验获得);K(T2,TC)为截止值函数,由于本文中采用渐进截止值,可用渐进阶跃函数近似。K(T2,TC)需要满足如下特定值条件:

K(T2,TC)|T2=0=0,

K(T2,TC)|T2=TC=n,

式中,n、m为设定值。如图2所示,实线为地层T2分布模型,虚线代表T2截止值为TC时对应的渐进阶跃函数,阴影部分为所求锥形区域面积。

假设K(T2,TC)对应的拉普拉斯逆变换函数k(t,TC)存在,即满足关系式

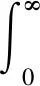
(5)

则将公式(5)代入公式(4)中,结合公式(1)推导可得

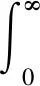
(6)

式中,I{b(t)}表示对b(t)作积分变换。由公式(6)可知,若可求得核函数k(t,TC)满足公式(5),则可直接通过对NMR原始数据作积分变换求取锥形区域面积。

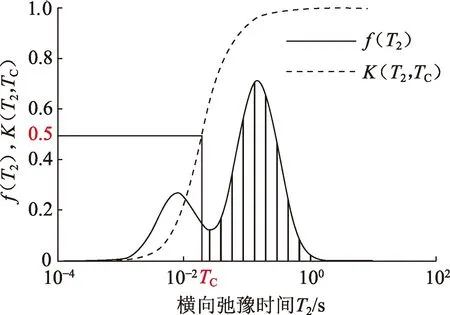
图2 地层T2分布模型和T2截止值 为TC时对应的渐进阶跃函数Fig.2 T2distributions and tapered heaviside function withT2cutoff value equalingTC

公式(6)离散形式为

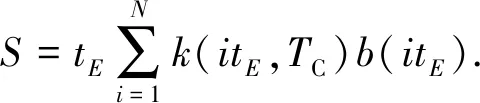
(7)

式中,tE为回波间隔;N为回波个数。进一步可得积分变换方法所求锥形区域面积对应的方差:

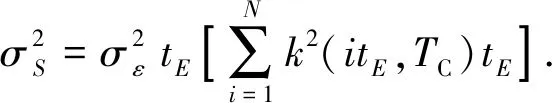
(8)

式中,σS为锥形区域面积标准差;σε为噪声标准差。由公式(8)可知,只有当核函数k(t,TC)满足平方可积,即能量E有限时:

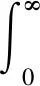
(9)

所求锥形区域面积对应方差才是有限的,此时通过积分变换求取锥形区域面积的方法才可行。

本文中选取的核函数为指数双曲正弦函数,由于原始双曲正弦函数不满足公式(9)能量有限原则,故增加指数衰减项,如下式所示:

k(t,TC)=λe-βtsh(αt).

(10)

式中,sh(αt)为双曲正弦函数;λ、β、α为未知参数;t为时间。

对公式(10)作拉普拉斯变换可得

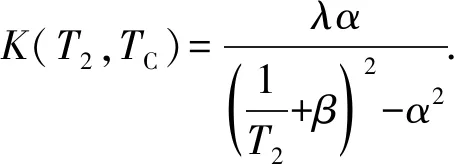
(11)

根据K(T2,TC)满足的特定值条件,计算得到各未知参数分别为

其中

通过数值模拟确定经验参数n=0.5,m=0.3。

由于所选核函数为指数双曲正弦函数,这里称通过该积分变换求取锥形区域面积的方法为指数双曲正弦变换法,简记为ESHT。图3显示了TC=33 ms时对应的拉普拉斯变换函数对。

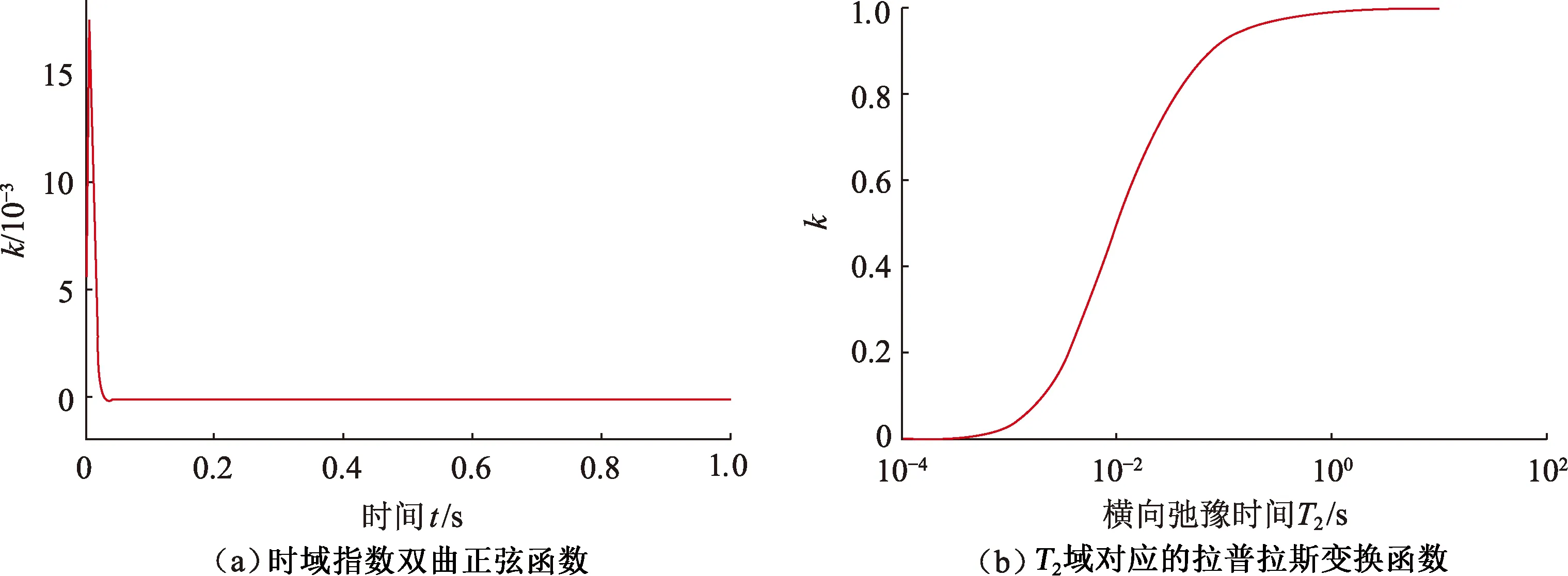
图3 指数双曲正弦变换在时域和T2域对应的函数形式Fig.3 Exponential hyperbolic sine transform in time domain andT2domain

1.2 梅林变换求取

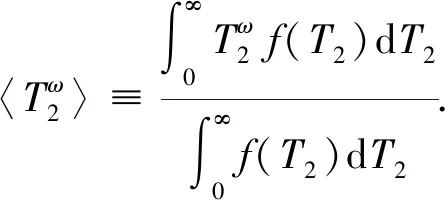
(12)

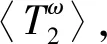
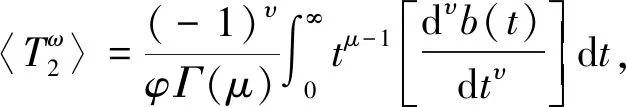
(13)

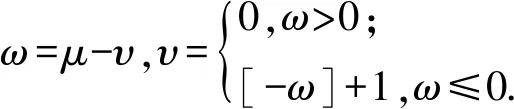
(14)

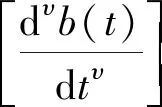
1.3 反演目标函数构建

将通过ESHT方法和MT方法从原始回波数据中提取的先验信息作为约束条件,添加到原反演方法目标函数公式(3)中,构建新反演方法的目标函数:

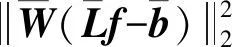
(15)

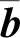
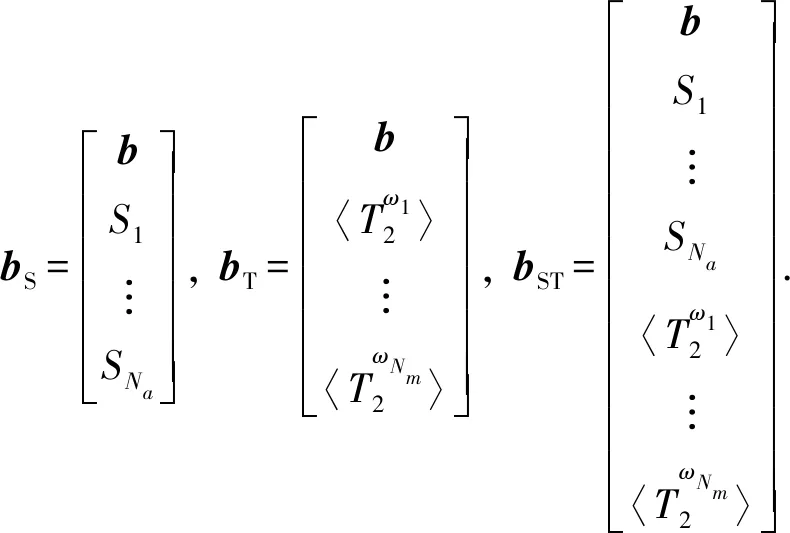
(16)

式中,Na为所选TC个数;Nm为所选ω个数。

(17)

式中,T2,min和T2,max分别为离散化的T2中的最小值和最大值。

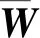
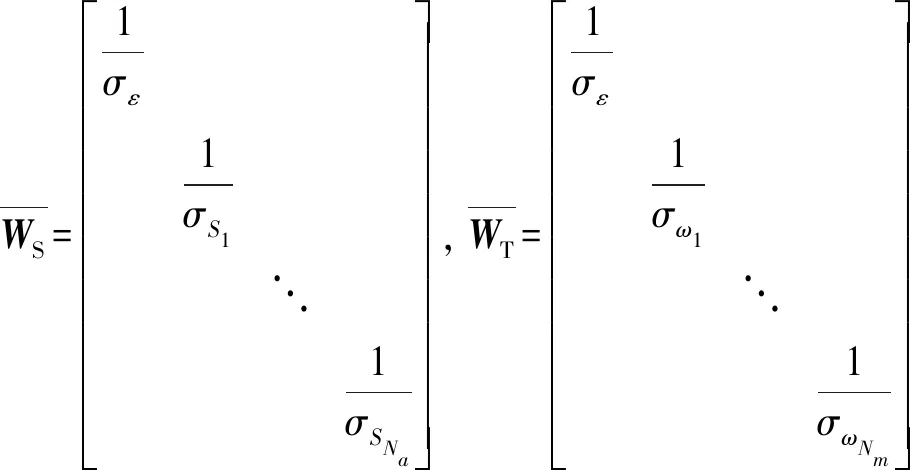
(18)

2 数值模拟结果分析

模拟两种具有双峰结构的T2分布地层模型,给定地层模型的孔隙度为10%,如图4所示,T2布点数为64,其中图4(a)为大孔占优T2分布地层模型,图4(b)为小孔占优T2分布地层模型,纵坐标φ为孔隙度。根据此地层模型正演合成回波间隔为0.2 ms,回波个数为5 000的回波串,并加入噪声水平为0.5 pu的高斯白噪声,正演结果如图5所示。

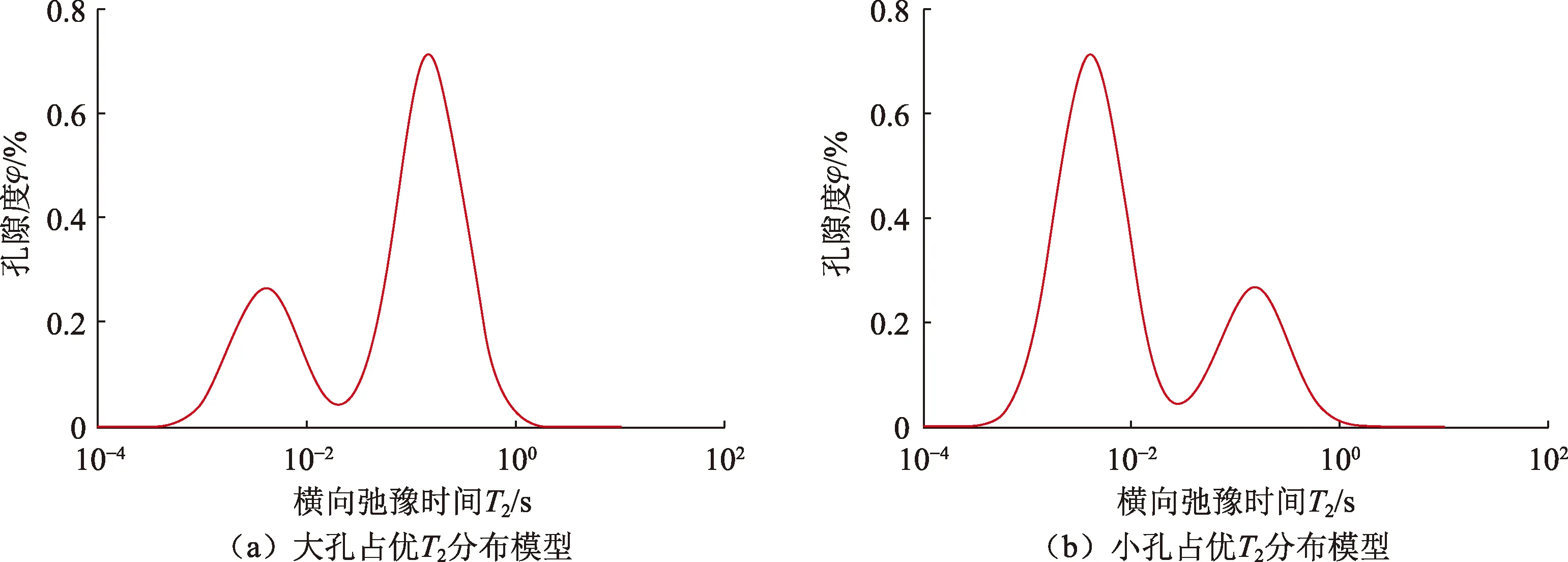
图4 大孔占优和小孔占优T2分布模型Fig.4 T2distributions with more macropore and more micropore

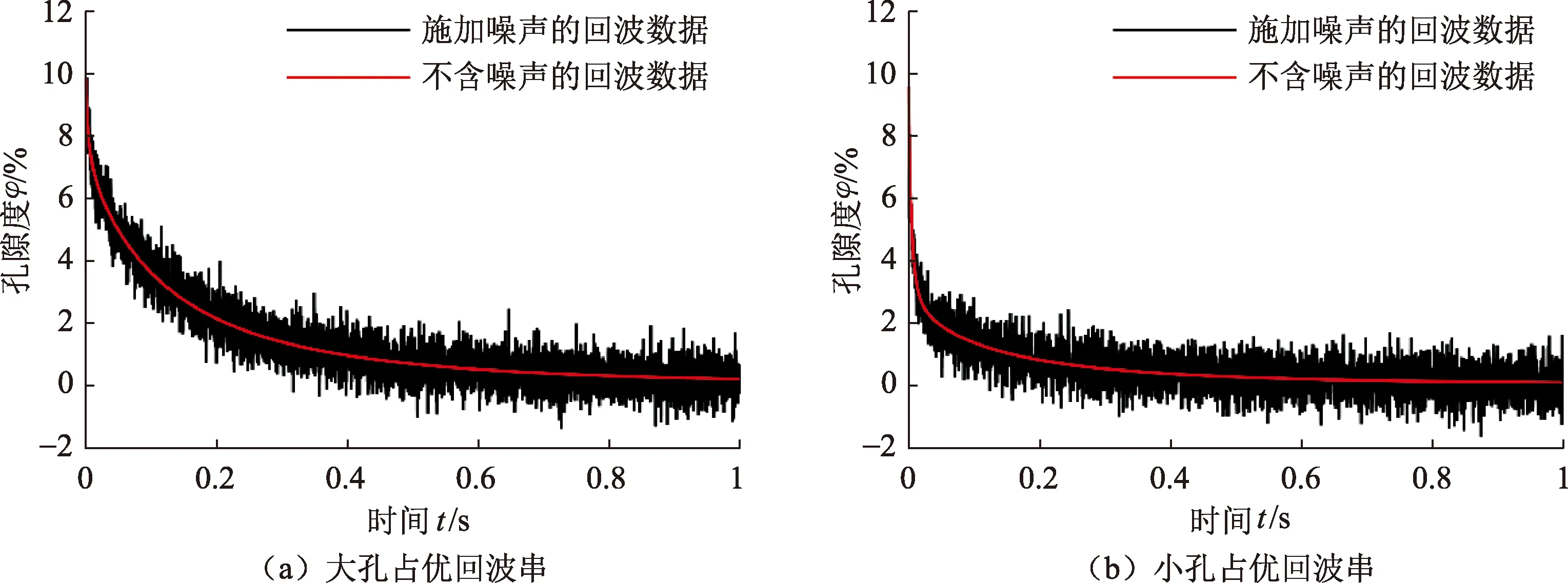
图5 大孔占优和小孔占优T2分布模型正演所得回波串Fig.5 Echo trains corresponding toT2distributions with more macropore and more micropore

为了提高NMR回波数据的反演速度,通常需要对回波数据进行压缩,本文中采用截断奇异值分解(truncated singular value decomposition)方法进行数据压缩[20]。经过压缩后,图5所示的每组回波均被压缩至20个回波。

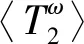
由图6(a)和图7(a)通过两种模型反演结果进行定性分析可知,ILT方法和ILT+方法在T2谱长弛豫部分反演结果基本相同,但在短弛豫部分,ILT+方法相比ILT方法反演结果精度更高,尤其是对于小孔占优模型,ILT+方法对反演结果精度的提高效果更明显。ILT+方法反演效果受所加先验信息种类及个数的影响,由图7(a)可知:ILT+S方法主要提高T2谱短弛豫部分幅值精度,对谱峰聚焦性提高较小;ILT+T方法提高了T2谱幅值精度和谱峰聚焦性,但对T2谱幅值精度的改善效果弱于ILT+T方法;ILT+ST方法则综合了ILT+S方法和ILT+T方法的优点,同时提高了T2谱短弛豫组分幅值精度和谱峰聚焦性,对幅值精度改善效果优于ILT+S,对谱峰聚焦性改善效果优于ILT+T。

图6(b)和图7(b)给出了反演结果与模型之间的绝对误差,其中黑色实线为ILT反演方法误差,绿色虚线为ILT+S反演方法误差,粉红色虚线为ILT+T反演方法误差,蓝色虚线为ILT+ST反演方法误差。可以看出,ILT方法和ILT+方法在T2谱长弛豫部分反演结果误差基本相同,但在短弛豫部分,ILT+方法相比ILT方法反演结果误差更小,反演精度更高,并且ILT+ST方法反演结果误差最小,ILT+S方法和ILT+T次之,ILT方法反演结果误差最大。

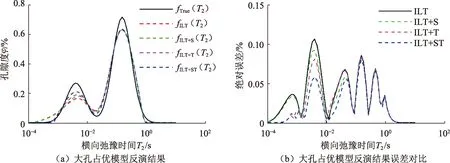
图6 大孔占优模型反演结果及误差对比Fig.6 Comparison of inversion results and errors of model with more macropore

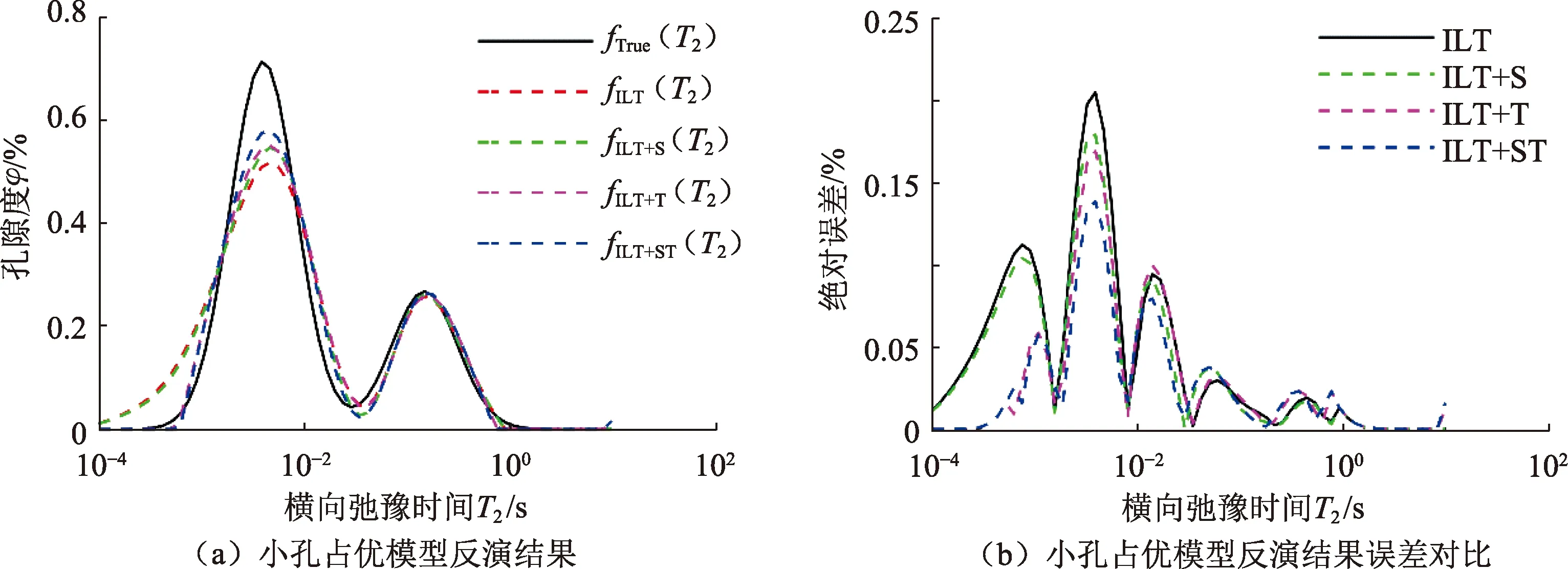
图7 小孔占优模型反演结果及误差对比Fig.7 Comparison of inversion results and error of model with more micropore

3 测井资料处理

数值模拟结果显示ILT+方法相比于ILT方法反演结果精度有所提高,尤其是对于T2谱短弛豫部分,效果更明显。非常规储层孔径较小,小孔部分占较大比重,ILT+方法对T2谱短弛豫部分反演精度的提高使得该方法在小孔占优的非常规储层中具有广阔的应用前景。

本文中选取一段致密砂岩储层NMR测井资料,其中NMR测井回波间隔为0.2 ms,回波个数为3 000,分别采用ILT、ILT+S、ILT+T和ILT+ST方法进行处理,处理结果如图8所示。其中,第1道为深度曲线(DEPTH);第2道为井径曲线(CAL)和自然伽马曲线(GR);第3道为原始NMR回波数据(ECHO);第4道为ILT方法反演结果;第5道为ILT+S方法反演结果;第6道为ILT+T方法反演结果;第7道为ILT+ST方法反演结果;第8道为各方法计算的孔隙度(实线为ILT+ST孔隙度,虚线为ILT孔隙度,黑点为岩心孔隙度)。由第4道和第5道反演结果对比可知,ILT+S方法主要提高了T2谱短弛豫部分的幅值精度;由第4道和第6道反演结果对比可知,ILT+T方法主要提高了短弛豫部分谱峰的聚焦性;由第4、5和第6道反演结果对比可知,ILT方法在T2谱短弛豫部分反演精度不高,不仅幅值偏低,而且谱峰聚焦性差,甚至反演不出短弛豫组分,ILT+ST方法则综合了ILT+S和ILT+T方法的优点,同时提高了T2谱短弛豫部分的幅值精度和谱峰聚焦性;第8道孔隙度对比则验证了ILT+ST方法的准确性,ILT方法由于对T2谱短弛豫部分反演精度不高,导致NMR孔隙度与岩心分析孔隙度相比普遍偏低,ILT+ST方法则由于对T2谱短弛豫部分反演精度的提高得到了更准确的孔隙度。实际井资料处理结果验证了ILT+方法的有效性和实用性。

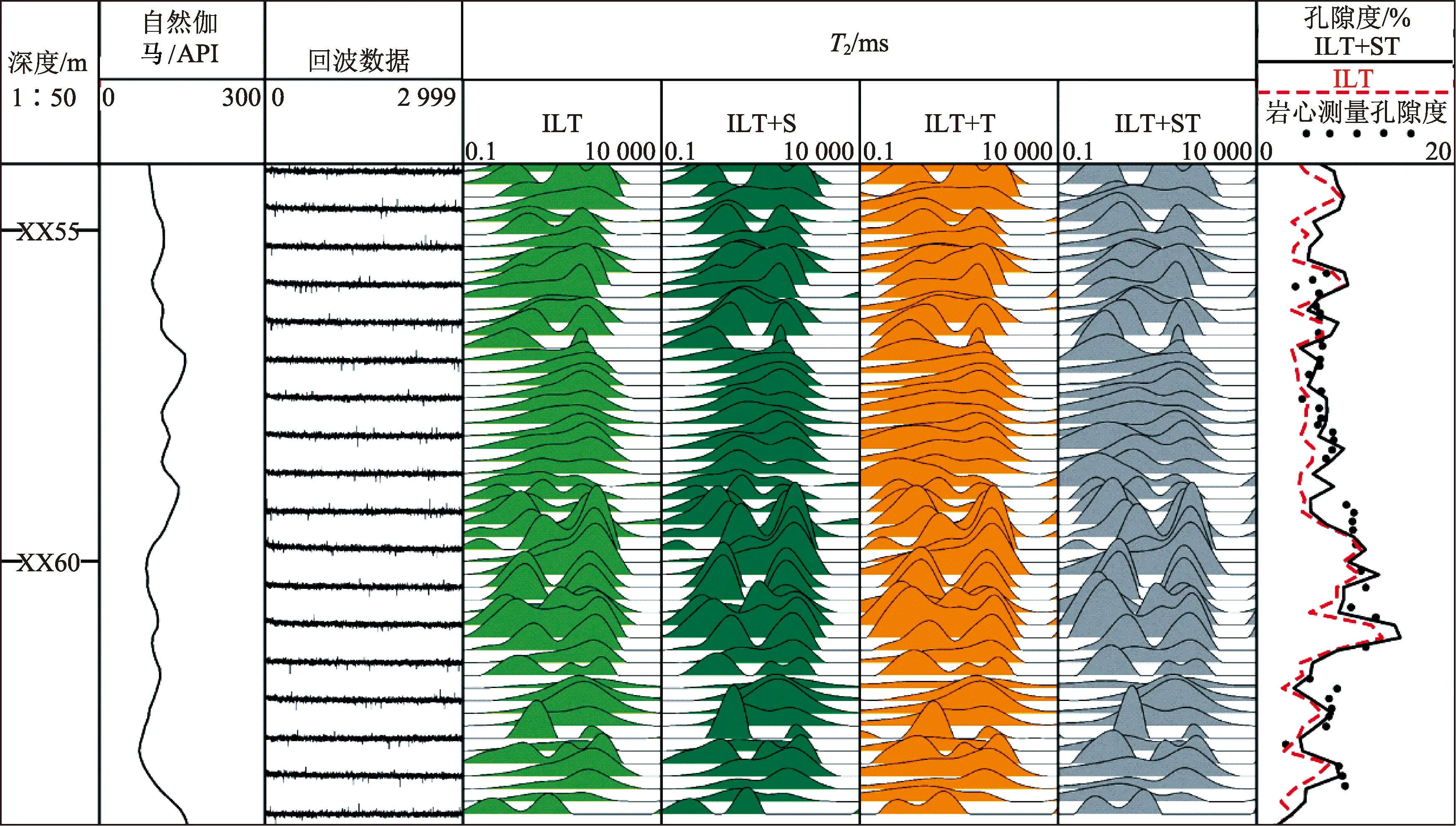
图8 ILT和ILT+方法反演结果对比Fig.8 Comparison of inversion results of ILT and ILT+

4 结 论

(1)针对NMR测井中T2谱短弛豫组分反演不精确的问题,提出基于先验信息约束的ILT+反演方法。该新方法提高了T2谱反演精度,不仅T2谱幅值更准确,而且谱峰更聚焦,尤其是对于T2谱短弛豫组分反演结果的改善效果更明显。

(2)施加不同先验信息作为约束条件对反演结果的改进效果不同。ILT+S方法主要提高T2谱短弛豫组分幅值精度,ILT+T方法主要提高T2谱短弛豫组分谱峰聚焦性,ILT+ST则综合了上述两种方法的优点,同时提高了T2谱短弛豫组分幅值精度和谱峰聚焦性。

(3)新方法对于小孔占优的致密砂岩、页岩等非常规储层的核磁共振回波数据反演具有广阔的应用前景。