基于免疫遗传算法的堆石坝流变反演分析

(上海勘测设计研究院有限公司，上海 200434)

流变是高土石坝变形中的一个重要因素，在设计时正确合理地计入流变变形的影响，并通过施工措施降低堆石体的变形量，是保证大坝安全运行的关键。因此在高土石坝设计与施工中，运用数值分析方法计算预测坝体的变形及其趋势，进行堆石坝的设计优化，是高土石坝持续发展的重要因素[1]。

利用原位监测资料，通过计算和反馈分析土石坝实际工作状况[2]，对已建成大坝可更好地评价其安全状况；对在建的大坝，通过原型监测资料进行反分析，对优化堆石坝设计以及改进施工也有重大意义[3]。在土石坝应力变形计算中，参数的选取准确与否关系到数值计算结果是否能符合土石坝的实际情况。反演分析应用现场监测资料反算土石坝参数，能较精确地确定土石坝参数，把数值分析和监测技术有机地结合在一起[4]。近年来，引入了人工神经网络等智能算法，进一步优化了参数的反分析效率。2005年，张丙印、袁会娜运用人工神经网络和演化算法进行位移反分析[5]。2006年，朱晟、张美英将基于免疫学原理的遗传算法应用于堆石坝材料力学参数的位移反分析中，该方法克服了标准遗传算法收敛方向无序性且容易局部早熟的缺点，在反分析中取得了很好的应用效果[6-7]。

在瀑布沟心墙堆石坝材料室内三轴试验成果基础上，本文通过瀑布沟心墙堆石坝的原型监测资料，基于免疫遗传算法对其流变参数进行反演，并对反演所得参数的合理性进行了验证分析。

1 计算模型及免疫遗传反演算法

1.1 增量流变本构模型

国内对堆石流变的研究，最早始于由沈珠江根据堆石流变试验提出的三参数流变模型[8]，该模型在土石坝的流变分析中得到了广泛的应用。三参数流变模型以应力全量形式推导，未考虑应力加载路径。当土石坝有限元分析计算采用增量荷载时，无法考虑该级增量荷载之前流变的影响，堆石体流变的遗传特性难以体现。因而，本文采用由朱晟在此基础上提出的可反映应力路径影响的7 参数增量流变模型[9]，该模型已应用于水布垭土石坝计算分析中[10]。

结合堆石料三轴流变试验资料，增量流变模型从中得到流变体积模量和剪切模量等模型参数，模型参数分别为ks，ns，kv，Rsf，c，α，其数值可根据三轴流变试验成果或大坝原型监测资料反演确定。

(1)

(2)

式中，σvi，σsi分别为体积应力和广义剪应力；Ki，Gi为控制滞后变形部分的参数，称为流变体积模量和流变剪切模量，是相应加载应力路径下应力状态的函数；c，α为试验常数。

不同应力状态下，体积应力和最终体积流变近似为线性关系，可以认为流变体积模量一般随试验围压的变化而变化，以式(3)近似表示：

(3)

式中，Pa为大气压力，kv，nv为模型参数，可根据试验结果整理得到。

不同应力状态下广义剪应力和最终剪切流变近似为双曲线关系，流变剪切模量为

(4)

式中，S为应力水平，Rsf为破坏比，ks，ns为模型参数，可根据试验资料整理得到。

1.2 目标函数及反演参数

堆石料占大坝体积的绝大部分，是影响坝体沉降的最主要因素，同时参考监测仪器的布置位置，在反分析时主要反演大坝心墙、下游主堆石区和次堆石区的坝料参数[11]。

通过监测点的实测位移量与计算位移值的差异，构造目标函数，形成IGA 抗原。在监测仪器埋设初期时段，各种因素的干扰较大，目标函数需要采用增量时段计算；同时，为了考虑不同测点测值权重和消除不同物理量的量纲，建立目标函数[12-13]如下：

(5)

增量流变模型待反演流变参数为X={ks，ns，kv，nv，Rsf，c，α}。

1.3 基于IGA的流变参数反演算法

1.3.1抗体编码

采用浮点数编码方式，模型共7个参数，因此就有7个基因。假设初设种群数为N，随机产生7×N个小于1的实数，αi1,αi2,…,αi7(i=1,2,…,N)取初始种群第i个抗体的7个基因分别为

(6)

式中，aji,bji为第i个抗体中第j个基因的取值范围，可参考类似工程分析取值。重复N次，就可以取得初始抗体群X1,X2,…,XN。

1.3.2构造适应度函数

首先将获得的初始抗体群按目标函数计算值进行升序排列，采用Michalewicz提出的非线性排序的选择概率计算公式建立适应度函数：

f(Xi)=α(1-α)i-1

(7)

式中，i为个体排序序号，α∈(0,1)。

从式(7)可以看出，个体被选中的概率与个体的排序位置有关，排序位置越前适应度越大，因此排序前的个体被选中概率大，合理的适应度函数可避免算法局部收敛或搜索停滞。

1.3.3记忆细胞库更新

将每代种群中的所有个体根据适应度值的大小进行降序排列，选取前M个个体存入记忆细胞库，完成记忆细胞库得换代更新过程。

1.3.4基于浓度的适应度调整

为保证个体的多样性，提高算法的全局搜索能力，根据抗体间欧氏距离和适应度来计算抗体间的相似度和抗体浓度。记抗体Xi和Xj的欧氏距离为D(Xi,Xj)，适应度分别为f(Xi)和f(Xj)，取适当常数η>0，t>0，如果两个抗体满足式(8)：

(8)

则认为抗体Xi和Xj相似，抗体Xi的浓度即为与抗体XJ相似的抗体个数除以抗体总数，记为Ci。则抗体Xi适应度函数根据浓度修正为

(9)

式中，α，β∈(0,1)，fmax(Xi)为所有抗体的最大适应度值，Ci为抗体Xi的浓度。

从式(9)可以得出：对于抗体Xi，采用上述浓度调节后，浓度对选择几率影响减小，若抗体浓度高且适应度较高，获得的适应度补偿就较少，可避免使计算陷入局部极优；而抗体浓度不高但适应度高，得到适应度补偿就会相对较高，增加了该抗体的选择概率。

1.3.5选择操作

个体的选取概率P由根据浓度修正过的适应度函数值计算得来：

(10)

图1 土石坝流变参数反演分析流程Fig.1 Program of back analysis for earth-rock dam rheological parameters

基于选取概率，用轮盘赌选择方式来产生新的个体，适应度值较高的个体容易被选择，同时由于是采用相对值进行判断，避免过大适应度值的绝对性影响，避免过早收敛。

1.3.6交叉与变异

交叉运算选择算术交叉算子，由两个个体的线性组合而产生两个新的个体，交叉概率取0.8。变异采用的是均匀变异算子，确定作为变异点的各个基因座的位置后，通过变异概率对各个变异点进行随机变异，变异概率取0.1。

1.3.7群体更新

将最终获得的个体和记忆细胞库中本身的M个体合并在一起，得到一个新种群，然后再根据适应度值进行降序排列，将前M个个体更新进入记忆细胞库中，下一代群体则为剩余N个个体。

1.3.8终止条件

当目标函数值低于某个值或进化代数超过预先设定值，则反演计算终止，此时得到参数即为所需值。

结合免疫遗传算法和堆石坝流变有限元分析过程，流变参数反演过程如图1所示。

每个坝体分区堆石料的力学特性参数包括瞬变参数(邓肯张E-v模型参数：Rf，K，n，G，F，D)和流变参数(ks，n，kv，nv，Rsf，c，α)。在填筑期，占坝体大部分体积的堆石料的瞬时变形占主导，影响位移计算值的主要因素是E-v模型参数，因此在反演获得流变参数后还需要对室内三轴试验的E-v模型参数进行反演修正。

2 实际工程应用

2.1 瀑布沟堆石坝概况

瀑布沟水电站位于大渡河中游、四川省汉源县和甘洛县境内，最大坝高186 m，总库容53.90亿m3。水库正常蓄水位850.00 m，死水位790.00 m。在坝体中布置的各种监测仪器中，坝体位移的原型监测数据相对准确，取得的资料也较多，可以作为反演分析的基础。瀑布沟心墙堆石坝在0+240共布设3组电磁式沉降仪VE1～VE3，其具体分布见图2。

2.2 流变参数反演分析过程

在对堆石料流变参数进行反演之前，需要首先确定大坝各个分区的瞬变参数。根据室内三轴试验提供的资料，瀑布沟心墙坝各个分区的参数见表1，并在此基础上进行流变参数的反演。

大坝现场实际测量的变形观测值包括瞬间变形分量和流变变形分量。为了尽量排除自重等外荷载所引起的瞬时变形分量的干扰，从堆石体的总变形中获得合理的流变变形，选择1～3个月大坝停工阶段或者大坝竣工后外荷载基本不变的时期，此时堆石的变形主要为流变变形，反演分析得出的流变参数较为合理。

根据施工情况，瀑布沟心墙堆石坝不存在完全停工阶段，但对某些测点来说，在某些时段坝体的填筑方量较小且对监测点影响较小，瞬间变形影响较小，适于进行流变分析。因此，可以认为此时段内监测点相对位移为该时段内对应节点的流变量。根据瀑布沟施工过程，共选取3段时间进行分析：① 2008年7月21日至2008年9月5日，该时段内大坝心墙及下游主次堆石区维持至769 m高程不变，只有上游堆石区局部由769 m填筑至775 m高程，如图3所示。② 2008年10月21日至2008年12月15日，该时段大坝心墙及下游主次堆石区填筑至795 m高程，只有上游堆石区780 m至786 m高程局部进行堆石体填筑，如图4所示。③ 2009年4月25日至2009年6月23日，大坝进行坝体下游压重部分施工，如图5所示。可基本认为这3段参考水布垭面板堆石坝施工与运行性状反演研究[10]，流变参数初始取值范围见表2。

图2 瀑布沟0+240断面电磁式沉降仪布置Fig.2 The electromagnetic settling instrument at 0+240 section of Pubugou Core Rockfill Dam

图3 截止至2008.9.5 大坝断面(0+240)Fig.3 The dam section up to 2008.9.5(0+240)

时间内大坝各监测点的沉降值主要是流变变形，可以利用这段时间内测得的资料进行流变参数的反演分析[14-16]。

表1 瀑布沟心墙坝坝料E-v模型参数Tab.1 E-v mode parameters of Pubugou core rockfill dam

目标函数的进化过程如图6所示，到29代时，目标函数基本稳定，到35代时，停止计算，得到反演参数。心墙及主次堆石反演所得流变参数见表3。

2.3 E-v模型参数反演修正

分析时间为2008年1月31日至12月31日，大坝从738.0 m高程填筑到799.0 m高程。参考室内试验参数，拟定心墙堆石、主堆石和次堆石区邓肯张E-v模型参数的搜索区间如表4所示，最后得到的反演修正参数如表5所示。

3 反演成果分析验证

为验证所获得的参数的合理性，选取典型监测结点，分析其沉降、水平位移、应力随时间变化的过程，并与实测值进行比较。0+240断面典型监测点位置如图7所示。

表2 流变模型参数的初始取值范围Table.2 The variation range of rheological parameters

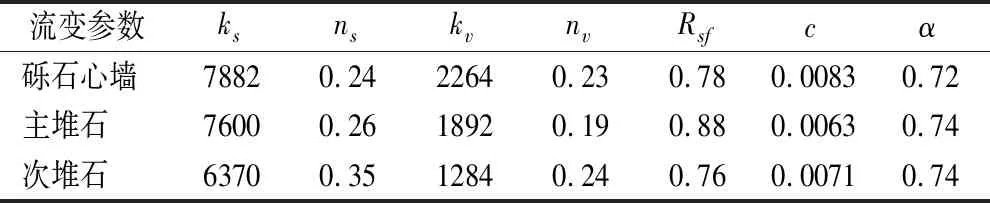
表3 反演所得的流变参数Table.3 The rheological parameters obtained from the inversion

3.1 堆石测点时程曲线对比分析

3.1.1沉 降

图8为典型测点的沉降时程曲线对比图。由图中可见：典型测点的计算沉降与实测沉降数值上相差不大，随时间的变化规律也基本相同。但在填筑初期，计算沉降与实测沉降较为吻合，填筑后期，计算沉降略大于实测沉降。主要原因为仅以2008年7月21日至9月5日实测沉降反演得到的参数仅能较好地反映此时间段以前的土石坝堆石流变及瞬变参数，对于之后的填筑过程模拟会存在一定的误差。总体而言，各典型测点的计算沉降与实测沉降吻合度较好，说明由反演所得的土石坝瞬变参数和增量流变参数较为合理，能满足对土石坝进行数值分析的要求。

图4 截至2008.12.15 大坝断面(0+240)Fig.4 The dam section up to 2008.12.15(0+240)

图5 截至2009.06.23 大坝断面(0+240)Fig.5 The dam section up to 2009.6.23(0+240)

图7 0+240断面典型测点位置示意Fig.7 Position diagram of typical monitoring point at 0+240 section

图6 目标函数随进化代数变化图Fig.6 Change process of target function

表4 E-v模型参数的初始取值范围Table.4 The variation range of E-v mode parameters

3.1.2水平位移

图9为典型测点水平位移时程曲线对比图。各典型测点的计算与实测位移在数值上相差不大，变化规律类似，但存在部分数值在填筑初期吻合度较差。这是因为在水平位移较小情况下，监测仪器存在一定的初始误差。

3.1.3应 力

从图10中可以看出，土石坝堆石的计算正应力变化规律与实测正应力变化规律一致，并且数值上也相差不大，说明了反演所得参数较为合理。

3.2 防渗墙测点时程曲线对比分析

与堆石位移监测值相比较，防渗墙位移测值较为精确。由图11可以看出，由反演所得参数计算得到的防渗墙水平位移与实测水平位移较为接近，且变化规律一致，较为准确地模拟了防渗墙的变形情况，说明了反演所得土石坝参数的合理性。

3.3 坝体变形应力分析

大坝有限元计算分析采用邓肯张E-v模型和增量流变模型，参数均采用上述分析成果。

3.3.1坝体变形

图12～13为0+240号断面竣工期坝体上下游方向水平位移和竖向位移等值线分布图。竣工期，0+240断面上下游方向位移均指向坝坡方向，向上游的最大水平位移为42.6 cm，位于上游高程730 m处；而向下游移动的最大水平位移为42.0 cm，位于下游高程720 m处。坝体的最大沉降为195.4 cm，位于高程740 m处的心墙部位。

表5 反演所得的E-v模型参数Table.5 The E-v mode parameters obtained from inversion

3.3.2坝体应力

图14～15分别为0+240断面竣工期坝体主应力等值线分布图。此时坝体主应力基本与坝坡平行，并从坝顶部向坝基处呈现加大的趋势。坝体第一主应力极值为3.60 MPa，第三主应力极值为1.30 MPa。

竣工期坝体最大沉降为195.4 cm，约占坝高的1.1%，向下游水平位移增大至42.6 cm，向上游最大位移为42.0 cm，基本符合瀑布沟心墙坝的变形应力特性，与实测资料吻合良好。

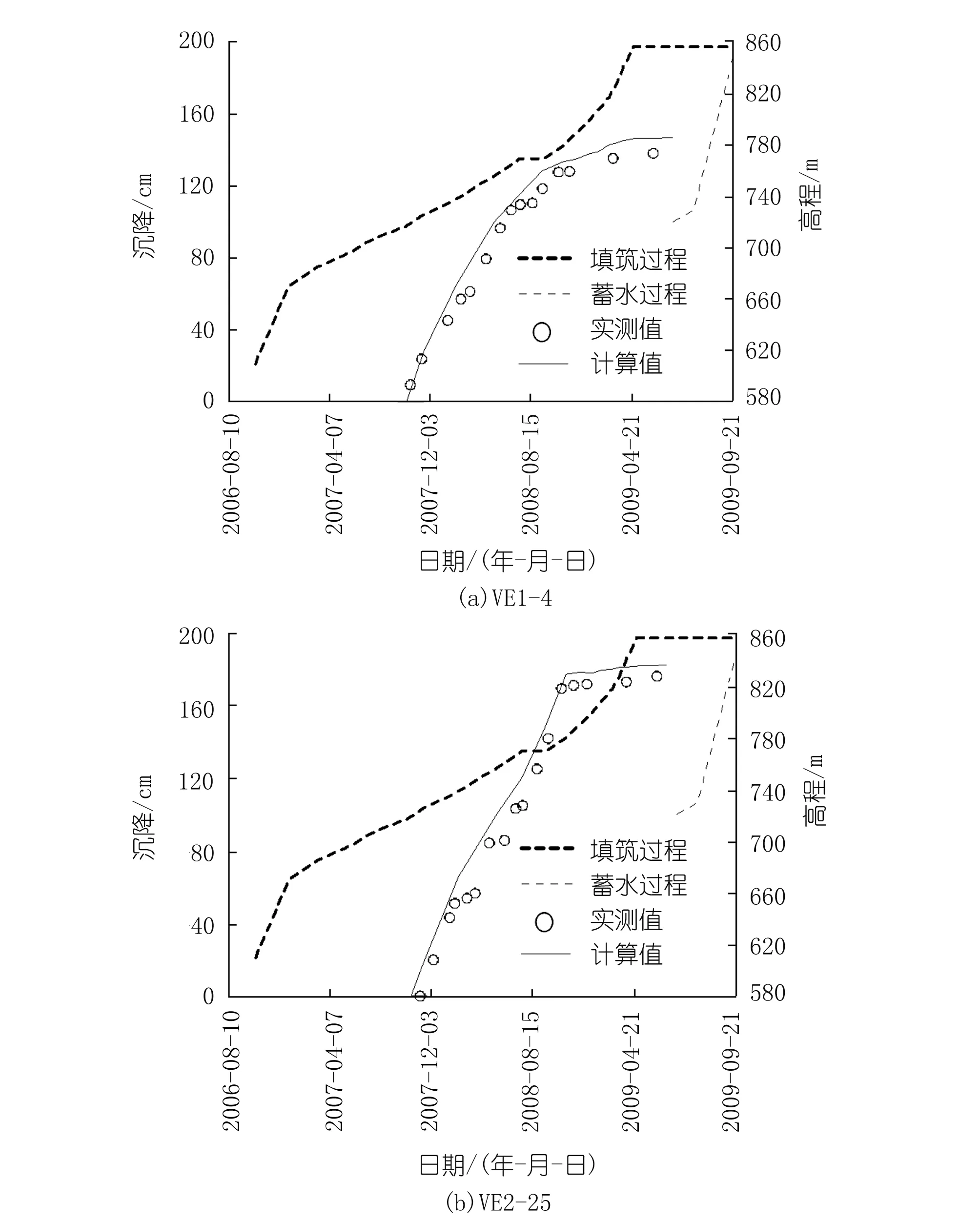
图8 堆石典型监测点的沉降时程Fig.8 Settling procedure of typical monitoring points of rockfill

图10 典型监测点的土压力时程Fig.10 Soil pressure at typical monitoring points of rockfill

图9 堆石典型监测点的水平位移时程Fig.9 Horizontal displacement at typical monitoring points of rockfill

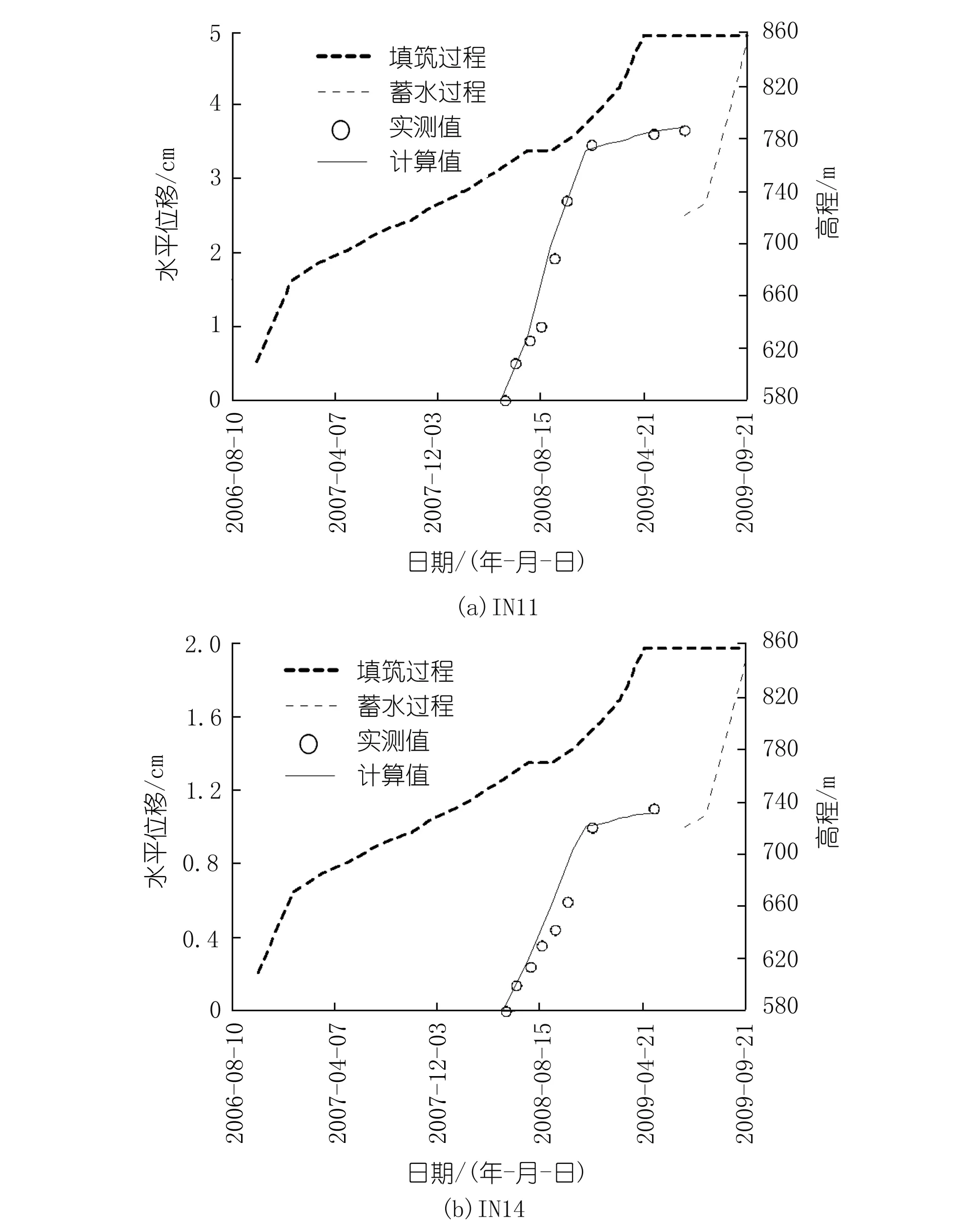
图11 防渗墙典型监测点的水平位移Fig.11 Horizontal displacement at typical monitoring points of cut-off wall

图12 竣工期0+240断面水平向位移(单位：cm)Fig.12 Horizontal displacement of 0+240 section at completion period (unit: cm)

图13 竣工期0+240断面竖直向位移(单位：cm)Fig.13 Vertical displacement of 0+240 section at completion period (unit: cm)

图14 竣工期0+240断面第一主应力(单位：MPa)Fig.14 The major principal stress of 0+240 section at completion period (unit: MPa)

图15 竣工期0+240断面第三主应力(单位：MPa)Fig.15 The minor principal stress of 0+240 section at completion period (unit: MPa)

4 结 论

(1) 对典型测点的位移应力及坝体变形应力分析表明，运用免疫遗传算法对瀑布沟心墙堆石坝反演的流变参数较为真实地反映了土石坝堆石料的流变特性。

(2) 在免疫遗传反分析过程中，每一次求解过程都需反复调用正分析程序，以优化初始参数搜索空间，减少目标函数稳定进化代数，这对减少计算时间，提高反演效率有着重要意义。