大跨径斜拉桥主梁线形测控新方法研究及应用
顾玄龙,刘成龙,李 雷,沈卢明,蒋 涛,杨雪峰
(1. 西南交通大学地球科学与环境工程学院,四川 成都 611756; 2. 西南交通大学高速铁路运营安全空间信息技术国家地方联合工程实验室,四川 成都 611756; 3. 中铁第四勘察设计院集团有限公司,湖北 武汉 430063; 4. 四川公路桥梁建设集团有限公司,四川 成都 610041)
宜宾南溪长江公路大桥是国家规划的长江干线新建过江通道重点项目,项目起于长江北岸江北片区新城干道第一个平交路口,跨越长江后连接引道与江南片区规划干道,桥位路线总长2100 m,桥长1 503.82 m。桥梁孔跨布置为9×30 m(小箱梁)+3×60 m(连续梁)+(280 m+572 m+189 m),主跨为双塔双索面斜拉桥。北岸边跨及主跨主梁采用钢—混凝土叠合梁,南岸边跨主梁采用双纵肋混凝土主梁,是世界上首例采用两侧边跨不对称设计的大跨径叠合梁斜拉桥。
该桥主梁结构刚度小、跨度大,变形大,因此主梁在安装施工时,必须精确测量各种工况下主梁平面位置和竖向线形,以保证合龙过程顺利。传统的斜拉桥主梁施工期间平面位置的定位是采用固定测站的极坐标法[1-2],但这种方法易受现场复杂的施工环境干扰,且测量网形单一,检核条件少。因此,本文提出利用大桥平面控制网中的控制点,采用全站仪自由设站法[3]测量主梁测点的平面坐标。同时区别于传统的水准测量方法,提出采用全站仪中间法三角高程[4]进行间接高差的测量,得到主梁竖向线形,并通过实例证明采用间接高差测量法可以达到二等水准测量的精度。经过施工验证,本文所用的测控方案较传统的极坐标法和水准测量更加合理、简便、快速,并且在满足测量精度的前提下测量效率显著提高。
1 大跨径斜拉桥主梁线形测控新方法测量原理
该桥北岸边跨和中跨斜拉桥主梁为钢主梁与混凝土桥面板共同受力的叠合梁,南岸边跨及南岸索塔根部为混凝土主梁。主梁北岸13#塔岸侧共19个节段加边跨合龙段、现浇段,13#塔江侧21个节段;南岸14#塔江侧20个节段,两者中间是中跨合龙段,14#塔岸侧为混凝土梁段。每个钢主梁标准节段长13.5 m,每个节段施工工况分别为:吊机悬臂钢主梁拼装→斜拉索初张→预制桥面板安装→湿接缝现浇→斜拉索单向张拉→斜拉索整体张拉。
每个标准节段主梁线形测控的内容包括:①悬臂端梁段拼装完成后,测量本节段及相邻的已施工4个节段共4个平面测点、14个高程测点,测点具体位置见下文;②斜拉索初张后,测量本节段及上一节段前端上、下游侧共4个高程测点;③桥面板湿接缝浇筑后,测量内容同斜拉索初张后;④斜拉索二张后,测量内容同梁段拼装完成后。根据文献[5]规定,悬臂拼装主梁轴线偏位不大于10 mm,主梁竖向偏差不大于6 mm。主梁的施工测控需保证节段的平面和竖向线形满足设计要求,直至边跨、中跨的合龙,精度要求高,因此需要精确定位各个节段主梁的平面和竖向线形。
1.1 基于自由设站法的主梁平面位置测量原理
传统的主梁平面位置定位是在索塔主梁0#块顶面设置加密控制网点并用固定测站采用极坐标法进行测量。由于施工现场环境复杂,主梁桥面密布施工机具和桥面吊机,观测视线极易被遮挡,因此采用固定测站极坐标法的测量效率低,而且随着主梁长度的增长定位精度也随之降低。因此在大型斜拉桥主梁施工平面线形测控过程中,笔者提出利用大桥控制网中的3个及以上控制点,采用全站仪自由设站法测定主梁上测点的平面坐标。
全站仪自由设站法定位测点平面坐标的原理如图1所示,全站仪从任意测站点观测已知控制点(一般不少于3个)的方向和距离,并按照间接平差法通过已知坐标和边角观测值求得测站点坐标及其定向角未知数,并据此测量待测点的坐标[6]。自由设站测量间接平差是以待定点的坐标及其定向角平差值作为未知参数,先按边角后方交会计算出测站点坐标和定向角未知数的近似值,据此计算测站点到各已知点的近似坐标方位角和边长,再根据方向观测值和边长观测值建立方向和边长误差方程式,最后按最小二乘原理计算测站点坐标和定向角未知数平差值[7]。限于篇幅本文仅给出未知数平差值及其精度评定公式。未知数平差值计算式为[8]
dX=(BTPV)-1BTPL
(1)
同时求得验后单位权中误差为
(2)
式中,r为自由度;n为观测值个数;t为必要观测数。
由此可求得自由设站点平面坐标及定向角平差值
(3)
并按照协因数传播律,得到自由设站站点坐标及定向角协因数阵为
(4)
进一步可算出自由设站点X、Y坐标及定向角未知数ω中误差为
(5)
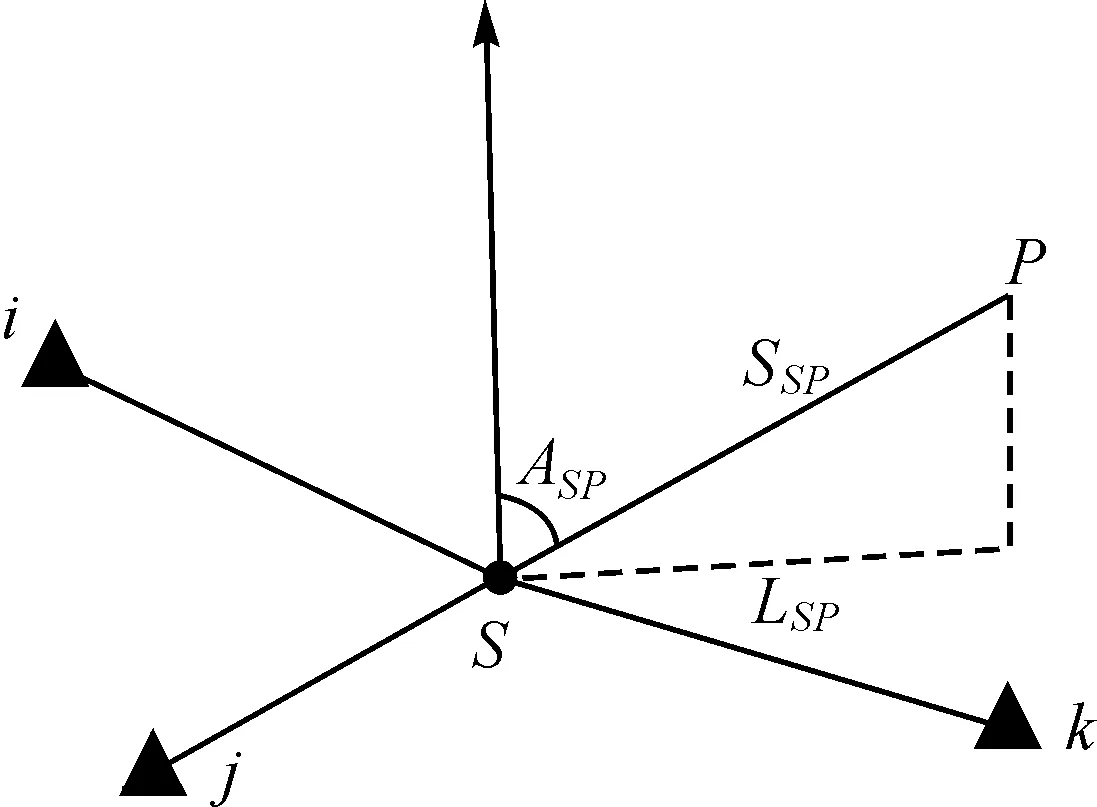
图1 全站仪自由设站测量平面坐标原理
自由设站测量完成后,得到设站点平面坐标及定向角平差值XS、YS、ω,之后全站仪观测前视点得到水平方向LSP、天顶距ASP、斜距SAP,则前视点的坐标计算式[7]为
(6)
1.2 基于间接高差传递方法的主梁竖向线形测量原理
传统的主梁竖向线形测量是采用电子水准仪进行二等水准测量,但由于现场施工的需求,在悬臂端钢主梁拼装完成后及一张、二张索力张拉时,都需要快速准确地获取主梁竖向线形,并且随着主梁节段数量和悬臂长度的增加,水准线路越来越长,加上桥面施工机具多和场地小,因此传统水准测量方法在大跨径主梁竖向线形测量过程中效率低[9]。为此,本文提出利用高精度智能型全站仪(1 mm+1×10-6D,0.5″),采用中间法三角高程间接高差的测量方法测定主梁的竖向线形。该方法首先通过全站仪间接高差测量的方法,将地面高程控制网的水准点高程传递到主梁0#块附近的索塔柱侧壁上,作为主梁竖向线形测量的起算点(又称工作基点),之后再通过该方法得到主梁上各个测点的高程。
下文以该桥北岸索塔0#块上工作基点高差传递为例,简述中间法三角高程间接高差测量的原理[10-11]。如图2所示,北岸索塔底部A点高程已知为HA,B点高程待求为HB,将全站仪架在岸上合适的位置(自由测站),分别对B、A点进行观测,斜距为S1、S2和竖直角为V1、V2(V2为负角)。
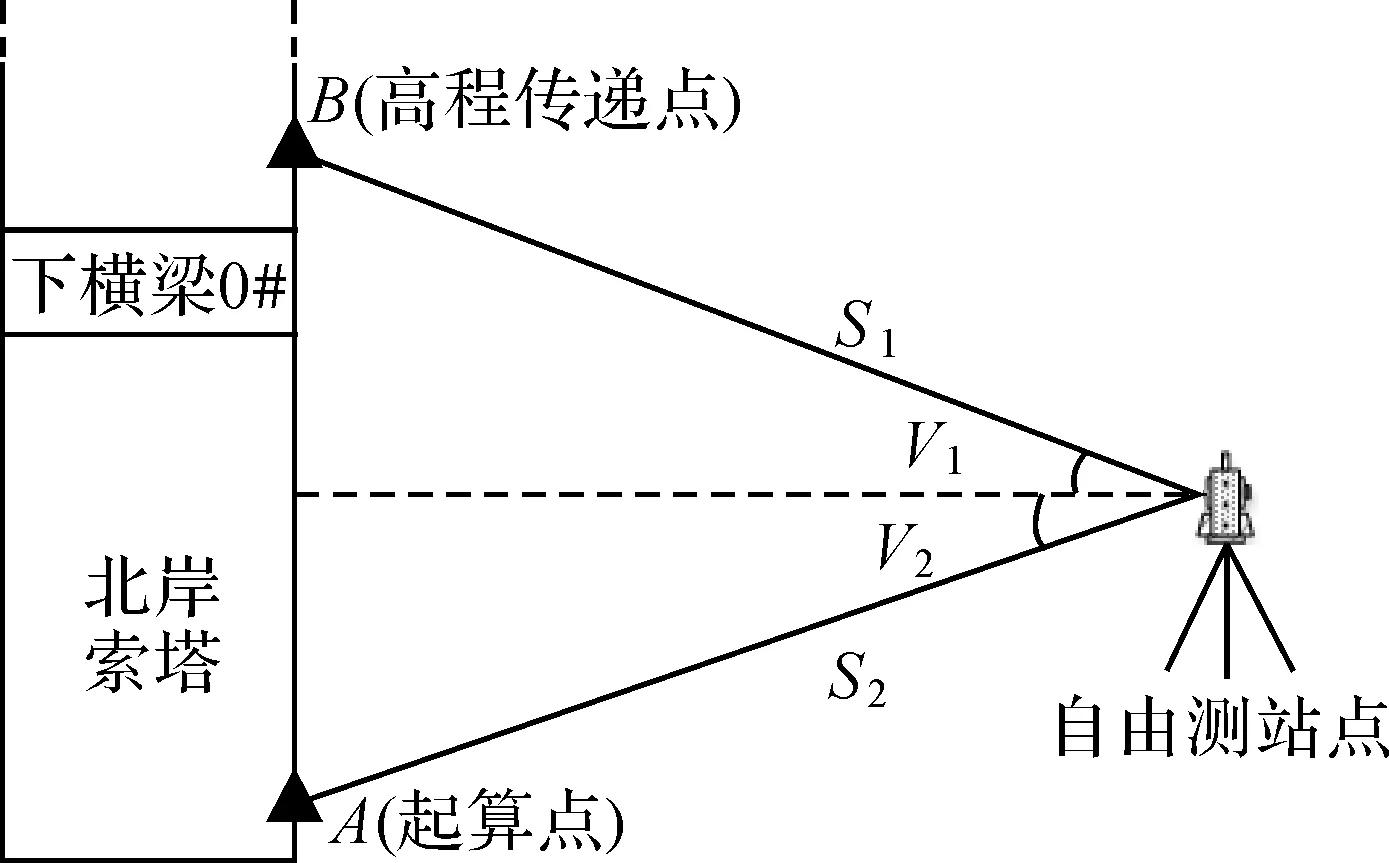
图2 中间法三角高程间接高差测量原理
采用中间法三角高程间接高差测量时,A、B两点采用如图3所示的西南交通大学发明的高速铁路CPⅢ测量标志组件,其棱镜中心和高程杆圆球同心,圆球直径为2 cm,该标志组件的特点是在其上既可进行水准测量又可进行全站仪测量。由于在A、B点上棱镜中心就是测点所在位置,因此A、B两点的棱镜高均为0,在岸侧的自由测站点观测A、B两点,仪器中心就是测站点,因此无需量测仪器高,采用这种方法进行高程传递时避免了量取棱镜高和仪器高时带来的误差。
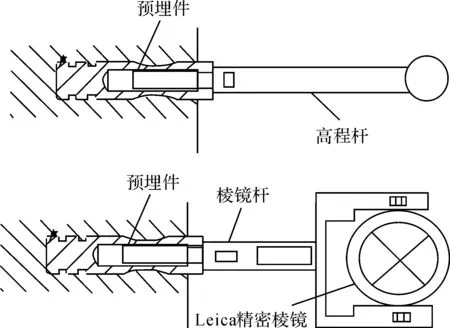
图3 西南交通大学高速铁路CPⅢ测量标志组件
AB间的间接高差hAB计算公式为
hAB=S1sinV1-S2sinV2+f1-f2
(7)
式中,f1、f2分别为观测B、A点时的地球曲率和大气折光对间接高差的影响值,其计算方法如下
(8)
式中,K1、K2分别为B、A方向的垂直大气折光系数;R为地球的曲率半径。
若令D1=S1cosV1,D2=S2cosV2,则式(7)可写成
(9)
采用中间法三角高程测量过程中选择自由测站时尽量使:D1≈D2=D,而测量B、A时又是在同一环境条件下观测的,则有K1≈K2≈K,综上则有f1≈f2=f,因此A、B两点间的间接高差为
hAB=S1sinV1-S2sinV2
(10)
此时B点的高程计算公式为
hB=hA+hAB
(11)
由式(10)可知,采用中间法三角高程测量在计算两点之间的间接高差时可有效减弱球气差对A、B两点之间高差的影响,且不用测量仪器和棱镜高。
2 新方法应用实例
下文以该桥北岸索塔边跨钢主梁悬臂端拼装完成后主梁线形测控为例,详述采用全站仪自由设站测控主梁平面线形,以及采用全站仪间接高差进行主梁竖向线形测控的方法。该大桥每节段主梁在施工时,需要对此节段(BN8)及相邻的4个节段(BN4、BN5、BN6和BN7)进行线形测控。如图4所示,主梁平面线形测控需准确定位BN8、BN7节段上的测点T1、T2平面坐标,共需测量2个节段共4个测点平面坐标;主梁的竖向线形测控需准确定位BN8、BN7节段上的测点T1、T2、T3、T4,以及BN4、BN5和BN6节段上的测点T1、T2的高程,共需测量5个节段上14个高程测点。之所以竖向线形测控需要测控5个节段上的14个高程测点,是因为主梁上每一个节段的施工,均对待安装的节段和已安装的节段的高程影响显著,因此竖向线形测控是大跨度斜拉桥施工监控的主要内容之一。
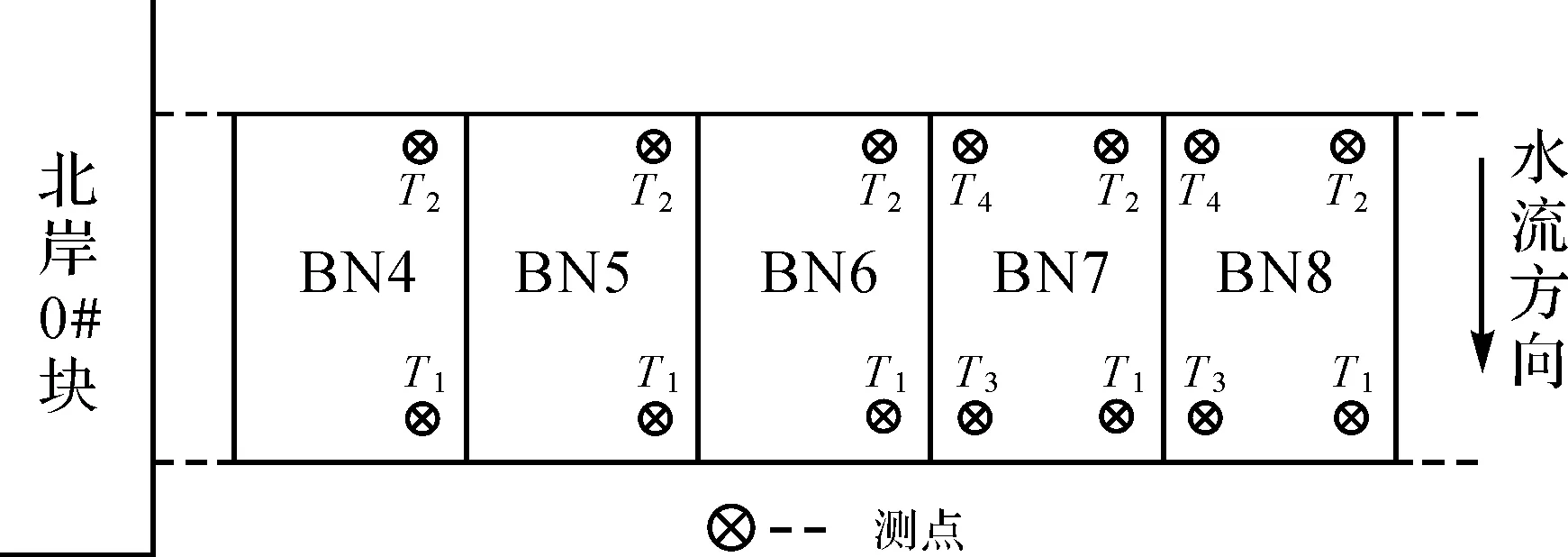
图4 北岸边跨主梁上各个节段测点布置
2.1 基于自由设站法的主梁平面线形测量方法及精度分析
根据文献[5]主梁施工监控测量规定,测量过程应尽量选择无风或微风的天气,以排除风荷载的影响,在主梁上进行测量时应停止机械施工,且在夜间(0:00~7:00)温度恒定短时间段内完成测量工作。如图5所示,在该桥主梁平面线形测控时,笔者提出采用全站仪自由设站法进行测点平面坐标测量,其测量原理和主要步骤分别为:
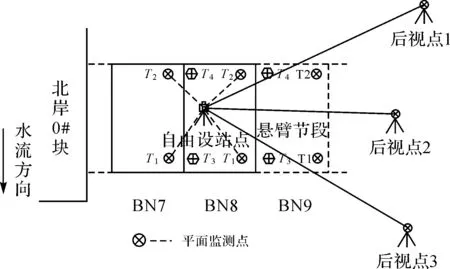
图5 自由设站法主梁平面线形测量
(1) 将全站仪架设在主梁BN7、BN8节段T1、T2共4个平面测点构成的网形大致中间的位置,精平并设置大气参数,后视3个平面坐标已知的地面控制点进行自由设站测量。
(2) 自由设站测量完成后,得到站心平面坐标、定向角及设站精度并记录,要求X、Y方向坐标中误差<5 mm。
(3) 在对主梁平面测点测量之前及测量完成后,都需要测量已知控制点的坐标,并与其已知坐标进行比较,作为设站检核,要求控制点实测X、Y坐标与已知值较差<±5 mm。
(4) 设站精度及坐标检核满足要求后,全站仪半盘位测量主梁BN7及BN8节段上测点T1、T2坐标并记录。
(5) 如图5所示,全站仪大致位于BN7及BN8节段测点构成的网形中心,且测点采用定长徕卡精密棱镜对中装置,为节约测量时间,在测量测点坐标的同时记录BN7及BN8节段上6个测点的高程值,则可进一步得到图5中6个测点间的相对高差。
(6) 为保证主梁平面坐标测量结果的准确性,将全站仪在小范围再次设站测量,重复上述5个步骤,重复设站测量,进行测点平面坐标的站间检核,若两次测量的测点X、Y坐标较差<±3 mm则满足精度要求,取两次测量的坐标均值为主梁施工测控的依据。
该桥北岸索塔边跨叠合梁安装施工已进行了8个节段(含0#块),中跨进行了7个节段,叠合梁施工监控测量在悬臂端梁段拼装完成及索力二张后共进行了36次自由设站测量,每次自由设站测量后的X、Y坐标及其点位中误差统计情况如图6所示。
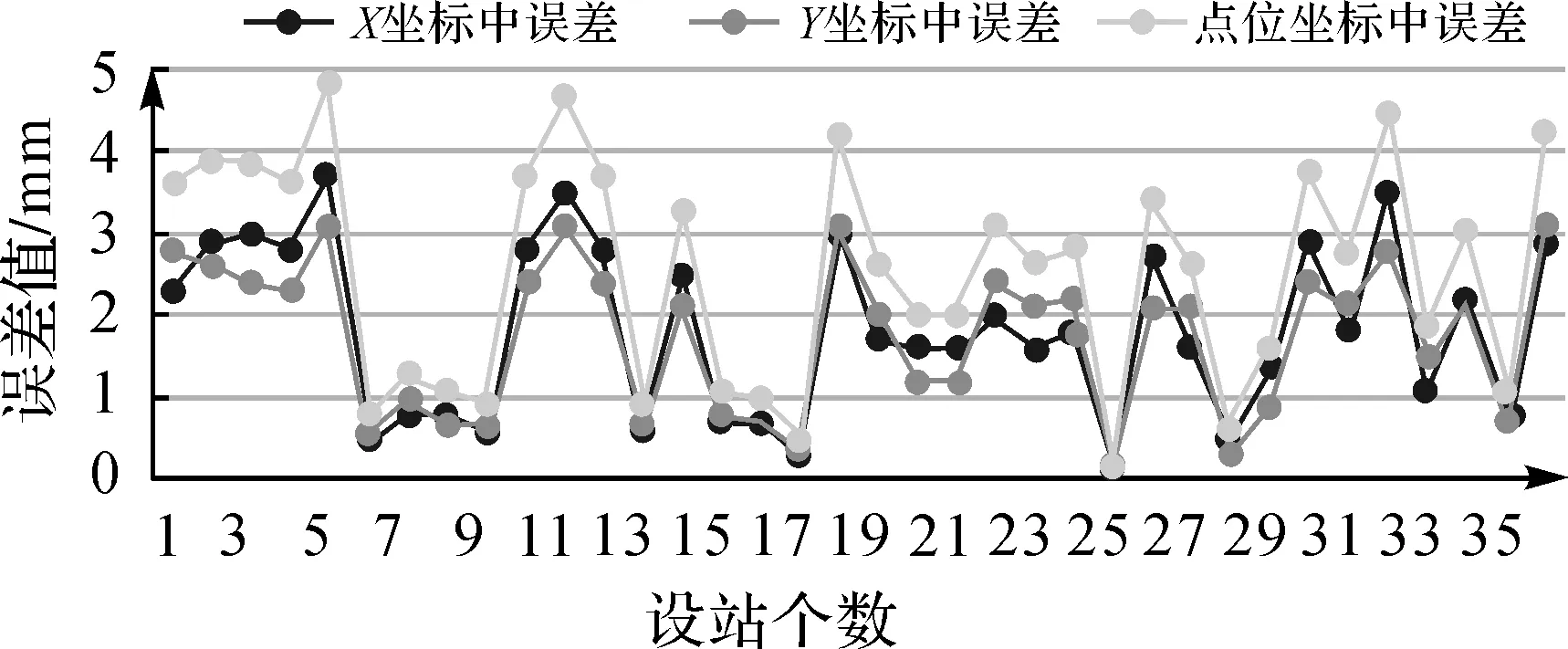
图6 自由设站测量X、Y坐标中误差及点位中误差分布
由图6可知,全站仪自由设站测量X、Y坐标中误差及点位中误差全部小于5 mm,且大部分小于3 mm,说明该大桥平面控制网精度等级高,自由设站测量精度高,能够获取高精度的主梁测点坐标,可以满足大跨斜拉桥主梁平面施工监控测量的精度要求。
2.2 基于间接高差传递方法的主梁竖向线形测量及精度分析
该桥主梁竖向线形的测量,首先采用图2所示的中间法三角高程将岸测的高程起算点A传递到主梁0#块附近索塔侧壁上的B点,作为主梁竖向线形测控的起算高程。区别于传统的主梁竖向线形测控(二等水准测量)方法,笔者提出采用高精度全站仪间接高差法进行该桥主梁竖向线形的测量,并将测量结果与二等水准测量结果进行对比分析,从而验证本文方法的正确性。全站仪间接高差测量测点高程的原理和主要步骤分别为:
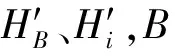
(12)
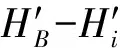
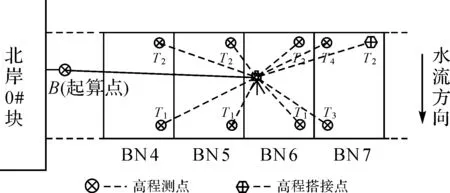
图7 全站仪间接高差测量主梁竖向线形方法
(3) 为了保证主梁竖向线形测量结果的正确性,上述一个测站的测量工作完成后,将全站仪在原测站附近重新设站,并重复上述步骤(1)和步骤(2),则每个测点高程值被测量两次,若两次测量的高程较差在±2 mm内,则满足设定的精度要求,可取两次测量的高程均值作为主梁竖向线形施工监控的依据。
(4) 随着施工的持续进行,主梁节段数量增加,全站仪到索塔壁高程起算点B的距离越来越大,而全站仪到测点的距离相对较小,此时若采用索塔侧壁上的B点进行间接高差传递测量,必定会引起较大的测量误差。为此可以在待测点附近设置一个棱镜转点,如图8所示,首先通过中间法三角高程测量将B点高程传递到棱镜转点,得到棱镜转点中心高程值,作为主梁监测点的高程起算值,再按照步骤(1)—步骤(3)即可得到准确的测点高程。
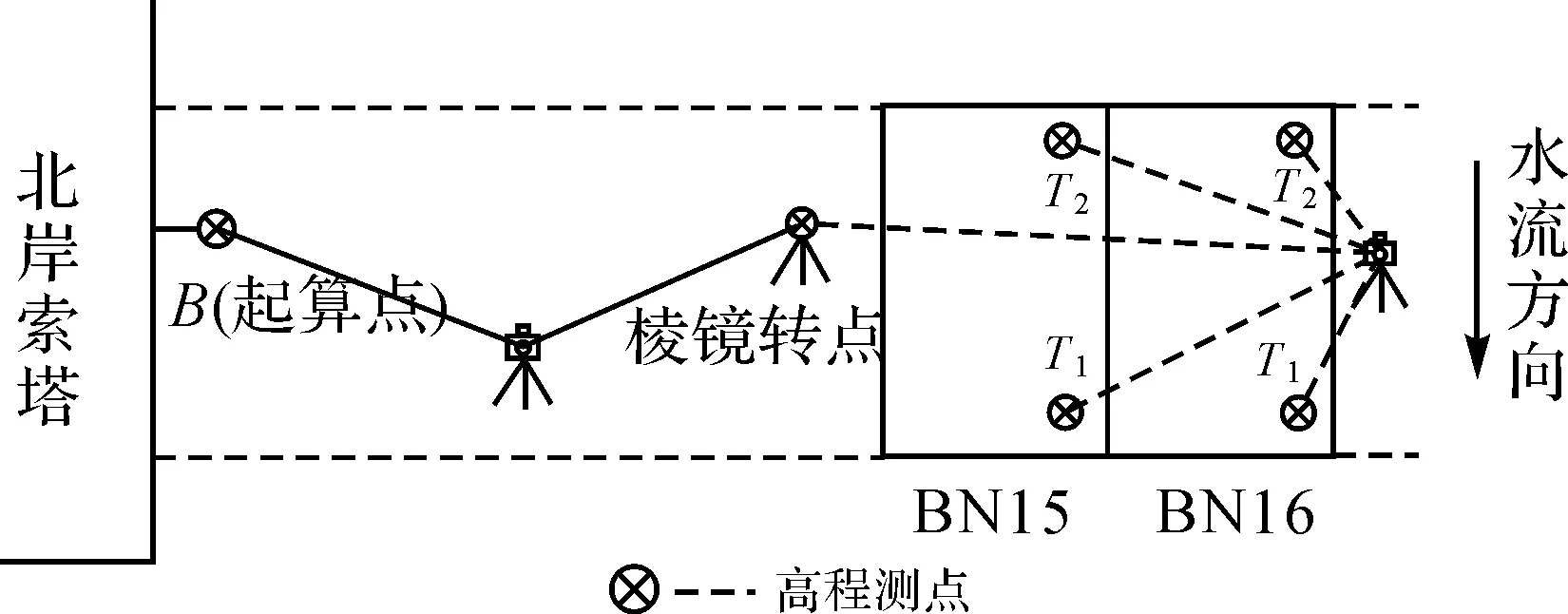
图8 传递起算点高程的主梁竖向线形测量方法
为了验证采用全站仪间接高差测量主梁上测点高程的准确性,在施工现场采用全站仪间接高差测量测点高程的同时,还采用电子水准仪对同一个测点进行二等水准测量。两种不同测量方法的起算点均为图2中索塔侧壁上的B点,由于B点采用了图3所示的测量标志,因此两种测量方法的起算高程不存在误差。本文选取北岸索塔边跨LB8—LB4节段测点进行了验证对比测量,表1为两种方法测量结果的对比情况。
由表1可知,两种不同测量方法得到的高程互差绝对值全部在1 mm内,且互差绝对值在0.6 mm以下的占71.43%。因此采用全站仪间接高差测量测点的高程精度高,结果可靠,能够满足主梁竖向线形测量的精度要求。通过施工现场试验还证明,采用全站仪间接高差的测量方法不需要频繁搬站,测量视线不易受桥面复杂的环境干扰,测量效率远高于水准测量方法,便于夜间测量。
表1 全站仪间接高差测量测点高程与二等电子水准测量结果对比
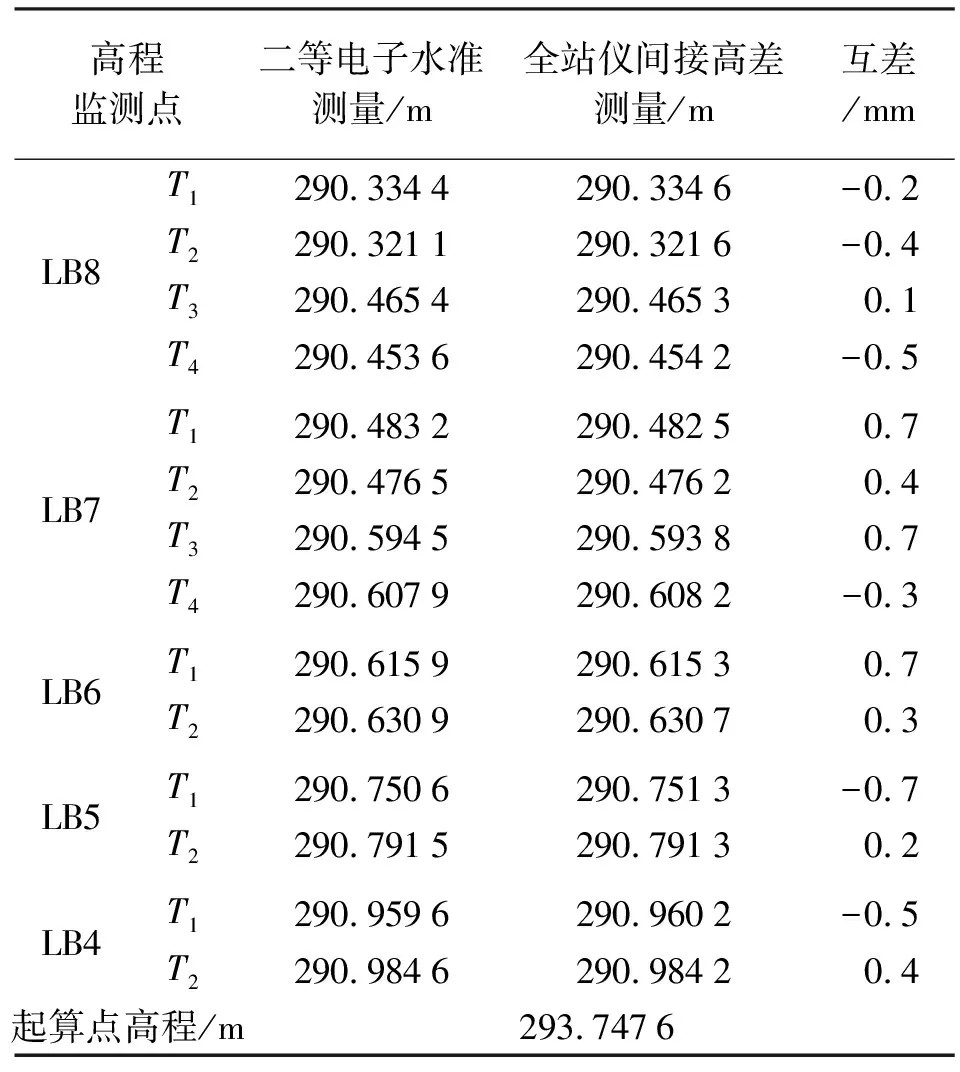
高程监测点二等电子水准测量/m全站仪间接高差测量/m互差/mmLB8T1290.3344290.3346-0.2T2290.3211290.3216-0.4T3290.4654290.46530.1T4290.4536290.4542-0.5LB7T1290.4832290.4825 0.7T2290.4765290.47620.4T3290.5945290.59380.7T4290.6079290.6082-0.3LB6T1290.6159290.6153 0.7T2290.6309290.63070.3LB5T1290.7506290.7513-0.7T2290.7915290.79130.2LB4T1290.9596290.9602-0.5T2290.9846290.98420.4起算点高程/m293.7476
3 结 论
通过本文对大跨径斜拉桥主梁线形测控方法的研究,取得一些创新并得到以下结论:
(1) 对于大跨径斜拉桥主梁平面线形的测量,可采用全站仪自由设站法测定主梁测点的平面坐标,测量检核条件多、精度高,测站位置灵活,不易受现场施工复杂环境的影响。
(2) 对于大跨径斜拉桥主梁竖向线形的测量,可采用全站仪间接高差法,其测量精度可达二等水准测量要求,测量视线不易受桥面复杂的环境干扰,测量效率远高于水准测量方法,便于夜间测量。
(3) 全站仪间接高差法测量测点高程时,将全站仪的“便利高”输入到全站仪中,则从全站仪中可直接得到测点的绝对高程值,无需后处理过程,便于现场的测量工作。
(4) 随着主梁节段数的增加,若悬臂端主梁高程测点距离零号块上的工作基点较远,可在合适位置放置棱镜转点, 首先通过中间法三角高程测量将工作基点高程传递到棱镜转点,再按照间接高差法即可准确测量测点的高程。
(5) 本文首次将全站仪自由设站和间接高差测量法应用在大跨斜拉桥主梁节段线形测量中,取得了较好的测量效果,值得在同类工程中推广。

