双曲镜面成像单目全景感知三维重构技术研究

郭伟青,汤一平,袁公萍,鲁少辉,陈 麒

1(浙江工业大学 信息工程学院,杭州 310023)2(浙江工业大学 之江学院,浙江 绍兴 312030)

1 引 言

全景立体感知三维测量与三维重构,是一门新兴的、极具发展潜力和实用价值的技术,可被广泛应用于航空航天、医学诊疗、机器人视觉、工业检测、虚拟现实、地理勘测、动漫影视等众多领域.基于镜面成像技术获取被测物体或场景的三维信息,可降低信息获取的成本,增加信息获取的实时性和同步性.镜面成像系统使用方便、信息丰富,在全景立体感知三维测量及重构的研究中被越来越多的研究者所关注,已成为计算机视觉和计算机图形学领域的研究热点[1].

曲面镜成像根据曲面的曲率来改变空间显示,曲面镜成像系统的主要优点是可以获取比使用平面镜成像系统更大的视野,且耗费成本低,同时畸变范围可接受[2].

单曲面镜成像系统常用于全景成像,如机器人导航、会议技术、多照片的全方位成像、全景重构等.该类系统的研究关键是选取合适的镜面形状,相机可置于椭圆形或双曲线形镜面的一个焦点处,或置于圆锥曲线的投影中心点.研究者通常采用单一投影中心点的投影系统,来获取合适的投影视图.文献[3]设计的全方位三维成像系统,由一个双曲面镜、CCD摄像头、衍射光学元件DOE和红外激光二极管构成,三维深度信息通过深度测量模型获取,采用序列编码算法和点阵图案找到两个图像中的对应斑点,用于计算目标图像和参考图像间的移位散斑.Sooyeong Yi[4]等提出利用激光和圆柱形透镜来实现全景三维测量的方法,能使光源覆盖较大区域,但激光与圆柱形透镜的组合会削弱光能量密度.文献[5]根据全景成像获取像素点显示的光源颜色信息,采用颜色识别算法以及几何对应关系进行图像特征点的立体匹配和空间物点的深度值测量.Chi Zhang[6]等使用投影仪和双曲面镜组合设计了一组全景投影装置,该装置与全景视觉传感器垂直放置,得到三维视觉传感器,实现被测物体某个面上物点的深度检测.文献[7]根据双曲面镜成像原理,利用带有全景视觉传感装置的爬行机器人,获取管道内壁的全景信息,检测出管道内壁缺陷并重构出三角网格模型,该方法在处理非均匀截面采样点数据时易出现形状的失真和不稳定.文献[8]提出了一种基于双曲面镜全景成像的隧道内壁三维检测方法.对隧道横断面进行全景扫描,获取隧道切面全景扫描图像,根据标定结果解析出隧道内壁的三维信息,该方法局限于三维点云的显示,未实现三维几何模型的重构,不具有可编辑性.

单曲面镜多反射成像系统,即万花筒成像系统,该类系统具有一维连续性,其它维度均得到离散的视点,常使用带有内部高光的圆锥镜面,主要应用于深度估计和全方位纹理识别[9],该类系统的镜面截面信息采用光路展开过程进行分析.

曲面镜成像产生曲面变形是不可避免的一个问题.为了获取合适的投影效果,研究者对成像系统的镜面形状进行了优化[10].如在成像坐标与光线入射角之间设定一种线性关系,通过折反射成像系统可获取图像中坐标系的线性关系.镜面形状优化包括非畸变的广角视图获取、域定义投影模式获取、最小化图像空间误差.通过解最小化误差函数或微分方程,对曲面镜的导数属性进行描述,并扩展应用于镜面折反射成像系统.

多曲面镜成像系统常采用球面镜队列和球冠队列[11,12].文献[11]中场景照明的入射光线采用球面镜队列来获取,空间和方向的变化照明被用于重构场景,并计算深度映射和重聚焦操作.文献[12]提出了一种自动架构用于竖直校准球面全景成像,使用场景中的水平和垂直线定义一个成本函数用于竖直校准,产生所需视觉效果,用于各种场景的球面全景成像.球冠减少了球面边界的不可用区域,球冠队列常用于光场成像和三维重构.多曲面镜成像系统需避免镜面间的相互反射,对图像的相应区域的分解作分析较复杂.

本文针对基于单目全景立体感知的被测物体或场景三维建模问题,通过研究单目单视点折反射全景成像机理,利用二次双曲面镜的光学特性,设计具有统一摄像机内部参数和颜色系统的全景感知系统,实现一种单目全景立体感知三维测量与三维重构方法.该方法利用双曲面镜成像技术获取被测物体的激光反射点,得到被测物体全景切面扫描图像,利用空间几何约束关系,获取被测物体内表面的三维采样点数据,对采样点进行柔性B样条曲面拟合,实现被测物体的三维几何模型重建.与同类研究文献[7,8]相比,采用改进的柔性B样条插值,对正常形貌区域的建模通过柔性节点矢量的控制,以减少控制点,对非正常形貌区域通过柔性插值B样条曲面,以增加控制点,凸显变形或奇异区域,便于后续甄别和诊断缺陷.改进在拟合非均匀成像采样点时形状的失真和运算不稳定现象,避免控制点的大量增加,且具有局部可控性.

2 双曲镜面单目全景成像原理

2.1 镜面折反射成像

镜面折反射成像主要由折射光学设备(透视摄像机)和反射光学设备(镜面)组成.将反射镜面置于摄像机轴向方向,使周围360°场景中的入射光线经反射镜反射汇聚于透视摄像机的光心,形成全景图.反射镜面主要包括双曲面镜、球面镜、椭球面镜、抛物面镜和圆锥面镜等;根据折反射系统是否满足单视点成像约束,Nayar S K等[13]将折反射成像分为单视点成像和非单视点成像,提出完全满足单视点约束的折反射系统有两种:一种是由远心透镜摄像机及抛物面反射镜构成,另一种由普通摄像机和双曲面反射镜构成.单视点成像约束属性是指被测场景中物点反射的光线经镜面反射后可汇聚于一点,称之为单视点.

单视点约束使得像机投影成像为透视投影成像,被测物体或场景上任一点在成像平面上的成像点是唯一的.采用已知成像模型的相关参数,可从透视投影成像中通过逆运算获取空间点三维坐标.在对被测物体或场景的测量与重建中,使用单摄像机和双曲面镜构成全景视觉系统,满足单视点约束,同时扩大可视范围,本文的全景视觉传感系统采用了双曲镜面的折反射成像.

2.2 单目全景成像原理

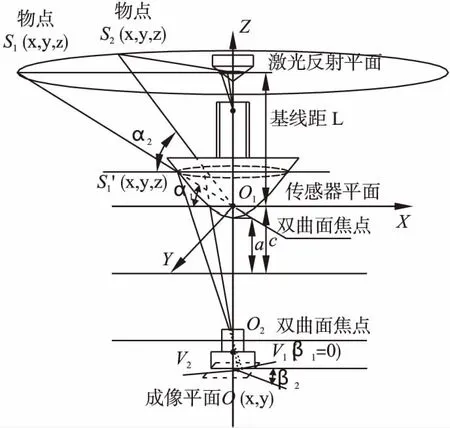
图1 双曲镜面单目全景成像原理图Fig.1 Monocular panoramic imaging principle of an hyperboloid

双曲镜面成像满足下列双曲线方程:

(Z-c)2/(b2)-X2+Y2/a2=1

(1)

a2+b2=c2

(2)

式中X,Y,Z为双曲镜面上的空间点坐标;c为双曲镜面的半焦距距离;a,b表示双曲镜面的实半轴和虚半轴长度.

由于双曲镜面的旋转对称性以及受曲率的影响,全景图中有效的成像部分是一个圆形的对周围场景及物体进行显示的畸变图像,它包含了周围360°范围的信息,图2为拍摄的全景图.

图2 全景图Fig.2 Panorama

为找出单视点相机拍摄的全景激光图中激光点与所对应的实际空间坐标之间的关系,本文根据Scaramuzza D[14]展开式方法标定全景成像系统,其标定参数见表1.入射角α由公式(3)求出.

(3)

式中‖u″‖表示激光反射光线在传感器平面XY的投影点离O1的像素距离;f(‖u″‖)为平面点与实际空间点之间的对应关系;a0,a1,a2,…,aN为全景成像系统的标定参数.传感器平面像素点与成像平面像素点的对应关系用公式(4)表示:

u″=Au′+t

(4)

式中A∈R2×2,t∈R2×1,u″表示物点S在传感器平面XY的投影像素点,u′表示该物点对应的成像平面xy上像素点,则成像平面xy上各像素点和相应入射角α的对应关系可使用公式(3)、公式(4)求得.全景成像系统的标定算法参见文献[14].依据公式(4),由标定参数及成像平面xy上的像素点坐标可计算出其对应的传感器平面XY上的点坐标u″=[u″,v″]T,再依据公式(5),可求出其对应的方位角β.

(5)

表1 全景成像标定参数
Table 1 Calibration parameters of panoramic imaging

CalibrationParametera0a1a2a3a4AtCenterPointvalule-110.2100.0000.00230.0000.9999-10.1e-005-9.1e-0051[]49.461-15.692[]587.096348.682[]

3 全景成像激光中心线的提取

全景成像标定精度和激光中心点精度决定了入射角α的计算精度,故从全景截面扫描图中准确提取激光中心线是全景成像三维测量和重构的关键.

影响激光中心线提取精度的噪声主要包括:图像采集系统噪声及激光散斑噪声.前者产生的主要原因是相机传感器异常或存储传输错误等问题引起;后者产生的主要原因是激光投射到物点经漫反射后产生的无规律分布的暗斑和亮斑.全景成像受噪声影响的灰度值如公式(6)所示:

Iim(u′,v′)=Ila(u′,v′)θsp(u′,v′)+In(u′,v′)

(6)

式中,Ila(u′,v′)为无激光散斑噪声干扰时的激光灰度值;θsp(u′,v′)为散斑对比度,该散斑取样以成像平面上像素点(u′,v′)为中心,以m*n为取样区域范围;In(u′,v′)为全景成像系统图像采集噪声.

本文采用中值滤波降低噪声干扰.实验中,同一位置滤噪前后激光线放大对比如图3所示,从图中可见,通过滤噪处理后图像保留了尖锐边缘,并选取适合的点取代孤立噪点,滤噪效果较好.

图3 滤噪前后的对比图Fig.3 Comparison diagram of before and after filtering

全景成像系统将激光投射至被测场景内壁,该激光线经内壁反射后在成像平面成像,图像中的激光条纹理论上是一条宽度仅为单像素的单线,但因激光发射器的发散、锥体表面漫反射等因素,导致成像条纹具有多个像素宽度.为准确获取条纹中心点,需将条纹细化为无宽度坐标,用于三维点云的计算.

根据激光反射光带亮度满足高斯分布的特性,本文采用了高斯曲线拟合和Bezier曲线提取全景激光条纹的亚像素中心点,具体实现过程如下:

Step 1.以全景图像的中心坐标O(uo,vo)为极点,水平向右为极轴,逆时针方向为正方向建立极坐标系.

Step 2.初始化方位角β=0,计算β方向激光中心点坐标.取步长=1,沿β向遍历,记录离极点O距离为ρk的像素点的亮度值Ik,k=1,2,…,n,对非整型坐标用双线性内插法计算其亮度值.然后计算从距离为ρk的点开始的s个连续像素点的亮度值和,记录总和最大时的起始点对应的像素距离ρmax,利用高斯曲线拟合该s个像素点的亮度值,拟合所得曲线的极值点所对应的像素距离为ρc,具体计算方法如公式(7)～公式(10)所示.

(7)

ZS×1=[lnI(ρi) lnI(ρi+1) … lnI(ρi+s-1)]T

(8)

A=[a0a1a2]T=(XTX)-1XTZ

(9)

(10)

式中,S为需要拟合的像素点个数,实际系统取值为5,ρi为某点离中心极点O的像素距离,I为该点的亮度值,ρc为激光中心点离极点O的像素距离.

Step 3.0→2π范围内计算各β方向激光中心点坐标.当所提取的激光点数为n,则对方位角β以增量△=2π/n,从0→2π遍历得到各β方向上的像素距离ρ.

Step 4.提取激光中心线.Step 3中仅通过径向亮度信息,计算出像素距离,得到所对应的激光中心点,未考虑相邻的激光中心点间的连续性,会导致突兀点的出现.本文对相邻激光中心点的像素距离采用Bezier曲线进行平滑处理.首先获取当前β方向的像素距离ρm和相邻两方向的像素距离ρm-1、ρm+1,由公式(11)得出当前像素距离的理论值L,当|ρm-L|<阈值限定,则ρm=L,反之则判定为突兀点,丢弃该点.直到所有激光中心点处理完成.

L=(1-t)2ρm-1+2t(1-t)ρm+t2ρm+1t∈[0,1]

(11)

上式中t为取值范围0-1的常量,实验中取值t为0.2.

Step 5.根据提取出的n个不同β方向上的激光中心点离极点O的像素距离ρ,将其转换为图像坐标系下的坐标点P(u,v).

4 全景成像中三维点云数据的获取

采用全景视觉传感装置获取被测场景内壁全景切面扫描图像,提取激光中心线,解析出各截面的激光投射点位置信息后,可计算场景内表面三维点云坐标.以双曲面焦点O为原点建立高斯坐标系,物点的三维空间信息可用(α,β,ρ)来确定,如图4所示.对于物点S,令ρs为S到O的距离;αs为S到O的入射角;βs为S到O的方位角,L为S点到O之间在Z轴的投影距离,即基线距.高斯坐标的αs和ρs由公式(12)给出:

(12)

式中,‖u″‖s为S点对应于成像平面上的点到成像平面中心点的距离,方位角βs通过公式(5)计算求得.

图4 三维点云几何测量原理图Fig.4 Principle diagram of 3d point cloud geometry measurement

根据计算出的物点空间几何信息,将物点用笛卡尔坐标系S(x,y,z)来表示,以便进行全景成像三维几何模型重构,其计算方法由公式(13)给出.

(13)

式中Δz为相邻全景激光投影平面之间的距离.在被测物体的测量中,激光平面沿着Z轴方向随着全景成像装置的移动,其位移量为Δz=zi-zi-1,i=1…N,单目摄像机依次记录下N个激光切片图像序列.

5 基于点云数据的三维几何建模

为了重构出被测物体三维几何模型,我们从上述N个切片图像上获取三维点云数据后,采用了B样条柔性插值方法来实现几何模型重构.

采用改进的柔性B样条插值,对正常形貌区域成像采样点的重构,通过柔性节点矢量的控制,以减少控制点,对非正常形貌区域成像采样点重构通过柔性插值B样条曲面,以增加控制点,凸显变形或奇异区域,便于后续甄别和诊断缺陷.

5.1 B样条曲面

B样条因其具有局部可调性以及节点矢量的依赖性而成为参数曲面拟合的主要方法[15].B样条参数曲面的定义如下:

(14)

其中(m+1)*(n+1)个控制顶点Pi,j构成四边域控制网格,Ni,p(u)、Nj,q(v)表示u方向、v方向的p次、q次B样条基函数,U和V为节点矢量,其表示形式如下:

(15)

(16)

B样条曲面拟合的前提是进行曲线拟合,B样条曲线拟合可采用曲线插值或逼近来生成一条靠近已知数据点的曲线,其过程包括以下几方面:确定型值点参数;选择节点矢量;计算控制顶点.下面对上述步骤作一分析.

5.2 B样条曲线拟合

已知n+1个截面采样点数据C,以及待求的参数T和节点矢量U,p次B样条曲线满足下式:

(17)

若每个截面采样点都对应一个参数ti,则可用一组线性方程表示,其矩阵形式如下:

[C]= [N][P]

(18)

[C]为已知截面数据点的(n+1)*3矩阵,[N]表示B样条基函数的系数矩阵(n+1)*(n+1),[P]表示未知控制顶点的(n+1)*3矩阵.

曲线曲面的形状最终是由控制顶点来决定,为了获取理想的控制顶点,需求出合适的参数值T和节点矢量U.

5.3 型值点参数的求取和节点矢量的计算

型值点对应的参数值和节点矢量的取值影响曲线的形状.本文采用累积弦长参数化方法,该方法的参数值遵循原始型值点的分布,其计算过程如下:

(19)

其中ti为第i个参数值,d为总弦长.其流程可表述为:

Step 1.输入已知数据:

参数值T={t0,…,tn};n是截面数据点最大下标;p是曲线阶次;

Step 2.赋值u0=…up=t0,赋值un+1=…=un+p+1=tn;

Step 3.j从1到n-p循环执行

sum = 0;

i从j到j+p-1循环执行

sum +=ti;

uj+p= sum/(double)p;

结束j循环;

Step 4.输出计算结果:

节点矢量U={u0,…,un+p+1}.

5.4 柔性节点矢量的选择

在曲线拟合过程中,由于B样条曲线的局部可调性,使得节点矢量的取值在一定范围内可作柔性调整,而不会导致运算的不稳定及曲线形状的失真.在算法中设置柔性间距阈值限定,在阈值限定范围内节点值可作相应的调整,可表示为:

(20)

其中up、up-1分别表示阶次为p和p-1的节点矢量,p阶曲线的节点值在p-1阶曲线的相邻两个节点值之间,我们设定柔性间距百分比为Rate,用以调整间距的范围,若Rate取值为0,则p次节点矢量被选中,若Rate取值为100%,则p-1次取值范围内的所有节点值都可作为被选择的域节点.

5.5 B样条曲面拟合

根据上述柔性节点矢量选择拟合而成的曲线来进行B样条曲面插值,可得到阶次为p,q的连续B样条曲面.算法如下所述:

Step 1.输入已知数据:

截面数据点Ci,ji=0…n;j=0…mi;

截面数据点的行数n,每行数据点数mi;

p,q是曲面在u和v方向的阶次;

Step 2.找出数据点数mi最大的行;

计算该行参数值T={t0,…,tmi};

i从0 到n循环执行

拟合Ci(v);

结束i循环;

Step 4.使用曲线Ci(v)的控制顶点作为u方向的数据点;

s从0到n循环执行

曲线Cs(v)的第k个控制点赋值为Rs

结束s循环

结束k循环

Step 6.依据控制顶点Pk,s和节点矢量U、V得到拟合而成的曲面S(u,v);

Step 7.输出计算结果:

拟合而成的曲面S(u,v)以及曲面控制顶点P.

6 实验论证

为获取实验的图像数据,我们采用分辨率为1280×720像素的摄像头,并将摄像头与全景视觉传感器同轴放置,连接成一个整体,双曲镜面参数取值a=50mm、c=60mm,其视场范围360°×120°.将全景视觉传感器与PC机连接,用PC机实现被测场景三维图像的采集、处理及存储,PC机的CPU主频为2.7GHz、内存为4G,操作系统为Windows7,用Java语言编程实现.

实验选取了三个检测对象:即内径Ф=600mm标准圆形管道、同内径圆形形变管道和U形管道.

圆形管道实验环境如图5(a)所示.将全景成像装置放置在管道中心位置,该装置沿Z轴方向匀速向前行进,摄像单元获取激光切片全景图像序列,图像样本数为30幅.图5(b)为拍摄的全景激光切片图、图5(c)为提取出的激光中心线图.图5(d)、图5(e)分别为管道内壁点云显示图和B样条曲面拟合后的管道重构图,图5(f)为渲染后的三维效果图.图5(g)-图5(i)为圆形变形管道实验图例,图6为U形管道实验图例.实验结果显示,本文实现的单目全景成像三维重构方法能有效获取被测管道内壁的全景空间信息,并重构出管道的三维几何模型.

图5 圆形及形变管道实验示例图Fig.5 Circular pipe and distorted pipe experimental example diagram

图6 U形管道实验示例图Fig.6 U-shape pipe experimental example diagram

为验证本文算法的测量精度,在半径为300mm、横截面积为282700mm2的标准圆形管道内进行了半径测量实验,实验按序选取20帧截面,每帧截面按方位角递增序采样1000个点,根据采样点求出各截面平均半径和横截面积.横截面积计算是将相邻两个采样点和圆心坐标构成的三角形作为面积单元,计算单元面积并遍历一周累加得到当前截面的面积.实验结果如表2所示.其中“+”表示大于理想值“-”表示小于理想值,从实验结果可以看出,利用本文方法测量半径和横截面积的精度达到97%以上,表明该方法能较好地满足测量及重构的精度要求,但测量精度在不同程度上受多个因素的影响,包括双曲镜面加工误差、标定误差、激光光源的全景投射误差、用于激光折反射的圆锥面加工误差、基线距设置误差等,这些都会引起系统的测量和重构误差,因此,从以上几个方面进一步改善系统可以提高重构精确度.

表2 管道半径和横截面积测量实验结果
Table 2 Pipe radius and cross-sectional area measured experimental results

截面号测量平均半径(mm)半径测量误差率(%)测量横截面积(mm2)横截面积测量误差率(%)1297.8-0.7491278855-1.40732296.4-1.1923276142-2.34023296.3-1.2233275899-2.45514297.2-0.9271277540-1.85225297.2-0.9271277583-1.85226297.1-0.9799277216-1.97597297.7-0.7831279399-1.22468296.3-1.2420275797-2.48029296.4-1.2154276297-2.321310296.4-1.2154276296-2.321311296.9-1.0305278496-1.529012296.4-1.1869277704-1.778013296.8-1.0781276662-2.166014296.8-1.0781276664-2.166015296.6-1.1219277037-2.031916296.5-1.1584276200-2.322317296.5-1.1584276208-2.322318296.3-1.2231277310-1.932919295.8-1.4080275373-2.628420295.7-1.4255275418-2.5957

7 结 论

本文通过研究单目单视点折反射全景成像机理,利用二次双曲面镜的光学特性,实现一种全景立体感知三维测量及重构方法.利用全景成像技术获取被测物体的激光反射点,得到被测物体全景切面扫描图像,利用空间几何约束关系获取被测物体表面的采样点数据,对采样点进行B样条曲面柔性拟合,改进通用重构方法在拟合非均匀采样点时形状的失真以及运算不稳定现象,避免控制点的大量增加,快速实现被测物体的三维重建,该方法可适用于管道隧道地下交通设施等的检测及重构.为验证本文方法的有效性,进行了标准管道和形变管道以及U型管道的重构实验,并对标准管道进行了精度测试,实验结果表明本文采用的方法是有效可行的.