边缘计算下的多无人机野外协同作业机制研究
季鹏飞,徐曾春,胡 平
(南京工业大学 计算机科学与技术学院,南京 211816)
1 引 言
目前,无人机以其快速、机动、灵活等优点被广泛地应用于测绘,航拍,救灾等领域.随着科技的发展,其运用方式从最初的单机任务向多驾无人机组成编队协同完成任务发展[1].如何对无人机编队进行统一管理、合理调度,使其快速高效地完成作业任务是无人机研究的关键问题之一[2].
在无人机编队执行野外搜救任务时,疑似目标在地面的分布是随机的,不可预知的,这就意味着同一时间无人机网络中的各节点负载极有可能是不均衡的,这可能导致部分无人机长时间过载提前耗尽能量,进而影响整个编队的续航.通过任务间卸载调度使各节点互相帮助,可以实现节点之间的负载均衡.但无人机编队的调度多依赖于云台控制,在野外的通信环境中可能难以连接到云台,边缘计算模型可以为该问题提供解决方案.边缘计算是指在网络边缘执行计算的一种新型计算模型,其基本理念是将计算任务在接近数据源的计算资源上运行.边缘计算模型将原有云计算中心的部分或全部计算任务迁移到数据源的附近执行[3].
本研究的核心问题是在纯边缘环境中为无人机节点间的可卸载作业做出调度决策.在做出调度决策之前,需要确定哪些节点的状态信息(NSI,node status information)需要共享以及共享的频率.但这并不是说无人机在作业时必须进行任务卸载,这要看把任务卸载给其他邻节点能否给自身带来时间或能耗上的收益[4].本文使用排队论使底层硬件的调度算法抽象化,假设系统由中央处理器(CPU)节点或专用加速器(如图形处理器和FPGA)组成,避免了为每项任务做出决策的需要,提出了一个纯粹的边缘分布式解决方案,其中节点只需要与跟它们直连的相邻节点通信.根据求解程序的执行位置以及数据共享方式的不同,提出了四种算法,并将其性能与非协作情况进行比较.总之,本文的主要贡献如下:
1)针对无人机自组网络中的边缘分布式系统提出了用于实时工作负载均衡的新算法.
2)制定了包含电池电量、链路带宽和CPU可用性等节点状态信息(NSI)的卸载成本函数.
3)设计了可模拟无人机工作过程的模拟器.
4)与非协作(NC)系统相比,验证了所提出的算法改进了无人机自组网络系统的性能.
第2节介绍相关工作,第3节使用队列网络对无人机网络进行建模并正式定义问题.第4节详细介绍了提出的负载均衡算法.第5节中描述了实验设置和仿真结果.最后进行总结和展望.
2 相关工作
多无人机协同系统本质上是任务分配和资源调度的问题.解决问题的核心是合理建模和优化.针对这一问题,目前有一些相关研究.例如Li等人[5]提出了一种多无人机协同侦察任务规划模型MPCU,采用遗传算法对模型进行优化.Gu等人[6]提出了基于动物群体感知方法的多无人机协同资源调度和任务分配方案.Denis等人[7]提出了面向无人机编队实时任务调度的网络中心多智能体系统.考虑了初始调度和动态重新调度两部分.Simi等人[8]为多无人机网络提出了一种分布式任务分配算法,使用动力感知协调和规划方法来协调多个无人机的活动.但是这些研究都存在以下不足:1)研究的基础都不同程度地依赖云端的计算能力,这就要求无人机与云端之间有可用的通信链路,而这样的通信条件在无人机野外或灾后作业中可能无法满足.2)相关文献中,单个无人机在任务分配后只完成自己分配到的任务,无人机间不存在单个任务拆分卸载后共同完成的行为.各节点间只有信息交互,而没有任务处理方面的互相帮助.3)在任务分配调度过程中没有充分考虑无人机的实时能量状态和计算能力.这可能加剧节点间的任务负载不均衡,进而使部分无人机能量提前耗尽退出编队,打乱原有计划.
针对以上不足,本文提出了一种基于边缘计算的多机协同互助作业方案.该方案与普通边缘计算方案有所区别,普通边缘计算方案多是云雾地三层架构[9],在云层和底层设备间构建中间雾层提供缓存和计算服务.本文重点研究当云层和雾层能提供的计算能力很弱甚至完全不可用时如何在真正处于最边缘的设备(无人机)上完成作业的方案,并且将能耗作为一个重要指标纳入算法考核范围.
3 系统建模
图1是一个无人机搜救编队,当执行搜救任务时,无人机编队在事发区域内按照事先规划的航线飞行搜索,因为无人机飞行时需要不断对疑似目标进行识别且各无人机的视场角叠加后需要完全覆盖当前工作区域,所以编队内各无人机飞行速度不能过快且间隔距离不能过远.对无人机网络进行建模.建立如下关系:
G=(N,A)
其中,G是一个有向网络,N是n个节点的集合,A是m个有向弧的集合.弧(i,j)∈A代表从节点i到节点j的一条通信链路(例如Wi-Fi),并且有一个相关的成本函数Cij表示该弧上每单位流量的成本.

图1 无人机搜救编队Fig.1 UAV search and rescue formation
3.1 节点
每个节点都是一个带有CPU,Wi-Fi,摄像头等传感设备的无人机.使用M/M/1队列来对其中每个模块的工作进行建模.M/M/1具有先到先服务(FCFS)调度规则,任务到达过程是泊松过程并且服务时间呈指数分布[10].对于通信部分,同样使用两个M/M/1队列(发送方和接收方)对Wi-Fi模块进行建模,定义Wi-Fi发送、接收和传输速率相等(即μiWS=μiWR=μiWF).最终建模如图2所示,其中CPU,WR,WS分别代表CPU,Wi-Fi接收器和Wi-Fi发送器队列.每个节点可以被定义为一个数组{γi,γi0,μiCPU,μiWF} 其中γi是可卸载任务的速率,γi0是不可卸载任务的速率,μiCPU是CPU的服务率,μiWF是Wi-Fi传输速率,本文将这些节点信息定义为节点状态信息(NSI).每个在无人机视野范围内出现的疑似目标都会生成一个可卸载的任务.节点本身必须自己完成的任务(如操作系统)和不能从卸载中受益的任务被归为不可卸载任务.

图2 无人机节点建模为队列网络Fig.2 UAV node modelled as network of queues
3.2 队列网络
如果有外部任务进入系统,则队列网络被定义为开放网络.这些网络可以使用Open Jackson网络进行建模[10].Vilaplana[11]将其用于建模云计算范例.Open Jackson网络指出队列a∈{1,…,k}的到达率可以由公式(1)给出,基于这个公式,可以计算系统中所有队列的任务到达率和任务输出率.
(1)
其中,γa是外部任务的到达率,λb是队列b的到达率,Pba一个任务从队列b移动到队列a的概率.
3.3 问题表述及定义
在无人机编队执行搜救或航测任务时,编队在指定区域内按照事先规划好的航线以中低速飞行搜索,整个过程中,编队队形基本不变,编队内各无人机节点间的相对运动速度很小[12].因此,无人机网络的拓扑结构基本稳定.本文将调度决策问题制定为最小成本流问题(方程2),约束条件是所有的任务都被调度,并且不会影响队列的稳定性.决策变量xij∈R(n×m)代表通信链路(i,j)∈A上的任务流.xii是本地处理的任务率.平均到达率小于平均服务率时,队列速率保持稳定.若节点中CPU队列的平均任务到达率大于其服务率,则需寻找替代方案.等式(2b)中的约束条件确保所有任务都被分配,而(2c)中的不等式约束确保任务可以被所分配到的相应节点处理.该公式使用来自所有节点的 NSI 并且同时对所有节点调度.该问题中的成本函数Cij在下文3.5节中具体描述.该最小成本流问题在每次有节点需要帮助时都会被执行,在执行该解算器前后,网络拓扑结构和通信成本不会发生明显变化.
(2a)
(2b)
方程(2)中的决策方案也可以用如下的决策矩阵定义:
(3)
定义矩阵X的每一行为决策向量(dv).决策向量dvi决定节点 i如何处理传入的任务.矩阵的第i列表示其他节点如何把任务卸载到节点i.
3.4 边缘分布式解决方案
考虑到任务到达率的时间变化性质,无人机编队需要频繁地解决方程(2)中的问题.下文5.1节指出,问题的复杂性取决于n(节点的总数)和m(弧的总数).所以可以通过原始分解来简化问题,由此每个节点计算自己的dv.这与Meskar[13]用于MCC 的类高斯-赛德尔方法相似.该方法主要与其最近的邻节点通信,以了解他们可以提供何种帮助并作出决策.这种方法不是自私地把所有任务都卸载给邻节点,它也考虑邻节点的计算资源,方程(4)为N中的每个节点i定义了这个问题.它与方程(2)中的中心问题不同,这里的每个节点i只根据从其近邻处可获得的信息尽量减少自身目标函数的成本.
(4a)
(4b)
3.5 成本函数
只要所有到达的任务都可以进行调度,即可保证所有队列速率稳定,我们希望以最小成本实现.定义如下的成本函数Cij作为从节点i调度单位任务到节点j的成本.
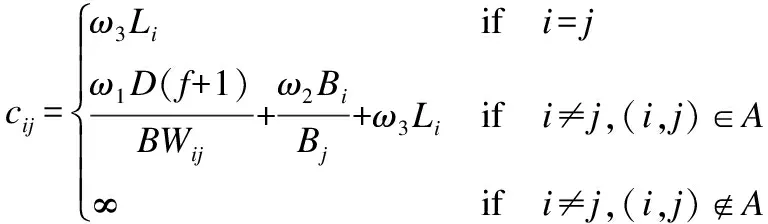
(5)
其中,D是数据量,f是平均重传次数(见公式6a),BWij是节点i和j之间的预期带宽,Bi,Bj是节点i和j中的剩余电量,Li和Lj是节点i和j中已有的任务量,ω1,ω2,ω3是权重因子.
成本包括三个不同的组成部分:通信成本、能量可用性以及CPU可用性.它们的重要性可以通过权重因子ω1,ω2和ω3来调整,在下面详细介绍.
1)通信成本
移动节点间的通信成本取决于两个节点间的预期带宽,数据量和信道环境,同时要考虑到两个节点间相对位移导致的链路生存时间变化,收发功率变化和多普勒频移等现象.本文中由于无人机编队内各节点的相对位移很小,所以链路和收发功率稳定,多普勒频移可以忽略不计.但由于各种噪声和干扰,通信信道不可能完美,本文使用重传因子f来描述信道环境.在实验中随机抽样两个节点之间的数据包投递率(PDR),并使用几何分布的均值来计算将数据从一个节点发送到另一个节点的平均传输次数(公式6a).这种关系(见图3)表明,随着PDR的降低,平均重传次数呈指数增长.通过仿真实验,发现0.5是建立有效通信链路的最低PDR.
f(PDR)=E[g(x;PDR)]
(6a)
g(x;PDR)=PDR(1-PDR)x-1,∀x∈{0,…,∞}
(6b)
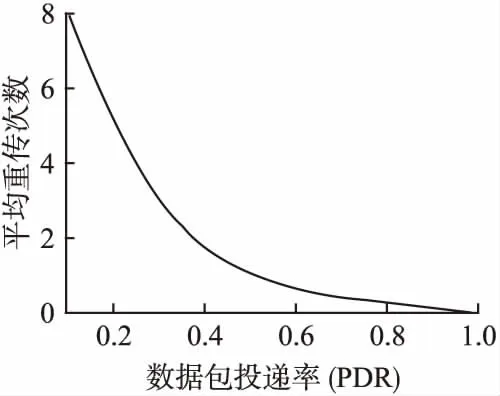
图3 在非理想信道下的平均重传次数Fig.3 Average no of retransmissions required due to imperfect channel
2)能量可用性
成本函数的第二个要素是节点的剩余能量水平,其重要性可以通过权重因子ω2来调整.在任务卸载调度过程中充分考虑节点的能量水平可避免木桶效应引发整个编队航程缩短,并且可以在一定程度上提高由电池供电的无人机电池的使用寿命.
3)CPU可用性
使用CPU队列中现有任务的数量来衡量CPU的可用性.较高的数字表明低可用性,反之亦然.这也适用于调度决策中的自我处理.
3.6 模拟器
本文使用模拟器进行仿真实验,在模拟器上可以为目标平台使用简化的算法流程模型,并根据需要更新组件.Wu等人用队列模型来模拟分布式节点的工作量[14].但他们假设节点在没有工作负载时不消耗能量,这在实际应用中是不现实的,本文对此进行改良.该模拟器的主要组件包含算法任务模拟,无人机功耗模拟和通信链路模拟等.
3.6.1 算法任务
算法任务的模拟器模型的特征是操作数(OP)、输入和输出数据量.例如人物检测算法输入尺寸为M×N的图像,每幅图像经过约C个OP后输出图像中的人数.假设每个时钟周期有一个OP,那么算法在无人机上的执行时间可以根据时钟频率估算.
(7)
在不同的处理器中,一个OP可能需要不止一个周期,一个周期也有可能有多个OP,但是这种近似的时间估计没有详细执行信息(公式(7)).在实际应用中,算法也可以先在测试设备(DUT)上执行以测量更精确地执行时间.
算法所需的操作数也不是一定的.例如在用于背景减除的梯度混合(MOG)算法中,操作数取决于检测特定像素的匹配高斯分布的速度[15].为了使计算更易模拟,本文采用未找到匹配高斯的最坏情况.
3.6.2 无人机功耗模拟
本文不考虑无人机的飞行动力能耗,因为本文的研究重点是无人机的任务计算能耗,飞行耗能是不可避免的.为了真实地模拟其行为,无人机被分为中央处理器(CPU)、图像传感器和WI-FI等模块,使用Jung等人的基于利用率的模型来计算能耗[16],相关参数可以针对不同的DUT进行设置和校准.
1)图像传感器
连续使用时,图像传感器在无人机中消耗大量能量.根据Likamwa等人,图像传感器每帧的能量消耗可以建模如下[17].
Ecamera=Pidle×(Tframe-Tactive)+Pactive×Tactive
(8a)
(8b)
由公式(8)可知降低图像分辨率可以降低Tactive,进而降低能耗,或者降低采样率也可达到同样目的.
2)处理器
CPU功率由闲时功率和运行功率两部分组成,如下所示:
(9)

CPU利用率根据使用时间与每帧可用时间的比率来计算.但操作系统(OS)和其他正在运行的应用程序也使用CPU.Dargie使用正态和指数分布来模拟工作量[18].我们也使用了一个随机变量r从高斯分布采样来模拟这些其他活动.通过调整r的均值可以模拟忙碌传感器和空闲传感器.总利用率计算如下:
(10a)
(10b)
其中N是要处理的算法的数量,Texeci是第i步算法的执行时间(如背景减除算法、人物检测算法等),TFrame是每帧可用时间.在检测算法特别复杂时有可能出现Texeci大于TFrame的情况,我们只运行CPU到100%的负载,并在下一帧运行算法的其余部分,依此类推.
3)Wi-Fi
Wi-Fi模型计算连接模式下Wi-Fi模块的时间和能量.根据不同的分组速率有如下两种模式.
(11)
其中pr是分组速率,βLT、βHT、βLT base和βHT base是文献[16]中的DUT参数.如果每秒的分组数超过阈值,则Wi-Fi处于高功率状态,否则处于低功率状态.功耗与数据速率成正比.本文不考虑Wi-Fi在扫描模式下的能量消耗,因为本研究的基础是无人机之间已经建立起连接.
4 均衡调度算法
上一节将任务卸载调度问题制定为中心式和分布式问题.本节定义一个协作环境,在该环境下所有节点都试图通过协作实现全局目标(即在分配的时间内处理尽可能多的任务).该环境下如果一个节点发送一个任务到另一个节点,另一个节点必须执行它.但也要考虑到节点不能是自私的,只有在有必要卸载时才卸载.考虑两种数据共享机制:主动式和反馈式.根据这些数据在节点之间共享的方式以及算法的执行位置不同,本文提出以下四种算法.并将这四种算法与非协作(NC)的情况进行比较.
4.1 Oracle式(O)
这是一个理想化的算法,Oracle可以全程访问所有无人机节点的NSI,每秒钟同时向所有节点发送dv.该算法解决了方程(2)中的成本最小化问题.这在实际应用中是不现实的,但它为其他算法的比较提供了最理想的结果.实验表明,即使忽略NSI的通信成本和执行解算器的成本,它的能量消耗也是最多的.
4.2 主动集中式(PC)
这是一个更为现实可行的Oracle版本.在该方法中指定其中一架无人机为服务器,其余所有节点将NSI发送给指定的服务器,然后解决方程(2)中的问题并将相应的决策向量dv发送回每个节点.在仿真实验中,服务器连接到所有节点,但这不是必需的,因为NSI和dv可以通过节点多跳传输.实验中考虑NSI的通信成本以及执行解算器的成本.在新的广播播出前,其他所有节点都必须遵循服务器做出的决策根据dv进行计算和卸载.我们希望找到最合适的广播NSI的频率以避免过勤广播浪费资源,但这个问题没有单一的答案,它取决于很多因素,如通信带宽,NSI的信息量大小,PDR和网络中节点的个数.如果有n-1个节点每隔t秒将NSI发送到服务器,忙碌概率最高的队列就是服务器的接收队列.分析其表现如下:
(12)
(13)
(14)
P[0]=1-ρ
(15)
其中,P[0]是队列中没有任务的概率.根据到达率和服务率,可以估计服务器接收队列的性能.例如,假设有11个无人机节点以54 Mbps的数据速率连接,PDR为0.7,NSI为1 Mbits,每10秒发送一次NSI.然后据公式(6a)估算队列利用率约为0.03,无需等待的时间约占97%.平均延迟约为0.03秒.图4显示了不同NSI更新频率和不同网络条件下的服务器队列利用率.

图4 服务器在各种网络环境和NSI更新频率下的队列利用率Fig.4 Queue utilization of the server in proactive under various network conditions and NSI update frequency
4.3 主动分布式(PD)
PD除了以下三个主要区别之外与PC类似.
1)它是纯粹分布式的.没有服务器,每个节点都必须解决自身的优化问题.
2)每个节点只解决方程(4)中的分布式问题,而不是解决方程(2)中的中心问题.
3)集合N包含距离最近的邻居节点而不是所有节点,即使总节点很大(>100),N也被限制为几十个节点.
4.4 反馈分布式(RD)
如果只有少数节点过载并且低频发生,定期传输NSI可能会浪费资源.而且节点定期传输NSI会导致无人机经常处于高功率状态[16].在该算法中,节点只在需要帮助时进行通信.寻求帮助的节点广播请求帮助信息(RFH)并等待邻居发送他们的NSI进行响应.如果相邻节点的平均CPU利用率小于设定的阈值,则必须响应.一旦寻求帮助的节点从其他节点接收到NSI,它就制定并解决方程(4).为了避免使用旧信息并及时更新邻节点的当前状况,可以设置一个计时器Tth.一旦超过设定时间,节点必须广播RFH重新开始.该算法具体表述如下:
算法1.反馈分布式
1.ifγi+γi0≤μi//到达率小于计算能力
2. Setdvito not offload //无需卸载
3.else
4.ifRFH broadcasted & decision time 5. Follow previousdvi 6.else 7. Broadcast RFH to all nodes 8. Wait Twaitseconds for NSI 9.ifNo of NSI received≥2 10. solve Eqn.(4)for newdviand follow it 11.else 12. Broadcast RFH again,follow previousdvi 13. end if 14. end if 15. end if 在各调度算法运行时需要频繁解决方程(2)和方程(4)中所述的优化问题,该问题可以使用高效的线性编程技术来解决.目前解决线性问题的算法很多,所以在进行仿真实验比较各调度算法前先测试各线性规划算法的时间复杂度,以确定选用哪种线性规划算法. 对偶单纯形和内点算法是解决线性问题的常用方法.内点算法被认为是较有效,且占用内存少的算法.在不同数量的节点下进行实验来测量各算法的时间复杂度,发现内点是效果最好的(见图5),所以最终选定内点算法解决方程(2)和方程(4)中的优化问题.该实验是在台式机上使用英特尔E5-2630处理器,并在Linux环境下运行MATLAB 2013a进行的.这些算法在无人机上的运行时间可能会更长,但应该遵循相似的规律. 使用上文中设计的模拟器进行均衡调度算法的比较实验,该模拟器可以适应无人机类三维移动目标.模拟器模拟放置在3×3网格上的九个如图1所示的无人机,无人机间通过Wi-Fi相互连接,Wi-Fi设置为10 Mbps.每架无人机可以检测穿过其视场角的目标.为便于实验,假设所有节点的资源信息(剩余能量,实时CPU负载等)可用,并且所有无人机具有相同的初始计算能力.在模拟开始时,电池电量均匀分布在0-10瓦时之间.公式(10)中r的均值从0-1(满载)均匀分布,标准偏差固定为0.1.测试设备的CPU参数见表1.这些参数在仿真过程中不会改变.对于任务模拟,本文使用随机路点模型(RWP)[19].在RWP中,目标在三维空间随机位置产生.目标 表1 CPU参数 Frequency245.0384.0460.8499.2576.0614.4652.8691.2768.0806.4844.8998.4βcpufreq201.0257.2286.0303.7332.7356.3378.4400.3443.4470.7493.1559.5βcpuidle35.139.535.236.539.538.536.739.640.238.443.545.6 可能暂停一段时间,也可能移动到下一个目的地.当它选择下一个目的地时,它会以随机但恒定的速度向它移动;该过程重复,直到它移出平台.RWP的非均匀空间现象意味着目标集中在平台的中间[19],可以使用这种现象和不规则的视场角来模拟九架无人机间的不规则负载.位于平台中间的无人机可检测到目标数量最多. 图5 各线性规划算法的时间复杂度Fig.5 Time complexity of various linear problem solvers 实验运行100次蒙特卡洛模拟,每次运行代表20分钟的仿真时间.实验过程中目标产卵率高于死亡率,因此所有节点的任务到达率通常会随时间增加(见图6).每隔一分钟拍下任务完成情况和能量消耗的快照,并将其作为任务到达率γ的函数进行绘制(见图7).结果符合预期,Oracle的结果最理想,NC表现最差.PC的结果次好,但也消耗更多能量.在到达率上升到总标准到达率的约60%之前,RD和PD的性能优于PC,明显优于非协作情况.并且RD的功耗仅略高于PC,PD在该点附近甚至低于PC.但是随着目标到达率的升高,分布式算法的性能明显降低.此外,图7(b)显示了RD在更高的目标到达率下的较低功耗,但这也与其性能的下降一致.这是因为随着目标到达率升高,越来越多的邻节点更加忙碌.实验表明分布式算法适合较低的任务到达率,而集中式算法适合较高的任务到达率. 图6 仿真时间内每个节点的任务到达率Fig.6 Task arrival rate per nodes over simulation time 图7 仿真过程中的任务处理与能耗情况Fig.7 Task processing and energy consumption in the simulation process 实验中将处理得分定义为在分配时间内成功执行的任务与到达任务的百分比,并将其作为能量消耗的函数进行绘制(见图8).效能得分定义为成功执行量与消耗能量的比率,结果见表2.综合比较表2和图8发现,图8中性能和能耗几乎成线性关系,这意味着在必要的时候可以通过增加额外的能耗来提高性能,只要所有节点的任务到达率小于无人机网络的总计算能力,就可以考虑通过增加一定的能耗来换取性能和效率上的收益. 表2 仿真结果(平均超过100次) 算法到达率/分钟服务率/分钟能量消耗(J)处理得分效能得分(/100J)NCOPCPDRD6.916.916.916.916.914.346.105.844.845.3499510611055100910430.630.880.850.700.770.440.570.550.480.51 图8 所提算法的处理得分Fig.8 Process score of proposed algorithms 本文使用Open Jackson网络将多无人机边缘自组网络建模为队列网络.提出了多种主动式和反馈式协作算法,与非协作的无卸载式方案相比,显著提高了无人机编队野外作业系统的性能.结果符合预期,即如果总任务到达率小于总计算能力,并且其他节点的NSI可用,系统就可以不依赖云端在边缘完成所有任务.反馈分布式和主动集中式分别适用于不同的外部任务到达率,在未来的工作中,我们计划制定一个混合策略,可以根据任务到达率在它们之间切换.并且在真实的动态场景上应用该方案.5 实验比较与分析
5.1 计算复杂度测试
5.2 仿真实验设置
Table 1 CPU parameters
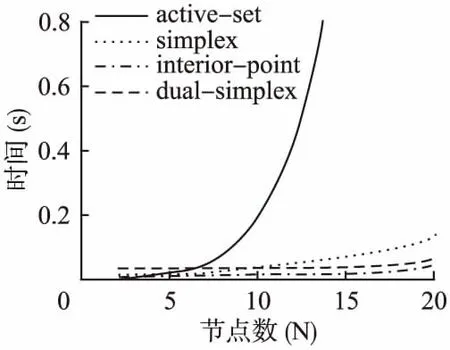
5.3 仿真实验结果与分析
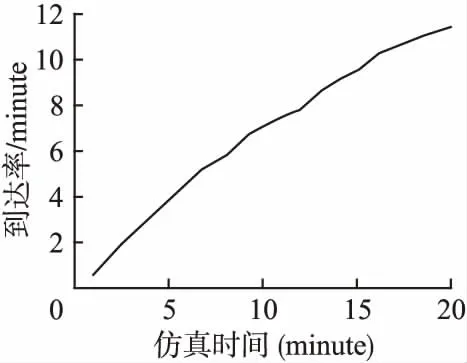

Table 2 Simulation results(averaged over 100 runs)

6 结 论

