低频振动模态参数辨识方法与预警指标研究

宁 星，任 伟，刘 君，田 黎

（1.长沙理工大学电气与信息工程学院，湖南 长沙 410114；2.国网湖南省电力有限公司检修公司，湖南 长沙 410004；3.国网湖南省电力有限公司水电分公司，湖南 长沙 410000；4.国网重庆市合川区供电公司，重庆 404100）

0 引言

近年来，我国电力工业规模不断扩大，已发展为区域互联电网。互联电网能有效地提高输电运行效率，但多区域之间的弱互联有可能引发低频振荡［1］。国内外一些典型事故亦表明，若不能有效抑制低频振荡，电力系统稳定运行将遭到破坏［2-4］。然而，振荡过程复杂多样，且夹杂着各种各样的外部噪声，导致振荡信号出现较强的非线性和非平稳性。因此，对含噪声、非平稳、时变的振荡信号进行分析，快速准确地获取振荡模式特征以满足实时在线分析与预警的要求，是大区域电网有效控制及安全运行的关键［2］。随着高速通信系统的快速发展，基于相量测量单元（Phasor Measurement Unit，PMU）的电力系统广域测量系统 （Wide Area Measurement System ，WAMS）为低频振荡动态特性分析与预警提供了新的契机［3］。

目前，基于WAMS的低频振荡监测分析主要用于振荡事件发生后的告警分析，并未充分发挥其预警作用。对低频振荡现象进行安全预警，为调度运行人员提供可靠的预警指标，是非常迫切的课题［4］。当前基于WAMS测量信号的低频振荡分析方法主要有：小波分析法、Prony算法、Kalman滤波法、HHT分析法、原子分解法、ESPRIT法等［5］。小波分析法具有多分辨率分析的特点，但在小波基的选取和结果精度方面还有待改进［6］。Prony法是目前比较流行的分析方法，已应用于各大电网公司，但Prony算法在噪声抑制、阶数辨识以及非平稳信号的拟合等方面效果不是很理想［7］。Kalman 滤波法［8］是一种用于系统辨识的递归运算法，该方法最主要的问题是数值不稳定，鲁棒性待提高。HHT算法［9］能够有效地处理非平稳信号，而模态混叠、边界分量等问题对算法的准确性有较大的影响。原子分解法［10］的时频跟踪能力较强，适用于非平稳时变信号的分析，其算法本质上需要进行大量的内积运算，辨识精度低。TLS-ESPRIT法是一类基于子空间技术的信号参数辨识法，该方法对高斯白噪声有较好的免疫能力，但其需要对采样信号进行两次奇异值分解，计算速度较慢，另外，该方法基于单通道信号，使得辨识精度不高，同时对非线性信号的分析有一定的限制［11］。

针对上述方法的不足，将用于分析航空航天、机械结构振动特性的多通道特征系统实现算法（Eigensystem Realization Algorithm，ERA）［12-13］与随机减量技术（Random Decrement Technique，RDT）相结合，应用于环境激励下低频振荡信号模态辨识与预警，提取其阻尼比、频率和振荡模态等参数，并及时、准确地反应系统的当前动态特性。该方法具有较强的抗噪声能力以及出色的并行能力，可用于广域多通道量测信号的实时在线分析与预警。

1 随机减量技术原理

随机减量技术（RDT）是一种从环境激励下系统的随机响应信号提取自由振荡信号的有效方法［14-15］，由H.A.cole等人在20世纪60年代末提出，已成功地应用于分析航天器在环境激励下的动态响应特征。

在电力系统中，当发电机采取经典二阶模型时，系统运行点处进行线性化，可得：

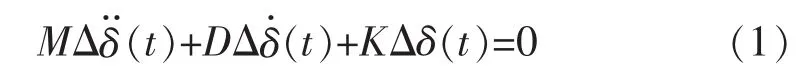
式中：Δδ为发电机转子角增量；M、D、K分别为发电机惯性时间常数、定常阻尼系数和同步力矩系数。

用F（t）表示负荷波动激励。若电力系统中所有的发电机同时运行，则：

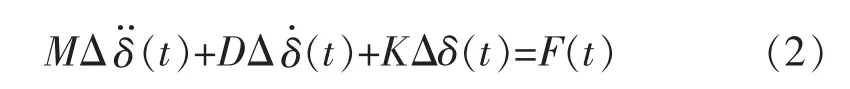
先选取触发时刻ti，并在每个ti后均取长度为L的响应信号，方程（2）满足：

式中：τ=1，2，…，L。

对于随机响应信号，提取N段具有长度相同的响应，再求得其平均值，可得：

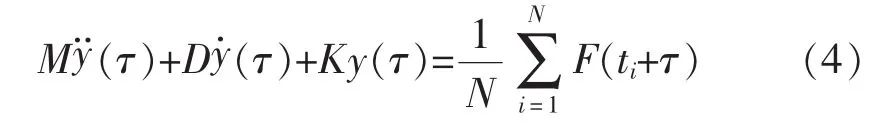
当电网处于稳定运行状态时，负荷激励服从高斯分布，即N→∞时，，方程（4）变为

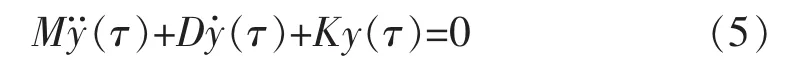
因此，对于方程（2）所描述的环境激励下负荷的随机波动方程，可转化为方程（5）描述的自由振荡响应方程，通过对方程（2）中的非齐次解 Δδ（t）的多次平均求得方程（5）的齐次解 y（τ）。y（τ）即为所求的自由振荡响应信号。

ti（i=1，2，···，N）称为触发时刻，由触发条件确定。只有选择合适的触发条件，才能准确提取系统随机响应中的自由振荡信号。本文选用工程领域应用最多的水平穿越触发条件，可得：

对于离散化的线性系统，当ti满足式（7）时，可认定为触发时刻。

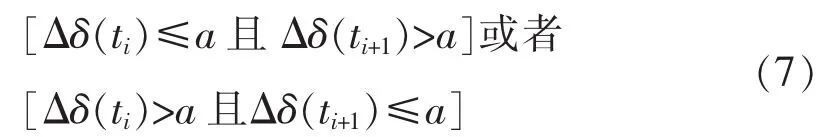
2 基于RDT-ERA方法的振荡模态分析

2.1 ERA方法原理

ERA法是近年来出现一种多输入多输出（Multiple Input Multiple Output，MIMO）的模态参数辩识方法，最早由NASA所属的Langley研究中心提出，被广泛用于航空航天领域，分析航天器的振动特性［16］

电力系统是一个超大规模的非线性系统，在探讨小信号稳定性时，通常将其转化为线性时不变系统来处理。对于N维线性电力系统，设有m个输入U（k）和 n 个输出 Y（k），U（k）为通过 RDT 提取的自由振荡信号，则离散时间状态方程为

其中：X（k）为状态增量向量；状态矩阵A、控制矩阵B和观测矩阵C共同构成了系统的一个最小实现。则电力系统的响应数据可以表示为

构造Hankel矩阵：

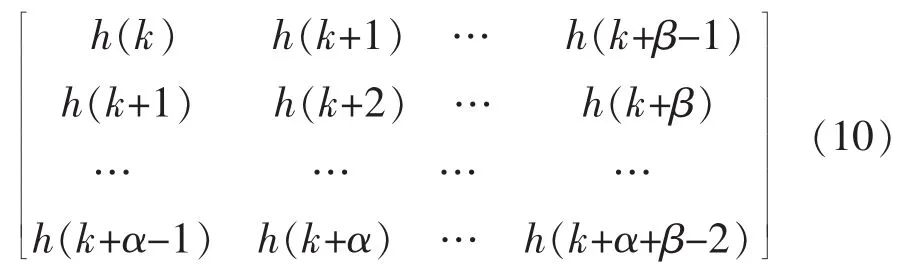
整理后有：

其中：α、β为任意整数；P和Q分别为广义的观测和控制矩阵。

在式（11）中，令 k=1，对 H（0）进行 SVD 分解可得：

其中U，V分别为左右奇异值向量矩阵，Σ为对角阵，即：

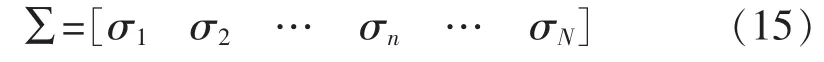
其中：σ1，σ2，…，σn，…，σN均为 H（0）的奇异值。

从式（15）可以看出，数值相对较小的奇异值σ对应于噪声模态或数值计算误差，因此，定义一个阈值ε，当第1个奇异值与第i个奇异值满足式（16）时，第i个及其后面的奇异值都可被舍弃，从而提高了辨识参数的抗噪性。

由式（14）可得：

设系统矩阵A的特征值矩阵为Λ，由指数矩阵的性质可得A1的特征矢量与A的相同，A1的特征矢量矩阵为

由此A的特征值矩阵 Λ=diag（λ1λ2… λ2n），且。

则对应于特征值λi的振荡频率fi和阻尼比ξi分别为

2.2 阶数确定

对于实际电力系统而言，系统的阶次是不确定的，因此在应用ERA算法前要对系统的阶次p进行确定［17］。

合理的阶次确定对系统模态辨识非常重要，目前用于ERA算法定阶的方法主要有奇异值跳跃法和稳定图法。奇异值跳跃法就是通过找出奇异值跳跃的点来确定模型的阶次，但奇异值按照从小到大排序时无明显突变，则无法进行判断。稳定图法需要计算系统处于不同阶次时的模态参数，计算量大，对计算机的要求较高［18］。

通过对式（10）所示的Hankel矩阵进行SVD分解来确定系统的阶次p。即定义模型阶次指标为

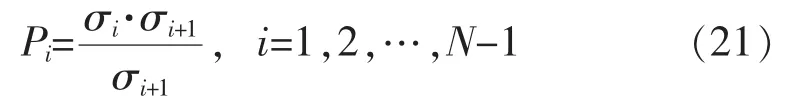
由于通过计算得到的奇异值 σ1，σ2，…σn…σN是按降序排列的正数，突降比较大的奇异值σi对应的pi也是一个大值。因此，将系统阶次p设定为模型阶次指标pi所对应的最大值。

3 算例仿真

3.1 数值信号算例分析

数值信号算例是含白色噪声的多通道低频振荡信号，构造复合信号 x（t）为

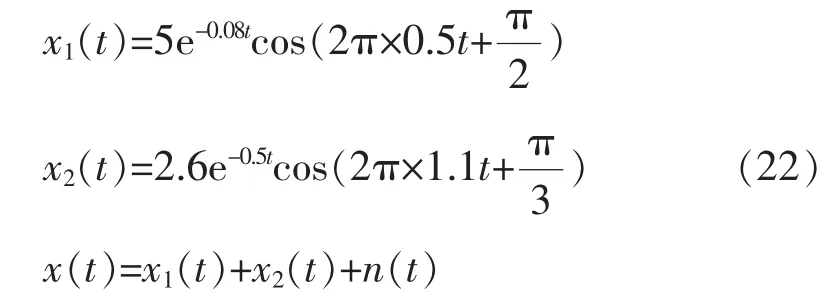
式中：n（t）为信噪比20 dB的高斯白噪声。为验证本文方法的有效性，分别采用RDT-ERA算法和传统的Prony算法对复合信号x（t）进行去噪与辨识，其去噪拟合结果如图1～2所示。为避免辨识结果出现偶然误差，将仿真进行100次，其辨识结果如表1所示。

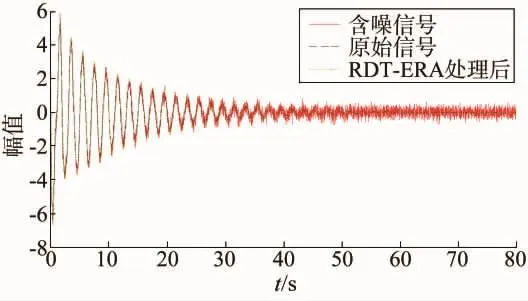
图1 RDT-ERA法辨识结果

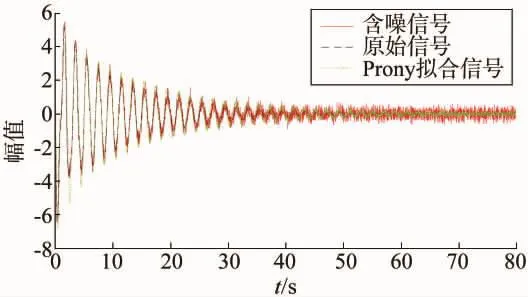
图2 Prony法辨识结果

由图1可知，对含有高斯白噪声的多通道信号直接使用Prony辨识，得到的拟合曲线与原始信号偏差较大且不能完全去除噪声，而基于RDT-ERA算法拟合效果更佳，基本上与原始信号重叠。表1给出了两种方法辨识结果的相对误差，由表可知基于多通道信号的Prony算法参数辨识精确度低，误差较大。而RDT-ERA算法辨识的参数相对比较接近理论值，相对误差均小于3%，由此可知本文方法在抗噪声和多通道信号模式参数辨识上具有一定的优越性。

表1 两种方法辨识结果比较

3.2 2区域4机系统分析

为了进一步验证本文方法的准确性和优越性，选择如图3所示的IEEE四机两区域系统为电力系统仿真算例［19］。在该系统中，发电机G1～G4都安装了励磁器、调速器和电力系统稳定器（PSS），两区域联络弱，负荷重，是非常典型的低频振荡模型。设定系统扰动为0.1 s时刻母线7和8之间的输电线路发生单相接地短路故障，故障点距离母线7的距离占整个线路的5%，0.15 s切除故障。利用PSASP软件的暂态稳定计算进行分析，输出每台发电机的功角曲线如图4所示。

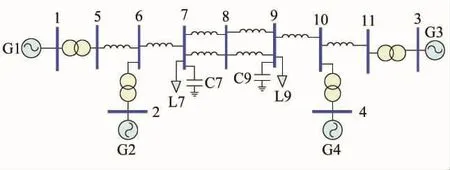
图3 2区域4机系统

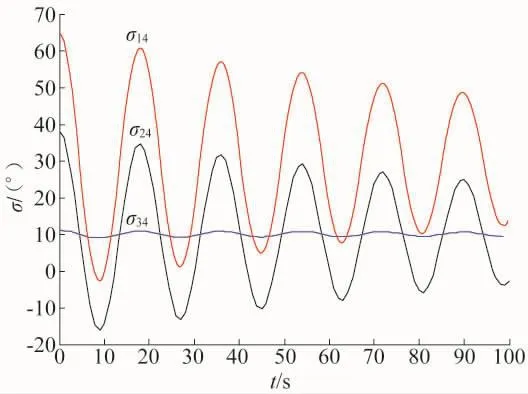
图4 各发电机功角曲线

对系统模型进行分析可得，该系统中存在3个低频振荡模式，其频率f和阻尼比ξ如表1所示。其中一个为区域型振荡模式，两个为局部振荡模式。振荡模式1为发电机G1和G2相对于发电机G3和G4振荡；振荡模式2为发电机G3和G4相互振荡；振荡模式3为发电机G1和G2相互振荡。相对于局部振荡模式，区域型振荡模式包含的发电机较多，其ξ也小很多，所以系统更容易趋向不稳定。

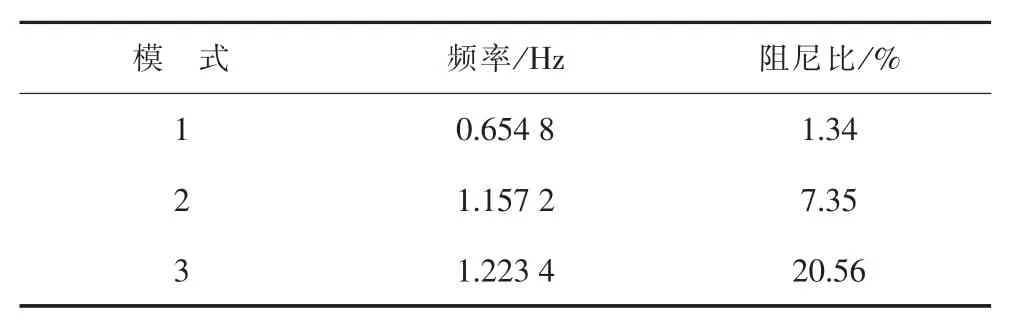
表2 4机系统低频振荡模式理论值

在PMU测量的数据中，经常带有噪声信号，为了检验本文方法在多通道下的抗噪性能，在对响应信号进行分析前，首先要排除环境的随机因素的影响，采用Monte Carlo Method思路，进行100次试验仿真，从而避免了环境激励的随机性对辨识结果产生误差。以重点关注的弱阻尼模式1作为例子来验证其抗噪性，将上述4台发电机的转速信号作为参考信号，自由振荡信号时间长度设为10 s，仿真时长为10 min。对输入的信号叠加不同分贝的高斯白噪声，采用ESPRIT法和本文方法分别进行辨识，辨识结果如表3所示。

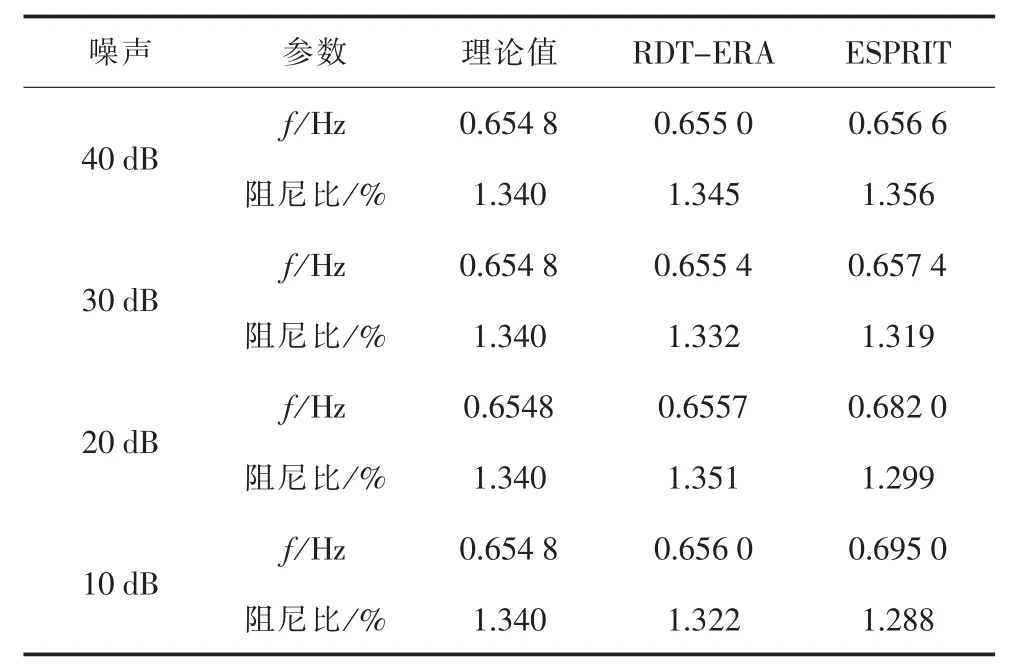
表3 两种方法在不同噪声下对弱阻尼模式

由表3可以看出，对含有不同高斯白噪声的信号，RDT-ERA算法能更准确地辨识低频振荡的模态参数，且相对于理想扰动的误差较小。而ESPRIT算法辨识的频率、阻尼比相对于理论值的误差较大，特别是随着量测噪声水平的提高，其变化越明显，表明本文方法具有较强的鲁棒性。另外，ESPRIT法是基于单通道信号的方法，需对4个机组输出信号进行逐一辨识，但RDT-ERA能同时对多组输出信号进行辨识，因此RDT-ERA在计算速度上具有一定的优势。同理，以相同的方法辨识模式2和3，结论依然成立。

图5和图6表示在量测噪声水平为20 dB时，使用RDT-ERA方法以及ESPRIT法进行辨识的拟合曲线。从拟合曲线可以看出，对于含有量测噪声的信号，ESPRIT算法拟合的曲线有较大的偏差，而基于RDT-ERA算法的拟合曲线在总体趋势上更加吻合。

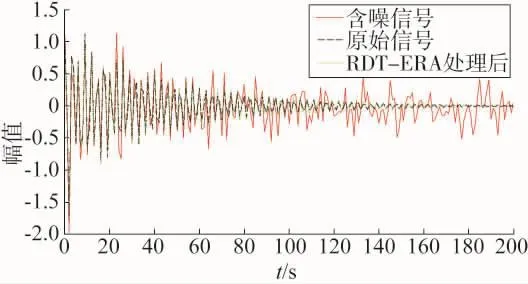
图5 本文方法拟合结果

图6 ESPRIT算法拟合结果

3.3 主导模式最弱阻尼比指标预警

主导模式最弱阻尼比指标一般与电力系统的网架结构特征值有关，因此本文从电力系统的网络结构本质特性对其进行预警分析。根据主导模式最弱阻尼比指标，将低频振荡分为3个等级：当阻尼比大于3%时系统阻尼较强，此时系统较难出现低频振荡现象，安全等级较高；当阻尼比处于0～3%时可认为系统阻尼较弱，此时系统有可能发生低频振荡问题，安全等级较弱；当阻尼比小于0时，系统将会发生增幅性振荡，电力系统处于高度危险状态，需采取对应策略进行抑制。指标等级评价如表4所示。

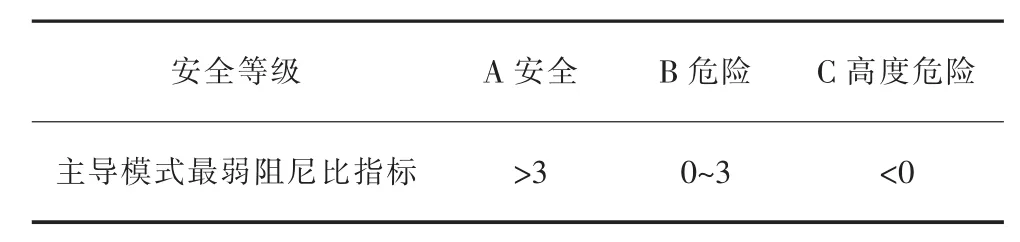
表4 主导模式最弱阻尼比指标等级评价 %

由仿真辨识得到的主导模式阻尼比在阈值3%之下，此时系统发出报警，系统运行人员应及时采取有效措施抑制其振荡。

4 结语

针对电力系统由负荷的随机波动引起的响应信号进行低频振荡辨识与预警，提出了将随机减量技术（RDT）和特征系统实现算法（ERA）方法相结合。在采用RDT从随机响应信号中提取系统自由振荡信号的基础上，使用ERA方法能够快速准确地识别低频振荡模式，得到其频率、阻尼比等参数。仿真分析表明，RDT-ERA法比Prony法、ESPRIT法的辨识结果更精确，抗噪声能力更强。同时，RDT-ERA法可以基于多通道信号，可一次性准确的辨识出多种振荡模式的结果，在计算速度和精度上表现更出色。

该方法仅讨论高斯白噪声环境激励下的在线辨识与预警，具有良好的准确性和有效性，使该方法的适用范围存在有限性。课题下一步将研究在高斯有色噪声的信号下，解决在线监测、预警等方面的问题，扩大其应用范围。