广义核-卫星图的无符号拉普拉斯谱*

田贵贤, 孙 眉

(浙江师范大学 数学与计算机科学学院,浙江 金华 321004)

0 引 言

图的谱不仅能很好地反映图的结构(如简单图恰有一个正特征值当且仅当它是一个完全多部图；若图的代数连通度大于0,则其必连通[1-2]等),而且图的谱也可以用来研究图的其他性质，如图的能量[1]、生成树的数量[2-3]、(度)基尔霍夫指数[4-5]、整谱图的构造[6-7]等等.

本文主要研究核-卫星图和广义核-卫星图的无符号拉普拉斯谱.

设G=(V,E)是一个有n个顶点、m条边的无向连通简单图，其中顶点集为V，边集为E.用di表示顶点vi的度，即与顶点vi相关联的边的条数.图G的邻接矩阵A(G)=(aij)n×n是一个n阶方阵，其元素满足：若vi和vj相邻，则aij=1；否则，aij=0.矩阵A(G)的所有特征值的集合称为G的谱.用D(G)=diag(d1,d2,…,dn)表示图G的度对角矩阵,称L(G)=D(G)-A(G)为图的拉普拉斯矩阵;称矩阵L(G)的所有特征值的集合为G的拉普拉斯谱;称Q(G)=D(G)+A(G)为图G的无符号拉普拉斯矩阵;称矩阵Q(G)的所有特征值的集合为G的无符号拉普拉斯谱.

设G1=(V1,E1)，G2=(V2,E2)是2个简单图.若图G1∪G2=(V,E)的点集为V=V1∪V2,边集为E=E1∪E2，则称G1∪G2是G1与G2的并.若图G1G2=(V,E)的点集与边集分别为V=V1∪V2和E={eij|∀vi∈V1,vj∈V2}∪E1∪E2，则称G1G2是G1与G2的连图.为简单起见，η个G的并，记为ηG.

定义1[8]设c≥1，s≥1，η≥2.称图Θ(c,s,η)≅Kc(ηKs)为以Kc为核团、以η个Ks为星团的核-卫星图，其中Kc表示c个点的完全图.

由于在现实世界的复杂网络模型中，并非所有的星团都相同.因此，需要进一步考虑将核-卫星图推广到具有多个不同星团的情形.

定义2[8]设si≥1,ηi≥1,i=1,2,…,t.称图Θ(c,s,η)≅Kc(η1Ks1∪η2Ks2∪…∪ηtKst)为广义核-卫星图，其中s=(s1,s2,…,st),η=(η1,η2,…,ηt).

显然，核-卫星图Θ(c,s,η)是广义核-卫星图Θ(c,s,η)的特殊情形，即t=1时的情形.

近些年，运算图的各类谱得到广泛研究，如Indual[6]引入了细分点、细分边连图的概念并刻画了它们的邻接谱与因子图的邻接谱之间的关系,也构造了一些整谱图；文献[4]进一步刻画了细分点、细分边连图的邻接谱，拉普拉斯谱，以及无号拉普拉斯谱与因子图的相应谱之间的关系，也构造了一些同谱图对,并计算了上述图类生成数的数目和基尔霍夫指数；文献[9]又将上述部分结果推广到更一般的情况，即将点连和边连的情况同时进行考虑，给出了双连图的概念.同时,也刻画了关于细分图、R-图、Q-图及全图的双连图的拉普拉斯谱.最近,文献[7,10]也刻画了几类特殊的连图的无符号拉普拉斯谱，进一步构造了一些无符号拉普拉斯整谱图.广义核-卫星图是区别于文献[4,6,9]中的连图变异类的一种特殊的连图,在现实世界的复杂网络模型中有着广泛的应用.Estrada等[8]研究了该图的聚类系数、度匹配系数,并通过构造特征值及对应的特征向量刻画这类图的邻接谱和拉普拉斯谱.

受上述研究的启发，本文将研究核-卫星图和广义核-卫星图的无符号拉普拉斯谱.通过构造核-卫星图和广义核-卫星图的特征值及对应的特征向量，得到它们的无符号拉普拉斯谱与核团、星团的结构关系.作为应用,本文也构造了一些无符号拉普拉斯整谱图，推广了文献[7，10]的部分相关结果.

1 广义核-卫星图的无符号拉普拉斯谱

给定广义核-卫星图Θ(c,s,η)，定义c×(ηisi)阶矩阵

和(ηisi)×(ηisi)阶准对角矩阵

其中:对角块上共有ηi个A(Ksi);i=1,2,…,t.

适当排列广义核-卫星图Θ(c,s,η)点的次序可以将其邻接矩阵表示成如下的分块形式：

Q=A+D=

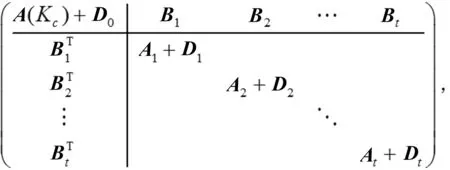
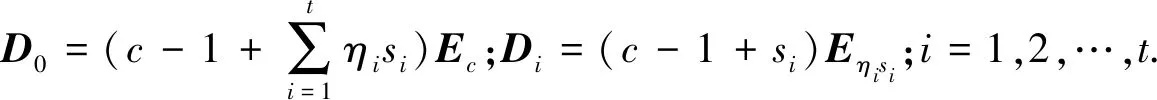
定理1广义核-卫星图Θ(c,s,η)的无符号拉普拉斯谱由下列特征值构成：

2)特征值λ=si+c-2，其重数为ηi(si-1)；

3)特征值λ=2si+c-2，其重数为ηi-1；

4)余下特征值是下列方程的根：

证明 注意到完全图Kc的谱为{c-1(1),-1(c-1)}，其中a(b)表示a重复b次.显然，1c是属于特征值c-1的特征向量.假设x1是属于特征值-1的特征向量,令向量

(1)

其分块方法与Q相同.那么特征方程Qx=λx等价于

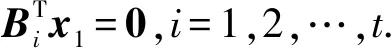
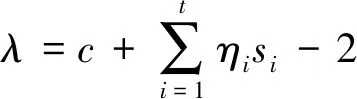
令向量

(2)

其分块方法与Q相同.那么特征方程Qx=λx等价于

λ=-1+(si-1+c).

由于Kc属于特征值-1的线性无关的特征向量有si-1个,而同一类星团的个数为ηi,故特征值λ=si+c-2的重数为ηi(si-1).

令非零向量

其中,x中的非零块出现在对应于Q中的对角线块Ai+Di的位置上，且分块方法与Q相同.因此，由特征方程Qx=λx可得

其中,Di1=Di2=…=Diηi=(c-1+si)Esi.从而上式等价于(A(Ksi)+Dij)1si=λ1si,j=1,2,…,ηi.故

λ=si-1+(si-1+c).

再由方程α1+α2+…+αηi=0的解空间的维数是ηi-1可得λ=2si+c-2的重数为ηi-1.

最后,分2种情况讨论余下的t+1个特征值 .当t=1时,该图为核-卫星图Θ(c,s1,η1).令向量

其分块方法与Q相同.由特征方程Qx=λx可得

上式表明:

2(c-1)+η1s1+βη1s1=λ;

c+β(2(s1-1)+c)=λβ.

消去β可得

进而有

λ2-(η1s1+3c+2s1-4)λ+

(η1s1+2c-2)(c+2s1-2)-cs1η1=0.

解此二次方程可得

下面假设t>1，令向量

其分块方法与Q相同.显然,这种形式的向量与式(1)和式(2)中的所有特征向量都正交.对于这样的向量，由Qx=λx可得

所以

(3)

c+βi(2si-2+c)=λβi.

(4)

整理可得,

所以

该方程决定了广义核-卫星图Θ(c,s,η)的剩余t+1个特征值.定理1证毕.

例1设广义核-卫星图Θ(c,s,η)=Θ(2,23,15)如图1所示.

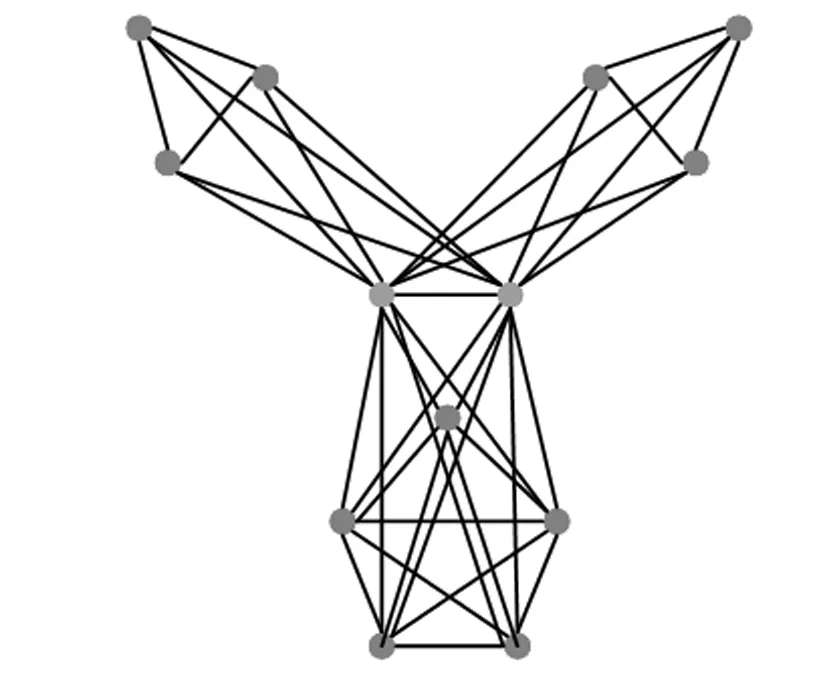
图1 广义核-卫星图Θ(2,23,15)

由定理1可得其无符号拉普拉斯谱特征值为：

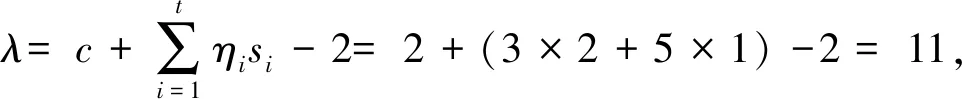
2)λ=s1+c-2=3,其重数为η1(s1-1)=4,λ=s2+c-2=5,其重数为η2(s2-1)=4;

3)λ=2s1+c-2=6,其重数为η1-1=1;

λ3-29λ2+246λ-600=0⟹

λ1=15.905 0,λ2=8.815 9,λ3=4.279 1.

通过Matlab直接计算，可得Θ(2,23,15)的无符号拉普拉斯谱为{11,3(4),5(4),6,15.905 0,8.815 9,4.279 1}，进一步验证定理1成立.

在定理1中令t=1,可得核-卫星图Θ(c,s,η)的无符号拉普拉斯谱.

定理2核-卫星图Θ(c,s,η)的无符号拉普拉斯谱由下列特征值构成：

1)特征值λ=c+ηs-2，其重数为c-1；

2)特征值λ=s+c-2，其重数为η(s-1)；

3)特征值λ=2(s-1)+c，其重数为η-1；

4)余下2个特征值为

例2设核-卫星图Θ(2,2,3)如图2所示.

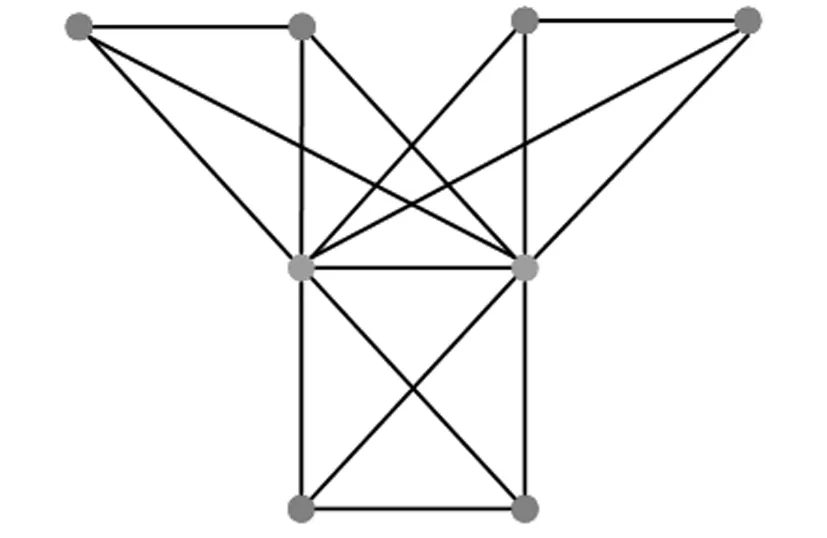
图2 核-卫星图Θ(2,2,3)

由定理2可得其无符号拉普拉斯特征值为：

1)λ=c-2+ηs=6,其重数为c-1=1;

2)λ=s+c-2=2,其重数为η(s-1)=3(2-1)=3;

3)λ=2(s-1)+c=2(2-1)+2=4,其重数为η-1=3-1=2;

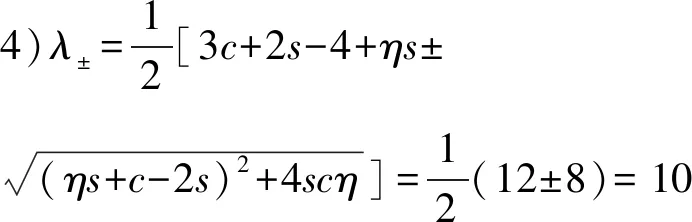
用Matlab直接计算可得Θ(2,2,3)的无符号拉普拉斯谱为{2(4),4(2),6,10}，进一步验证定理2成立.

在定理2中,若令c=m,s=1,η=n,则

m(n-1); (n+m-2)(m-2).

其中，a(b)表示a重复b次.

众所周知，整谱图的构造是图谱理论研究的重要课题，文献[7]研究了正则图的连图的无符号拉普拉斯谱，并构造了一些无符号拉普拉斯整谱图.直接利用定理2,可得核-卫星图Θ(c,s,η)是无符号拉普拉斯整谱图的充分必要条件,该结果推广了文献[7]中的主要结果.

定理3核-卫星图Θ(c,s,η)是无符号拉普拉斯整谱图的充分必要条件是

(ηs+c-2s)2+4scη∈Z2.

证明 定理2表明核-卫星图Θ(c,s,η)是无符号拉普拉斯整谱图当且仅当

是整数.由于ηs+3c+2s-4与(ηs+c-2s)2+4csη有相同的奇偶性,故λ±是整数当且仅当

(ηs+c-2s)2+4scη∈Z2.

定理3证毕.

直接应用定理3,可得:

在定理1中,若令t=2,η1=η2=1,即广义核-卫星图仅含有2个不同的星团，则

推论3[7]广义核-卫星图Θ(c,s,η)≅Kc(Ks1∪Ks2)是无符号拉普拉斯整谱图的充分必要条件是(c+2s1+2s2)2-16s1s2∈Z2.

证明 由定理1知,Kc(Ks1∪Ks2)是无符号拉普拉斯整谱图当且仅当三次方程

(λ-2c-s1-s2+2)(λ-2s1-c+2)×

(λ-2s2-c+2)=

c(s1(λ-2s2-c+2)+s2(λ-2s1-c+2))

的根是整数.根据三次方程的求根公式,类似于定理3的证明可得结论成立.推论3证毕.

推论4[7]对于n∈Z+,1≤j<2n，图Kj(K2n-j∪Kn)是无符号拉普拉斯整谱图.特别地，图Kn(Kn+2∪Kn+1),Kn+2(Kn∪Kn+1),K1(K2n-1∪Kn)和K2n-1(K1∪Kn)也都是无符号拉普拉斯整谱图.

2 结 语

本文刻画了广义核-卫星图的无符号拉普拉斯谱,应用所得结果给出了几类图是无符号拉普拉斯整谱图的充要条件.由于广义核-卫星图是一种特殊的连图,因此本文结果进一步表明,图的运算(如连运算、冠运算、积运算等)是构造无符号拉普拉斯整谱图的有效方法.另外, 广义核-卫星图是现实世界的复杂网络模型之一,有着广泛的应用背景.显然, 对于复杂网络中的其他模型,也可以考虑刻画其无符号拉普拉斯谱及相关问题.