基于20 L球罐的多相混合物扩散模拟*

张成均, 白春华

(北京理工大学 爆炸科学与技术国家重点实验室，北京 100081)

0 引言

近几年，由于工业生产导致的粉尘爆炸事故和军用FAE武器(燃料空气炸弹)对可燃粉尘利用率的增加，科研人员对于粉尘爆炸的研究不断深入。以气固两相混合物为背景的研究较为广泛并趋于完善，以气液固三相混合物为背景的研究越来越受重视，但是由于三相混合物爆炸的机理更为复杂多变，目前对三相混合物爆炸的理论还不完善。针对粉尘爆炸的研究主要集中在爆炸机理和爆炸特性参数等方面[1]，分实验和模拟2部分。爆炸下限是粉尘爆炸的重要属性之一，合适的点火延迟时间对确定其爆炸下限具有重要意义。研究点火延迟时间关系到粉尘的分散状态。传统意义上，点火延迟时间通常是认为从喷粉到点火经历的时间段，主要依据气相湍流度达到最大[2]。点火延迟时间要避开湍流强度由零值到最大值的阶段，所以一般实验研究中，最小点火延迟时间通常大于50 ms。在粉尘等容燃烧实验研究中，为减少扬尘湍流强度对粉尘固有燃烧特性的影响，尽量使用对称结构的扬尘装置，且点火延迟时间应设置在100 ms以后[3]。国内外在爆炸领域对于点火延迟时间的研究，认为能产生最大爆炸压力的点火延迟时间为最佳点火延迟时间，进而用来定义不同粉尘的爆炸特性，如刘义、李润之等[4-5]在研究不同粉尘的爆炸特性时均以固定的点火延迟时间作为研究条件，具有一定的限制性；张博、Liu、刘龙等[6-8]通过实验验证了不同初始反应条件对应不同的最佳点火延迟时间；陈嘉琛、沈世磊、白建平、何琰儒等[9-12]利用数值模拟讨论验证得出点火延迟时间受粉尘粒径、云团属性和分散状态的影响；Sanchirico， Sarli等[13-14]利用Fluent建立三维模型研究了在标准20 L球的爆炸罐内铝粉浓度和湍流动能的变化情况。对于气液固三相混合物，液相的存在对于粉尘云团的分散过程具有重要影响。从安全生产的角度来看，对三相混合物的点火延迟时间不能使用粉尘爆炸默认的规律，所以探究三相混合物的分散规律，并讨论三相混合物点火延迟时间的确定范围具有很重要的学术和实际意义。

本研究以上述内容作为背景，选取燃料空气炸弹常用原料铝粉、乙醚和空气为研究对象，研究气固两相和气液固三相的混合物扩散演化规律，按照20 L球型罐体设计图建立三维非线性计算模型，利用FLUENT软件进行数值模拟，以实现罐体对罐体内铝粉浓度变化和流场湍流动能的实时监测。

1 计算模型及参数

1.1 计算模型

1.1.1 20 L球罐模型

本实验使用喷头对喷形式的20 L球型罐，包含二次脉冲气动喷雾多相爆炸测试系统，王悦[15]设计并进行了大量乙醚的云雾场燃爆参数实验研究，证明该设计具有良好的分散效果符合科研要求。20 L球罐爆炸系统如图1所示。

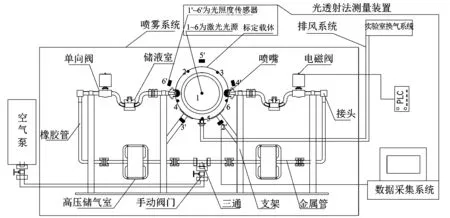
图1 20 L球罐爆炸系统Fig.1 20 L spherical explosion system

对爆炸系统设计图进行简化，建立三维模型。根据实验设备构成和Fluent模拟设置的性质，将实验系统简化为体积为20 L的球体和内嵌的1对喷头。喷头实际直径为40 mm，顶部中心点及邻近两圈的小孔孔径为1 mm，以外的孔径1.5 mm，如图2(b)所示。喷头定义为内部的Wall，小孔部分为球面上的孔洞，孔数共189个。喷头的面网格31 103个，最大尺寸0.000 5 m。简化模型面网格数106 793个，最大尺寸0.01 m。体网格数1 258 790个，最大尺寸0.5 m。如图2所示。

图2 简化后网格模型Fig.2 Simplified mesh model

1.1.2 离散相模型

铝粉颗粒粒径小，只考虑流体拽力和重力，其他一般忽略不计[16]。粉尘颗粒属性根据FLUENT中DPM非稳态离散相模型定义，在拉氏坐标系下积分颗粒作用力微分方程来求解离散相颗粒的轨道。颗粒的作用力平衡方程(颗粒惯性=作用在颗粒上的各种力)在笛卡尔坐标系下的形式(x方向)为:

(1)

式中：FD(u-up)为颗粒的单位质量曳力；u为流体相速度；up为颗粒速度；ρ为流体密度；ρp为颗粒密度(骨架密度)。

(2)

曳力系数CD可采用如下的表达式:

(3)

式中：μ为流体动力粘度；dp为颗粒直径，Re为相对雷诺数(颗粒雷诺数)。其定义为:

(4)

1.1.3 连续相模型

国内外对于气液固多相的数值模拟多为将液相雾化为小液滴，在本模型架构中，颗粒相速度初始值较大，经测试液滴与铝粉之间影响作用很小，且扩散速度远快于铝粉，与实际相差较大，不适合本模型介于计算机硬件条件限制，经反复试验得出1个方案：将液相部分作为罐体内初始连续相一部分，作为初始条件使之在颗粒相和空气相的动量交换作用下，在喷头中完成混合，在球罐中实现气液固三相之间的分散混合。

混和物模型的动量和质量方程，是通过相对速度来描述离散相，粒子运行轨迹的计算是独立的，它们被安排在流体相计算中指定的间隙内完成，其耦合作用是双向的。颗粒相的动量变化通过公式(5)求解连续相传递给离散相的动量值F，随后汇到流体相动量平衡计算中。同理，质量变化通过公式(6)求解连续相传递给离散相的质量值M，随后传给流体相质量平衡的计算中。

(5)

(6)

1.2 计算参数设置

本研究中颗粒相选用片状铝粉，总质量为5.4 g，密度为2 719 kg/m3，粒径为10 μm，形状系数φ=0.5(φ=s/S，其中s为与实际颗粒具有相同体积的球形颗粒的表面积，S为实际颗粒的表面积)。液相选乙醚，材料属性系统默认，空气相选择理想气体。使用SIMPLE算法，标准K-ε模型，标准壁面函数，Mixture多相流模型，考虑重力影响。

入口同时注入颗粒流和空气流，吹粉压力为0.4 MPa，作用时长为50 ms，50 ms后压力差终止，燃料做惯性运动。离散相在连续相中湍流流动，时间步长为0.001 ms，迭代时间步数为150步，每个时间步长迭代20次，先计算10次连续相后耦合10次颗粒相，双向耦合。假设压力差全部作用于铝粉，作用时长50 ms ，燃料在内径为8 mm的管道内视为加速阶段，加速长度x=0.3 m如图3所示，进入喷头视为进入开放空间没有加速效果，简化模型中留有长度为15 mm的管长以便预放液相部分。忽略阻力因素影响，利用式(7)～(9)计算得铝粉粒子在进入喷头时的平均速度为115 m/s。

(7)

对上式积分求解

(8)

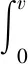
(9)

式中：p为吹粉压力，Pa；S为管道横截面面积，m2；v为吹粉时刻的速度，m/s；m为铝粉质量，kg/m3。

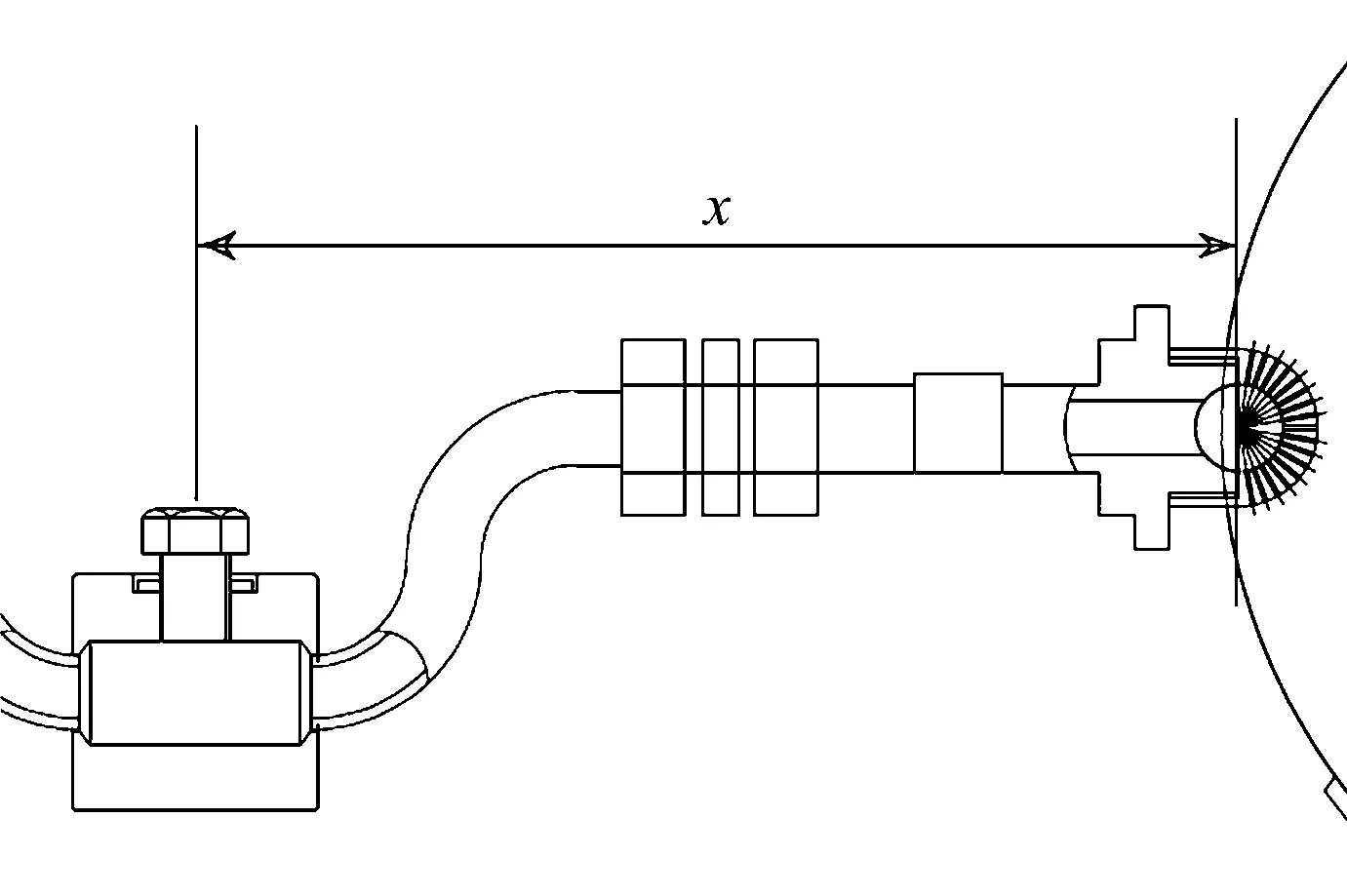
图3 加速区间xFig.3 The section of increase speed

2 计算结果及分析

不考虑粒径和粉尘浓度变化的影响，分别对气固两相和气液固三相的分散进行模拟，监测铝粉粒子分布情况、罐体截面湍流动能变化情况、液相分散情况、球心点火点铝粉浓度曲线图等等。

2.1 计算模型球罐中铝粉粒子浓度演化分布图

对比分析球罐内部气固两相和气液固三相湍流分散过程中相态参数的演化规律，截取10，30，50，100和150 ms这5个具有代表性的时间点，观察其基于铝粉浓度(kg·m-3)的粒子轨迹和中心截面处的湍流动能(k)变化云图，左侧色标从下往上表浓度量级递增，如图4所示。

本研究共150 ms，前50 ms为喷粉阶段，后100 ms为湍流混合阶段。在喷粉阶段两侧基本以中轴面对称，如图4(a)、(c)所示10 ms前后铝粉粒子呈云团状，粒子整体向球心方向移动，喷头处浓度高于粉尘云前段。

图4 铝粉浓度粒子分布A和湍流动能B变化过程Fig. 4 Particle tracks of concentration A and the change of turbulent kinetic energy B

图5 湍流场Fig.5 Turbulent flow field

在30 ms前后，由于喷头空间内形成的流场如图5(b)所示，铝粉粒子由喷头喷出，后向四周扩散，由于粒子间的碰撞和连续相的混合，在粉尘云团前段的粒子速度降低，在喷头中流场的作用下，粉尘云团朝壁面方向运动，球心方向浓度极少。在50 ms前后，两团粉尘云前沿相遇，由壁面碰撞沿着中心对称面向球心扩散，在球心处交汇。在50～150 ms是湍流混合的过程，20 L球罐体内部流场如图5(a)中箭头所示。在罐体内部存在一个体回流圈，混合物沿着回流圈在内部逐渐混合。由图4(b)、(d)也可以看出，湍流动能的分布跟回流圈一样，回流中心湍流动能小，其他地方要大。对比2种工况下的湍流动能，0～50 ms气动喷粉阶段，两者湍流动能分布基本相同，高能处都集中在喷头小孔处量级在300～500 m2/s2，进入罐体后由于空间大，湍流动能骤减。喷粉阶段结束后，量级骤降至0～2 m2/s2。由于液相与颗粒相的相互影响，三相粉尘云团内部流场的湍流动能略小于两相。Gore等[17]归纳了两相流中流体湍流的部分实验数据，指出小颗粒削弱流体湍流，大颗粒增强流体湍流。樊建人等[18]研究了三维气固两相混合层中颗粒和流体的双向耦合，认为颗粒促使流场湍动能增加。加入液相后，颗粒相占比减少，侧面削弱了流场的湍流强度，使流场内部更趋于稳定。由于壁面的阻力作用，罐体内部壁面处的浓度要大于内部空间，且回流使得粉尘云团的沉积现象可忽略。

2.2 液相体积分数云图

图6由左至右分别对应10，30，50，100和150 ms共5个特征时间点液相体积分数的云图，左侧色标从下到上代表百分数递增。喷头中液相在气固相的气动下，与粉尘云团混合，并跟随粉尘云进入罐体，由于液相动能来自气固相传递，绝大部分液相在粉尘云内部，与铝粉、空气之间相互影响并扩散，使粉尘云团的湍流动能相对减小，从而扩散速度小于气固两相，相对应粉尘云团浓度大于气固两相粉尘云团。

图6 液相体积分数演化规律Fig.6 The change of liquid volume fraction

2.3 点火点浓度变化曲线

监测球心点火点的铝粉浓度的变化，得到图7曲线。本研究铝粉共5.4 g，所以在罐体中的平均浓度为0.27 kg/m3，作为本实验来说该浓度为标准浓度。

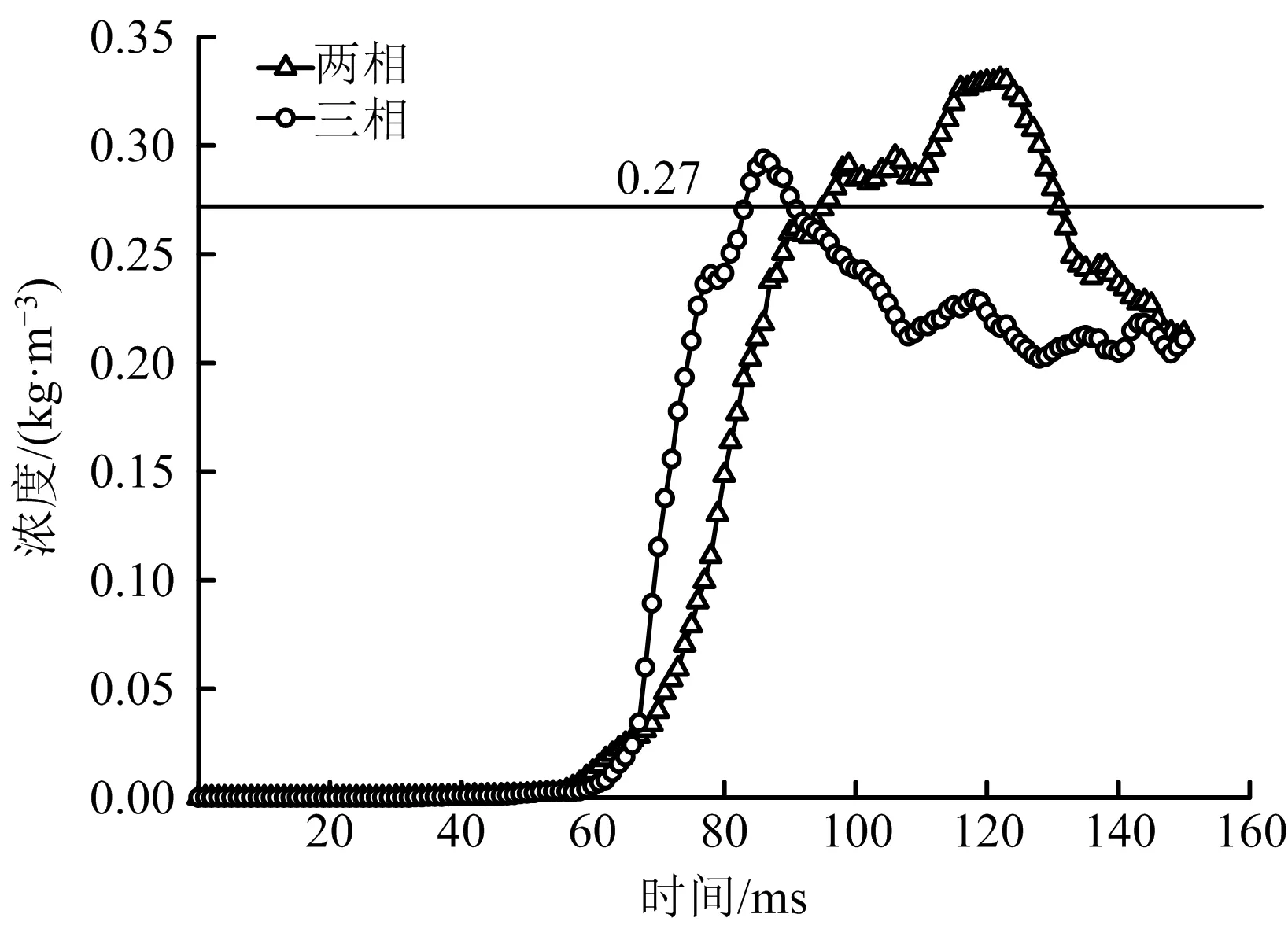
图7 点火点铝粉浓度变化曲线Fig.7 The change of aluminum concentration at ignition point

由图7球心点火点铝粉浓度的变化曲线可以看出，两相扩散浓度变化曲线的前60 ms浓度开始突增，说明粉尘云前段已经扩散到球心点，随后快速增加。而三相扩散浓度曲线可知，浓度突增要晚于两相，但是增长速度要快于两相，结合云图分析可知，由于液相的存在降低了整个流场的湍流强度，粉尘云前段扩散稍慢，但是粉尘云内部混合更充分，所以导致该点浓度出现晚增加快。

由曲线可知，三相混合物爆炸下限的点火延迟时间应该在80～90 ms，该段区间球心点的浓度高于标准浓度，实验得到的下限更安全。

对于两相而言，在95 ms处达到标准浓度，由于湍流动能高，高于标准浓度的点火浓度区间在90～130 ms，从实验结果的安全性和准确性考虑，对于气固两相混合物爆炸下限的点火延迟时间为90～100 ms，结论：三相混合物爆炸下限的点火延迟时间应该小于两相混合物。

2.4 实验验证结论

使用尺寸比例为1∶1的20 L透明罐系统对于分散实验进行验证，实验条件同模拟条件，使用高速摄影拍摄其分散过程。得到较为清晰的照片如图8所示。因为实验存在误差且随机性太强，操作过程中混合物混合不均匀等，很难达到数值模拟结果程度的对称性，会导致结果出现偏差。

对照图4(c)和图6中相应时间的模拟图分析，由图8中10 ms可以看出，粉尘云团主要分布在喷头周围，且运动方向偏向罐壁方向，球心方向有少量的浓度分布，与模拟中同时刻相似；30 ms时两侧粉尘云团沿罐壁方向中轴面汇聚，左右两团粉尘云之间有明显的空白区域，同模拟同时刻相似；50 ms前，两侧粉尘云前沿相遇，由壁面碰撞沿着中心对称面向球心扩散，并在球面上有明显的交汇曲线形成，同模拟结果相符。

根据实验实际分散情况也可以推知，在液相与颗粒相相互影响下，液相部分是跟随在粉尘云内部扩散的，由此也可证明模拟得到的液相体积分数的演化规律是符合实际的。

对应时间点的照片上扩散的趋势规律同模拟结果几乎相同，即证明本模拟中得到的20 L球罐内部混合物的分散规律是可信的。

图8 三相分散实验照片Fig.8 The picture of three phase dispersed experimental

以该20 L球型爆炸罐为实验设备，实验条件同模拟条件，探究其混合物爆炸下限，得到表1。

表1 两相和三相的爆炸下限Table 1 Lower explosive limit for two and three phases

注：爆炸为√; 未爆炸为×。

从表1中数据可以看出，对于气固两相混合物来说，点火延迟时间90 ms和100 ms的爆炸下限没有明显区别。对于三相混合物来说，点火延迟时间为90 ms时的爆炸下限明显低于100 ms，由此也证明测量三相混合物爆炸下限的点火延迟时间应该小于两相混合物，即模拟结果是可信的。

3 结论

1)实验工况下，混合物在20 L球罐内部分散时存在由外向内的回流圈，液相的存在会降低粉尘云团的湍流动能并降低其扩散速度，同时增大粉尘云团内部的浓度。

2)实验工况下，测量三相混合物的爆炸下限时，要小于同种气固两相混合物的点火延迟时间10～20 ms，实验结果更为可靠。

3)该数值模型可用来模拟其他种类的三相混合物分散过程，且结果具有一定的参考意义。