允许两辆车驶入的避险车道设置

宋灿灿， 朱桂荣, 郭忠印

(1. 同济大学 道路与交通工程教育部重点实验室，上海 201804； 2. 云南交投集团云岭建设有限公司， 云南 昆明 650224)

避险车道是应对长大纵坡路段货车刹车失灵的最后一道防线，也是有效的工程措施之一.在货车比例较高或交通流量较大的高速公路上，设置允许两辆车驶入的避险车道是非常必要的.

国内外很多学者研究了允许两辆车驶入的避险车道.在美国,修建避险车道的25个州中，8个州发生了多车驶入避险车道的情况[1].新西兰的建设规则[2]和加利福尼亚州的设计指南[3]中均建议采用7.9 m的制动床设计宽度.胡艺馨[4]指出，考虑到两辆车同时自救的避险需求，制动床宽度最小值取8 m.赵含等[5]指出，避险车道的宽度应以能够充分满足短时间内使用避险车道的车辆之间不产生二次事故为标准，根据设计经验，制动床合理的宽度应在4.5～6.0 m.杨永占等[6]通过对71起失控车辆驶入避险车道的横向位置统计得到，失控车辆驶入制动床后与左侧硬路肩的横向净距为1.5～6.0 m，制动坡道宽度建议取值范围为7.5～12.0 m.王磊[7]提出，对于应保证两辆及以上汽车安全驶入的特殊路段，避险车道制动床宽度应控制在8～12 m.刘唐志等[8]指出，由于长下坡货车失事概率较高，在较短的时间段内可能有更多的车辆使用避险车道，因此避险车道制动床宽度最小值应为8 m.朱启合等[9]提出，考虑停放两辆或更多车驶入时，避险车道的宽度宜为9.2～12.2 m.张华[10]提出，对于需要停放两辆或更多车辆的避险车道，理想宽度应为8～12 m.

我国《公路路线设计规范》[11]规定制动床宽度不应小于4.5 m.《新理念公路设计指南》[12]规定，避险车道宽度应足以容纳一辆以上失控车辆和一辆服务车辆，制动床和服务车道的总宽度不宜小于8 m.

美国AASHTO(American Association of State Highway and Transportation Officials)规定，允许两辆车驶入的制动床宽度不低于7.9 m[13].对109条制动床宽度的统计发现，按照美国标准，37%的制动床允许两辆车驶入.我国较多的避险车道考虑了两辆车驶入的工况.

国内外学者并未对允许两辆车先后驶入的避险车道的引道长度进行专项研究.美国高速公路联邦管理局要求引道长度大于305 m[14]，张翱东[15]、孙传夏[16]、宋灿灿等[17]提出引道长度至少达到9、4、6 s设计行程，但并未限定应用于何种横断面宽度.对于允许两辆车先后驶入的避险车道，后车在驶入过程中不仅要判断避险车道的位置，还要判断前车的位置，为避免二次事故，因此需要更长的引道长度.

对于允许两辆车驶入的避险车道，由于我国缺少相关的标准规范，实际应用中出现了两种典型的形式：引道长度过短的短粗型避险车道与引道长度较长的长瘦型避险车道.短粗型避险车道的典型形式是无引道段，而制动床宽度达到12 m及以上，最大宽度为16 m.

本文通过理论建模，研究短粗型避险车道设置的合理性.

1 模型抽象

根据避险车道的制动原理，失控车辆驶入制动床后无法调整方向[18]，因此驾驶员仅能在引道进行行驶方向的调整.避险车道与主线的夹角一般为5°至10°，只有当车辆驶入引道后，驾驶员才能完全看清避险车道的全貌，并做出横向行驶位置的调整.

对于允许两辆车先后驶入的避险车道，后车在主线上行驶时，限于横向与纵向的位置差异，驾驶员难以准确辨别先驶入避险车道车辆的横向停驶位置，即后车只有驶入避险车道引道后，才能完全看清先驶入车辆的停驶位置，后车驾驶员根据前车的停驶位置做出路径的选择，如图1所示.

图1 失控车辆驶入避险车道示意图

通过以上分析可知，当避险车道的渐变段与引道的长度过短时，后车驾驶员没有足够的时间获取前车的位置信息，或有时间获取前车的信息，但缺乏足够的时间进行车辆行驶位置与方向的调整，此时前车、后车在制动床内停驶位置的横向分布可以看作相互独立事件，认为后车的停驶位置不受前车停驶位置的影响.反之，若渐变段与引道的长度足够长，则前车的停驶位置被后车驾驶员获取，并做出相应的横向停驶位置的调整，则前车、后车在制动床上的横向停驶位置为相互影响的连续事件.

2 模型建立

根据模型假设，对于短粗型避险车道，两辆车先后驶入避险车道可作为相互独立事件.根据第一辆车的停驶位置，第二辆车可以成功驶入避险车道的概率分布分为三种情形.

2.1 前车距离左侧护栏较近

如图2所示，a为制动床左侧护栏与X轴起点的距离，l为失控车辆两侧轮胎外边缘间距，b为相邻两辆车轮胎外边缘距离,制动床宽度为9.0 m.当第一辆车轮胎外边缘与X轴起点的距离L在(a+l+b)以内时，第二辆车只有驶入制动床右侧才能避免与第一辆车相撞并且成功地停驶在制动床内.因此,两辆车能成功驶入避险车道的概率

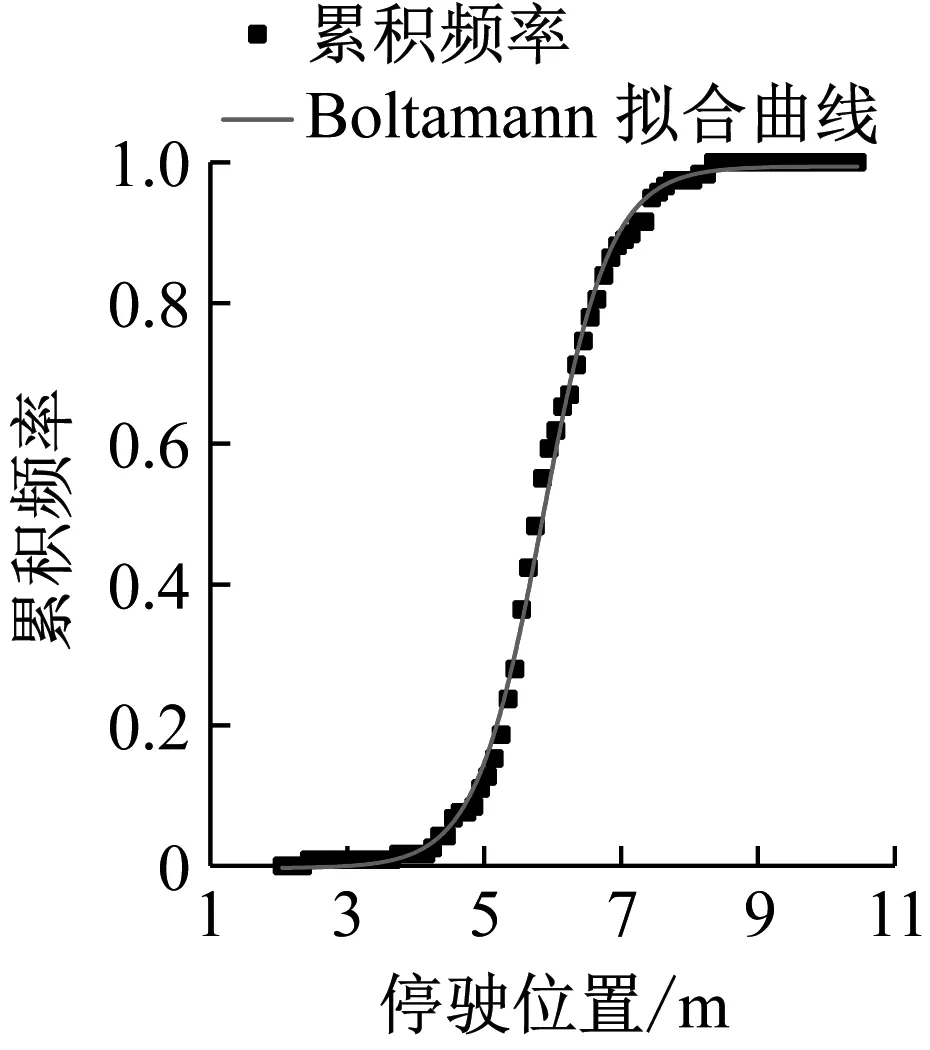
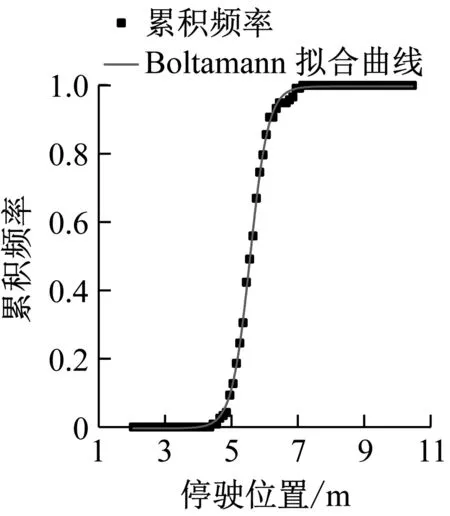
P1=P(X

(1)

图2 前车靠左侧护栏的停驶位置

2.2 前车靠近服务车道

当第一辆车轮胎外边缘与X轴起点的距离为(9.0+a-2l-b)≤L≤(9.0+a-l)时，第二辆车只有停驶在制动床左侧才可成功驶入制动床，如图3所示.因此,两辆车成功驶入避险车道的概率

P2=P(X>x)P(a

(2)

图3 前车靠近服务车道的停驶位置

2.3 车辆停驶于制动床中间

当第一辆车停驶于制动床中间时，(a+l+b)≤L≤(9.0+a-2l-b)，第二辆车既可以停驶于第一辆车的左侧，也可以停驶于制动床的右侧，如图4所示.因此,两辆车成功驶入避险车道的概率

P3=P((a+l+b)≤X

x∈[a+l+b,9.0+a-2l-b)

(3)

图4 前车在制动床中间的停驶位置

综上所述，在假设两辆车先后驶入避险车道的过程完全独立的前提下，两辆车均能成功驶入避险车道的概率

P=

(4)

根据式(4)的边界条件，车辆轮距在2.9 m(车宽3.0 m)以内时，模型有实际意义.对于任意宽度的车辆，在第一辆车成功驶入避险车道的条件下，第二辆车能够成功驶入避险车道的概率

(5)

因此，若计算短粗型避险车道上第二辆车能够成功驶入的概率，需知道车辆驶入避险车道的横向分布概率.

3 横向分布概率建立

采用UC Winroad驾驶模拟仿真平台，获取了驾驶员先后900次驶入避险车道的横向分布数据.实验中，制动床宽为9.0 m，服务车道宽为3.2 m，制动床位于服务车道左侧.设置避险车道的主线线形,包括直线与平曲线，平曲线半径取400～1 000 m，步距取100 m.驶入制动床的车速为90～120 km·h-1，步距10 km·h-1.避险车道的流出角取5°～30°，步距取5°.共168个设置水平.

实验拖挂车宽2.5 m(包含后视镜)、长12.0 m，车轮外距2.4 m，如图5所示.通过车辆轮胎外边缘距道路左侧护栏的最小距离判断车辆停驶位置.根据避险车道的横断面组成(见图5，护栏(0.18 m)+路缘石(0.2 m)+制动床(9.0 m)+服务车道(3.2 m)+路缘石(0.2 m)+护栏(0.18 m))，车辆停驶于制动床的范围为[0.38,6.98] m，车辆停驶于制动床与服务车道的范围为(6.98,9.38] m，车辆停驶于服务车道的范围为(9.38,10.18] m.

图5 驾驶模拟实验车与道路模型

根据实验设计，驶入车速、主线线形与流出角均可能对车辆停驶位置的概率分布产生影响，因此采用多因素方差分析确定影响因素.多因素方差分析需要满足正态性、方差齐性和协方差球形性三个使用条件.通过夏皮罗-威尔克方法对数据的正态性检验得出P>0.05，数据服从正态分布.通过方差齐性检验发现P<0.01，各水平方差不齐.因此，多重事后检验时选择两个组方差不等的Dunnet C检验方法.球形性检验发现，除驶入车速的P=0.077>0.05，流出角、主线线形与三者之间的交互作用项均不满足球形性假设检验.

驶入车速的样本协方差服从球形性假设，因此适合一元方差分析；流出角、主线线形样本协方差不服从球形性假设，因此采用GG(Greenhouse-Geisser Epsilon)校正来检验结果.个体内部变异部分的计算结果显示，主线线形对车辆停驶的横向位置有显著影响(P=0.01<0.05)，驶入车速、流出角及三者之间的交互作用对车辆的停驶位置不存在显著影响.不同主线线形的对比发现，主线线形为直线与平曲线时车辆的停驶位置存在显著差异，不同平曲线半径的停驶位置差异不明显.因此，需根据不同的平曲线半径建立车辆横向位置的概率分布函数.

对不同平曲线半径车辆停驶位置进行统计，如表1所示.主线线形为直线与平曲线半径不低于700 m时的停驶位置平均值相同，与平曲线半径低于700 m时的停驶位置平均值的差异也不大.主线线形为直线时与平曲线半径为400 m时的离散度基本一致，均比其他平曲线半径对应的离散度大.不同条件下变异系数差异明显，主线线形为直线时与平曲线半径不大于600 m时的变异系数接近，平曲线半径介于700 m至1 000 m时的平曲线变异系数明显低于主线线形为直线时.

表1 直线和不同平曲线半径下停驶位置统计

对不同平曲线半径，通过Boltamann曲线拟合失控车辆在制动床内的横向分布函数，如图6所示.通过卡方检验来检验曲线的拟合优度，如表2所示.除半径800 m的平曲线外，其他条件下失控车辆横向停驶位置的累积频率曲线均符合Boltamann曲线.

表2 直线和不同平曲线半径下累积频率曲线拟合检验

4 结果分析

限于函数的复杂性，将累积频率拟合曲线代入模型后，采用Matlab软件对函数进行近似计算，如图7所示.由图7可知，无论主线线形采用何种参数设置，第二辆车驶入避险车道的成功概率均呈双峰曲面变化，这与实际相符，即第一辆车停在制动床一侧时，第二辆车成功驶入制动床的概率提高，而第一辆车停在制动床中间时，第二辆车成功驶入制动床的概率降低.第一辆车停放于制动床外侧时，第二辆车成功驶入制动床的概率最高.

a 400 m

b 500 m

c 600 m

d 700 m

e 800 m

f 900 m

g 1 000 m

h 直线

图6 直线和不同平曲线半径下车辆横向停驶位置累积频率拟合曲线

Fig.6 Cumulative frequency fitting curve of vehicle transverse stopping position under straightline and different circular curve radii

对不同车辆宽度条件下第二辆车能够成功驶入避险车道的概率求积分，即可得到多次不同车辆成功驶入避险车道的概率，如图8所示.随着平曲线半径的增大，车辆成功驶入避险车道的概率整体上呈增大的趋势;随着车辆宽度的增大，车辆成功驶入避险车道的概率整体上呈减小的趋势.对比主线线形为直线的路段与平曲线的路段，主线线形为直线时车辆成功驶入避险车道的概率明显高于主线线形为平曲线时，但是通过概率绝对值可以看到，即使是在主线线形为直线的条件下，车辆成功驶入避险车道的概率也较低.横向比较可以看到，当制动床宽度为9.0 m、车宽为1.8 m时，制动床宽度取值为车宽的5倍，车辆成功驶入制动床的概率仍然不超过15%，说明仅通过拓宽制动床宽度而不设置满足长度要求的引道，不能保证第二辆车能够成功驶入制动床.

5 结语

针对我国广泛采用的允许两辆车驶入的避险车道的典型形式之一，通过对设置较短或不设置引道以及超宽制动床的避险车道研究发现，允许两辆车先后驶入的避险车道受主线线形的影响显著，并且仅拓宽制动床不能达到有效提高两辆车成功驶入避险车道的目的.

根据制动床原理，驾驶员只有在驶入制动床之前才能调整车辆的行驶方向，因此在允许两辆车先后驶入的避险车道上必须设置较长的引道，提供给后车足够的空间以调整车辆的方向.

a 400 m

b 500 m

c 600 m

d 700 m

e 800 m

f 900 m

g 1 000 m

h 直线

图7 直线和不同平曲线半径下第二辆车能够成功驶入避险车道的概率分布

Fig.7 Probability distribution of the second vehicle successfully entering truck escape ramp under straightline and different circular curve radii

图8 直线和不同平曲线半径下车辆成功驶入避险车道的概率分布

Fig.8 Probability distribution of vehicle successfully entering truck escape ramp under straight line and different circular curve radii

本文中未给出允许两辆车先后驶入的避险车道引道长度的设置标准，是后续研究的重要方向之一.