平面组合图形面积的求法研究及其推广

吴菊青

摘要：在“组合图形的面积”这一课的教学中，发现学生对求解组合图形的面积感到非常吃力，经常无从下手。为了提高学生的解题能力，除了让学生们加强对应的练习以外，还应该教给他们一定的解此类题目的技巧。本文介绍几种常用的方法--分割法、添补法、平移交换法等，供大家学习参考。

关键词：平面;组合图形;面积;探究

一、对平面图形的认识

（一）平面几何图形的认识

平面几何图形能使学生感受到图形美，帮助学生认识丰富多彩的现实生活中的各种实物，形成一定的空间观念。小学阶段接触到的平面图形面积分tt为七部分内容：三角形的面积，正方形的面积，长方形的面积，平行四边形的面积，梯形的面积，组合图形的面积，圆的面积。在《课程标准（2011）》的内容分类中属于“图形与几何”的范畴，而平面图形的面积则是“图形与几何”这部分中的重点内容。这部分的教学目标是：教学紧密联系现实生活，让学生通过动手操作，掌握各种平面图形的面积计算公式的推导过程，并会应用面积公式来正确计算对应平面图形的面积，解决一些简单的有关平面几何图形的面积问题，从而形成了一个从现实生活到数学知识，再回到现实生活的过程。同时值得指出的是，平面图形面积的学习也是学习立体图形表面积和体积的基础。

（二）小学阶段的平面几何知识各年级内容安排

一年级下册：会辨认并能区分长方形、正方形、平行四边形、三角形和圆;通过找一找、画一画、拼一拼、摆一摆各种平面图形，感受它们的特征以及之间内在联系和区别。

三年级下册：初步理解面积的含义，并会用简单的语言来描述面积的概念;理解的基础上，推导长方形和正方形的面积公式，并掌握其计算方法，同时会运用长方形和正方形的面积公式解决一些简单的实际生活中的问题。这部分知识是学生第一次接触有关面的内容，并且比较抽象。理解面积的概念时，要以具体、形象的实物让学生摸一摸，并说说摸到的实物表面具有怎么的特征，感受、讨论之后总结出什么是面积这一抽象感念，其后掌握了面积单位之间的换算。长方形和正方形的面积是在掌握了这部分知识和他们的基本特征的基础上来学习的。在教学过程中教师可以指导学生小组合作，用1cm2的小正方形纸片“满贴”长方形和正方形的物体的表面，数出小正方形纸片的个数，就是长方形和正方形的面积，观察小正方形纸片的个数，横着有几个，竖着有几个，发现“满贴”长方形和正方形的物体的表面纸片的个数与长方形和正方形的面积之间的关系，从而总结他们的面积公式。让学生的手、口、耳、眼等感官全都动起来，有效的提高所学知识的效果，并在小组合作交流的过程中自己总结出所学知识的要点，获得成就感的同时激发数学学习兴趣和求知欲。

五年级上册：引导学生利用方格纸和割补法、拼组法等转换思想的方法探索平行四边形、三角形、梯形的面积计算式;掌握并会应用它们的面积来解决简单的实际生活问题。认识组合图形，并会将组合图形划分为己学过的图形来计算面积。三角形和梯形面积公式推导是借助平行四边形的面积公式和推导原理完成的，并会将平行四边形、三角形和梯形的面积公式准确的运用到现实生活中，这些平面圖形的面积计算方法和推导过程是进一步学习圆面积以及立体图形表面积和体积的基础。

学生在学习了长方形、正方形、平行四边形、三角形和梯形的面积的计算方法后，再来学习组合图形的面积就比较方便了。把一个组合图形在其面积不变的情况下分解成若干个学生己经学过的基本平面图形，再来进行计算各部分的面积，组合图形的面积就是分解后的各部分图形面积之和。这样的教学安排让学生进一步巩固了该些基本平面图形的特征和面积公式的运用，同时还发展了学生的空间观念。这样新知识与旧知识之间的联系，根据图形面积计算之间的内在联系来安排的教学顺序，可从促进学生对知识的迁移和学习能力的提高。

六年级上册：在认识圆的基础上掌握圆的基本特征;学会用圆规画圆;会推导并正确应用圆的周长和面积。学生已经掌握了长方形、正方形、平行四边形、三角形、梯形的周长和面积计算方法，对圆己经有了初步的了解的基础上进来学习圆的周长和面积。圆是一种曲线图形而不是直线图形，和以前学的直线图形在性质和特征上有截然不同的区别，但在研究方法上，又与直线图形紧密联系，因此在教学时教师要不断引导学生应用转化思想，将圆转化成以前学习过的直线图形，再用割补法、拼组法等转化方法，来解决圆的面积。本单元主要认识圆，掌握圆的基本特征，理解圆的直径、半径、周长、面积之间的相互关系：知道圆周率的由来和近似值;运用所学知识来解决现实生活中有关圆的一些实际问题。丰富学生对现实生活在“空间与几何”图形的认识，进一步建立空间观念，发展空间想象为和形象思维。通过介绍祖冲之及国外学者在圆周率方面的研究成就，了解与其有关的数学史，加强对学生的爱国主义教育。让学生体验到圆是与日常的现实生活是密切联系在一起的，认识到用圆的知识可解决很多现实生活中的问题。

平面：中学几何课本中常以平静的湖面和平滑的桌面等描述平面。在小学阶段一般用手感受光滑的物体表面，来形容平面。

平面图形：图形上的所有点都在同一个平面上，这样的几何图形叫做平面图形。

几何图形：简称“图形”。有点、线、面、体或有若干个点、线、面、体组合在一起的图形，叫做几何图形。

二、求组合图形面积的方法

在“组合图形的面积”这一课的教学中，发现学生对组合图形的面积的如何求解感到非常吃力，无从下手。为了提高学生的解题能力，除了让学生加强练习以外，还应教给他们一定的解题技巧。下面介绍几种常用的方法——分割法、添补法、平移交换法等，供大家参考。

（一）分割法

例1：如右图，求下面组合图形（每个角都是直角）的面积.

①把例1中的组合图形分割成2个长方形（或者正方形），如

=4×6=24cm2，=3×（7-4）= 9cm2， S=+=24+9=33cm2

②把该组合图形分割成2个梯形

=（3+6）×4÷2=18cm2， =（3+7）×3÷2=15cm2， S =+=18+15=33cm2

（二）添补法

将此组合补上一个小长方形（或小正方形），就可以补成一个大的长方形，从而求组合图形的面积可以转换成求大长方形的面积减去小长方形（或小正方形）的面积。

=6×7=42cm2， =3×3=9cm2， S =―=42―9=33cm2

以上两种方法可以合起来简称为“割补法”。割补法是指;把一个图形的某一部分割下来，填补在此图形的另一部分，在原来面积不变的情况下，使其转化为已经掌握的基本图形，以利于计算公式的推导。

但是要注意的是，在分解组合图形时，分割后的图形要让人一看就懂，简单明了。

（三）其他方法

平移变换法：把组合图形中的一部分图形位置作水平移动，使之与组合图形中的其他部分合并，拼成一个较简单的组合图形，然后求出它的面积，这种方法我们称为“平移变换法”

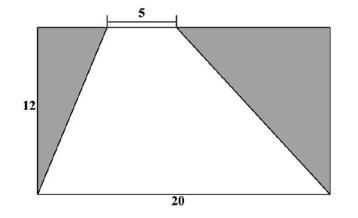
例2：求下面图形阴影部分的面积。〔单位：厘米〕

分析可以得出，两个带有阴影部分的三角形都是直角三角形，并且其中有一条直角边是相同的，那么我们就可以把小的直角三角形向右平移，与大的直角三角形拼在一起，如下图，于是所拼得的大三角形面积，刚好是所要求的阴影部分的面积。

解：（20-5）×12÷2=15×12÷2=90（平方厘米）

旋转变换法：有些图形问题条件比较分散。若能设法把图形绕一个定点，在平面内旋转一定的角度，使图形的某部分移动至一个新的位置，往往能使原本分散的条件集中，从而使问题化难为易。

例3.如图，是一个长方形挖去了一个三角形，点G是两平行线之间的任意一点，请求出下面图形的阴影部分的面积。

分析：由于点G是两平行线之间的任意一点，上下两部分阴影部分的都是三角形，如果分别求出每个阴影部分三角形的面积，再相加求总的面积，可是问题的关键是上下两个三角形的高的长度不是固定的，为了方便，我们给每个点编号如下图1：

由于三角形面积计算只与该三角形的底边长度以及高线长度有关，所以可以转换成图2，只要求出了图2的阴影部分面积总和，也就求出了图1的阴影面积总和.

=AD×DG，  =BC×GC，AD=BC

+=AD×DG+BC×CG=AD×DG+AD×CG=AD×（DG+CG）

∴+=AD×DC =AD×AB=×10×6=30

参考文献：

[1]王明菊.小学平面图形面积教学研究[D].内蒙古师范大学，2015.

[2]谢鼓平.小学教案与教学设计数学.六年级（上）[M].乌鲁木齐：新疆青少年出版社，2013：110-149.

[3]陈森林.简明数学辞典[M]. 武汉：湖北人民出版社，1984：184-185.

[4]黃文选，刘梦想，方金秋. 小学教师实用数学辞典[M].北京：北京科学技术出版社， 1997：268

[5] 李天林.组合图形面积的计算技巧[J].河北教研，1999，（05）：33-34.

[6]五年级上册数学.义务教务教科书. 北京师范大学出版社，2013.