遗传算法优化BP神经网络在太阳散射辐射估算领域的应用

苏 刚，郝浩东 ，席 悦，车克南

（1.天津城建大学，天津 300384；2.天津华泰清源环境技术有限公司，天津 300384）

近年来，随着人类生活水平的日益提高及能源危机的加剧，新能源的重要性日益凸显，太阳能因其可再生、无污染及分布范围广等特点，受到了世界各国的青睐[1-2].太阳能资源评估、光热、光伏及建筑能耗估算等领域迫切需要精确的太阳辐射，尤其是太阳散射辐射数据[3].然而，由于仪器购置及维护费用昂贵，在许多地区（尤其是发展中国家和欠发达地区）缺少长期的太阳散射辐射观测数据[4].因此，建立精确的太阳散射辐射估算模型尤为重要[5-6].本文提出了一种太阳散射辐射估算新模型，采用遗传算法优化BP神经网络，弥补BP神经网络中存在的缺陷，提升太阳散射辐射模型的准确性及适用性，为广大发展中国家及欠发达地区提供精确的太阳散射辐射估算模型，为太阳能资源开发及利用等领域提供准确的太阳散射辐射数据.

1 遗传优化算法

1.1 BP神经网络

BP神经网络可从训练样本中学习并存储输入和输出之间对应的映射关系，而不需要给出两者具体的数学方程.BP神经网络由输入神经元、输出神经元和隐含层神经元3类神经元组成，其中：输入神经元接收外部输入信号及数据；输出神经元输出网络对数据的处理结果；隐含层神经元则位于输入和输出神经元中间，外部无法直接观察.不同神经元之间的连接权重反映了彼此之间影响关系的强弱，BP神经网络通过神经元彼此之间的连接关系来实现对输入数据的处理.BP神经网络隐含层可以是一层或多层，只要隐含层具有足够数量的神经元，3层神经元网络结构即可实现任意数量的输入与输出的映射关系.图1为一个包含两层隐含层的BP神经网络拓扑结构.

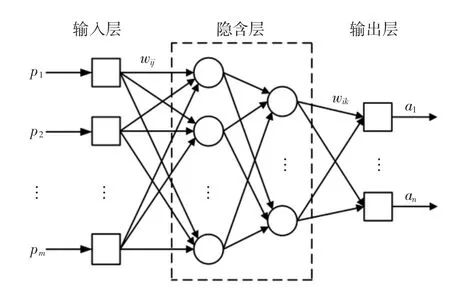
图1 BP神经网络拓扑结构图

1.2 遗传算法

遗传算法（genetic algorithms）是基于自然界生物种群遗传机制和物种进化理论构建的一种并行随机搜索最优化方法，将生物进化原理中“优胜劣汰，适者生存”的思想引入算法中.遗传算法通过种群初始化过程将待求参数编码至串联群体中；通过选择、交叉和变异遗传操作来并行随机搜索最优待求参数，基于选定的适应度函数对群体中的个体进行筛选，淘汰适应度差的个体，保留适应度好的个体，循环往复，使新种群在继承上一代优良信息的基础上更优于上一代，直至满足设定的循环停止条件.

1.3 基于遗传算法优化的BP神经网络（GA-BP）

尽管BP神经网络在非线性、大数据量、多变量及输入输出具体映射关系未知的函数回归及数据分析领域表现优良，但其仍然存在许多缺陷，如网络结构最优参数难以确定、收敛时间过长及极易陷入局部寻优的困境等.遗传算法作为一种并行搜索全局寻优的算法可以有效解决BP神经网络存在的网络结构最优参数难以确定及极易陷入局部寻优的缺陷，进而解决BP神经网络收敛时间过长的问题.图2为基于遗传算法优化的BP神经网络基本流程.

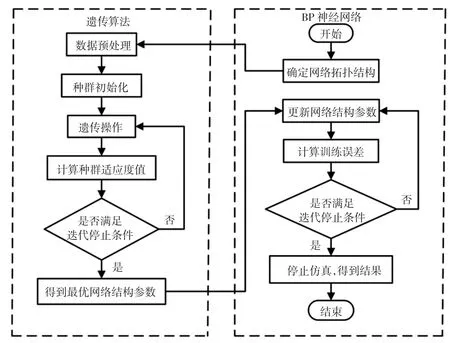
图2 遗传算法优化BP神经网络流程图

传统BP神经网络最优网络结构参数难以确定，在根据网络结构随机生成网络结构参数后，基于反向传播算法经过多次迭代之后才能确定最优的网络结构参数，在这个过程中，还存在极易陷入局部寻优困局的缺陷.为此，本文使用遗传算法来优化传统BP神经网络的网络结构参数寻优部分，基于遗传算法全局并行搜索的特性可以帮助BP神经网络快速找到最优网络结构参数，大幅缩减收敛时间且避免BP神经网络在训练时陷入局部寻优的困局，实现传统BP神经网络的优化.

遗传算法优化BP神经网络的具体实施步骤如下.

（1）种群初始化

种群初始化即将待求参数进行编码，编码方式主要有二进制编码、实数编码和排列编码.本文采用二进制编码方式，将待求参数编码为串联二进制代码，主要目的是为了将实际问题程序化，便于计算机求解.

（2）适应度函数的选择

适应度函数应根据具体问题进行选择，其类似于物种进化论中大自然的选择过程，通过种群中个体适应值的大小来判断种群中不同个体适应能力的强弱，即待求参数的优劣，适应度函数的选择应考虑计算简单及满足问题要求等因素.本文遗传算法部分采用构建好的BP神经网络计算误差为适应度函数，适应值越小表明待求参数越好，其具体计算公式为

式中：n为训练集中的数据组数；mi为每天太阳散射辐射的实际测量值；ci为BP神经网络的计算值.

（3）遗传操作

遗传操作有选择、交叉和变异3种操作，类似于生物遗传机制中的基因选择、交叉和变异的概念.选择操作有轮盘赌法、锦标赛法等多种方法，主要负责两代种群之间信息的传递；交叉操作则体现了种群不同个体之间信息的相互交换；变异操作则体现了个体信息的突变，实现种群包含信息的改变.基于选择、交叉和变异这3种遗传操作，可以通过并行搜索实现待求参数在解集范围内的全局寻优，提高寻优效率，缩减网络收敛时间.

太阳散射辐射作为太阳辐射数据中最重要的一类数据，影响因素众多，时至今日，国内外的研究学者提出了基于不同影响因素、形式各异的太阳散射辐射估算模型，也取得了一定的效果，但这些模型存在一些普遍的问题，如适用性差、估算准确性低及计算时间过长等.而基于遗传算法优化的BP神经网络则可以很好地解决具体影响因素不确定、计算时间过长及适用性差的问题，非常适合用于解决太阳散射辐射的估算难题.

2 案例研究

某市位于东经 115.7°～117.4°，北纬 39.4°～41.6°，平均海拔43.5 m.本文收集整理了某市从1993年1月至2017年5月的平均晴空指数、日照百分率、相对湿度、平均气温、最高气温及最低气温共24 a的日值气象数据，剔除由于设备保养、机器维修及采集失误导致的异常数据，得到8 519组数据，对剔除异常值后的数据进行了归一化处理，使用其中8 362组数据作为训练数据，157组数据作为验证数据，将平均晴空指数、日照百分率、相对湿度、平均气温、最高气温及最低气温6种气象参数作为输入，日太阳散射辐射作为输出来构建BP神经网络，并基于遗传算法来优化网络结构初始参数，进而构建了基于遗传算法优化的BP神经网络太阳散射辐射估算模型.此外，本文将构建的新模型与传统BP神经网络模型和相关文献中既有经验模型（见表1）进行了对比分析，来论证新模型的优劣.

表1 经验模型计算方法

本文使用平均绝对误差、均方根误差、相对均方根误差及相关系数来分析基于遗传算法优化BP神经网络太阳散射辐射估算模型的精确性，表2列出了基于遗传算法优化的BP神经网络太阳散射辐射估算模型、传统BP神经网络模型和既有经验模型估算结果的相关统计参数，图3则展示了不同模型估算误差的箱型分布图.

表2 不同模型统计参数值

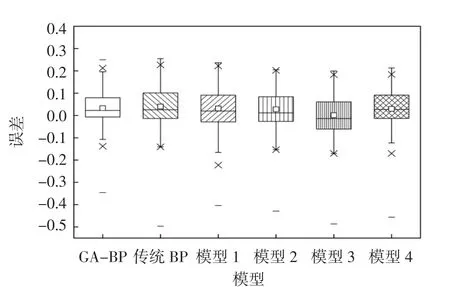
图3 不同模型的误差箱型图

由表2可知，基于遗传算法优化BP神经网络太阳散射辐射估算模型相较于传统BP神经网络模型和4个既有经验模型中的平均绝对误差、均方根误差及相对均方根误差3个误差统计参数最小者，分别降低了14%，11%及11%，而相对于5个经验模型中相关系数最大者，相关系数增大了1.5%.从图3中可以看出，在反应误差主体分布范围大小的箱体高度比较上，GA-BP模型占据绝对领先地位，因为其箱体高度在所有模型中最窄，表明基于遗传算法优化BP神经网络太阳散射辐射估算模型的准确性最高.图3中不同模型箱体中间的横线和小方框分别代表不同模型估算误差的中位数，可以看出基于遗传算法优化BP神经网络太阳散射辐射估算模型估算误差的中位数与平均数相较于其他模型要更接近于零，同样证明了基于遗传算法优化BP神经网络对太阳散射辐射的估算准确性相较于其他模型要更好.结合表2和图3可以表明，该模型对太阳散射辐射的估算精确度要高于既有经验模型，且本文选取的输入参数（平均晴空指数、日照百分率、相对湿度、平均气温、最高气温及最低气温）与太阳散射辐射相关性比既有经验模型的输入参数（晴空指数）更高，因此本文构建的新模型要优于上述5个既有经验模型.

3 结论

（1）基于遗传算法优化传统BP神经网络，弥补了传统BP神经网络结构参数难以确定、收敛时间过长及极易陷入局部寻优困局的缺陷.

（2）以平均晴空指数、日照百分率、相对湿度、平均气温、最高气温及最低气温6种常规气象参数作为输入参数，日散射比作为输出结果构建了基于遗传算法优化BP神经网络的太阳散射辐射估算模型，并计算了其对应的统计参数，相关系数值为0.961 95，平均绝对误差为0.056 01，均方根误差为0.077 79，相对均方根误差为0.001 12.

（3）将基于遗传算法优化BP神经网络太阳散射辐射新模型与传统BP神经网络模型和4个既有经验模型进行了对比，相较于其他模型，相关系数增大了1.5%，平均绝对误差降低了14%，均方根误差降低了11%，相对均方根误差也降低了11%，表明新模型的精度更高.