岩石节理粗糙度新指标及新的JRC确定方法

班力壬，戚承志，燕发源，刘 源，朱 淳，陶志刚

(1.中国矿业大学(北京) 力学与建筑工程学院，北京 100083; 2.北京建筑大学 北京未来城市设计高精尖中心，北京 100044; 3.北京建筑大学 2011节能减排协同创新中心，北京 100044; 4.天津科技大学 机械工程学院，天津 300222)

岩石节理剪切强度对煤矿建设工程、大型水利水电设施安全、核废料地质储存工程等岩石工程安全与稳定有重大影响[1-4]。岩石节理只是在节理面接触，因而与完整岩石力学性质差别很大。节理面的粗糙度影响真实的接触面积，进而对节理剪切力学性质有重要作用[5]。描述岩石节理粗糙度的方法主要可分为统计参数描述、分形描述、JRC曲线描述等[6]。

统计参数描述是将节理形貌线等效为具有一定间距的离散点，对其位置信息进行数学上的统计分析。常用统计参数有高度均方根z1、均方根Z2、剖面指数Rp、形貌线伸长指数δ等[7]。节理轮廓具有统计意义上的自相似，具有分形特点。节理形貌线的分形维数会随着测量尺度r变化而变化，当测量尺度小到一定值时所得分形维数才获得稳定。而此时所测量的形貌细节对岩石节理力学性质的影响已经很微弱，因此仅用分形维数很难与岩石节理面剪切强度联系起来[6]。BARTON[8]提出了10条标准JRC曲线，这10条标准JRC曲线是最常用的描述岩石节理面粗糙度的方法。确定JRC的方法有视觉对比法、统计参量联系法、分形维数联系法、BARTON直边法等[9-12]。

以上粗糙度指标都是二维粗糙度指标，由于形貌线信息量不足的限制不能完全表示岩石节理形貌面的粗糙程度，并且都不能表示岩石形貌的剪切方向性。粗糙度指标大多对尺度比较敏感，对于不同的测量尺度获得的粗糙度指标不同。GRASSELLI提出了一个三维粗糙度指标，该指标可以很好的与节理剪切强度联系起来，并且可以表征形貌面各向异性[13]。但是不同的网格密度获得粗糙度指标不同，在应用时必须严格按照指定的网格密度获取粗糙度指标，这一特点使得粗糙度指标在应用上不方便，对仪器精度要求较高。

虽然三维指标可以更好的表示形貌面的真实粗糙度，但是二维粗糙度指标也有自己的优势:提取简单，数据处理方便。将三维形貌面指标思想用于二维，在实际工程中多测几道平行形貌线也可以达到很好的精度。形貌线只有2个分析方向：正向与反向。剪切方向与形貌线共线，所以计算节理角度时工作量大大简化，更适用于工程应用。因此二维粗糙度指标的研究也不能放弃。TATONE在GRASSELLI研究的基础上将三维指标应用于二维形貌线上提出了能够反映剪切方向性的二维指标[14]。但GRASSELLI提出的三维粗糙度指标本身在计算过程中具有一定的主观性，并且不能合理表示出节理面爬坡面积相同而背坡面积不同的情况。采样间距不同也是获得不同的粗糙度指标。

笔者分析了GRASSELLI粗糙度指标的局限性，在长方体微凸体的基础上提出一个具有方向性的粗糙度指标，该指标可以反映岩石节理剪切性能，同时可以表示出形貌面各向异性。在不同的测量尺度下该指标具有不同的数值。基于分形思想，放松了采样间距获取指标的限制，获得了不受测量尺度影响的岩石节理粗糙度评价系统。

1 GRASSELLI粗糙度指标的局限性

GRASSELLI首次将岩石三维形貌面参数与节理面剪切强度联系起来。形貌面三维描述的方法首先通过光学非接触式形貌扫描仪获得节理微元节点的位置坐标，然后通过一定间距形成三角形单元。通过计算三角形单元的特征参数来得到三维形貌参数。研究表明:只有面向剪切方向坡度角为正的节理微元对剪切强度有贡献。有效倾角大于θ*的所有微元面积比Aθ*与θ*之间的关系[13]为

(1)

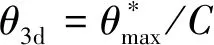
GRASSELLI提出接触面积比Aθ*为所有有效倾角不小于θ*的所有微元面积总和Ad与节理面总面积At的比值。

(2)

对于三维化的网格

(3)

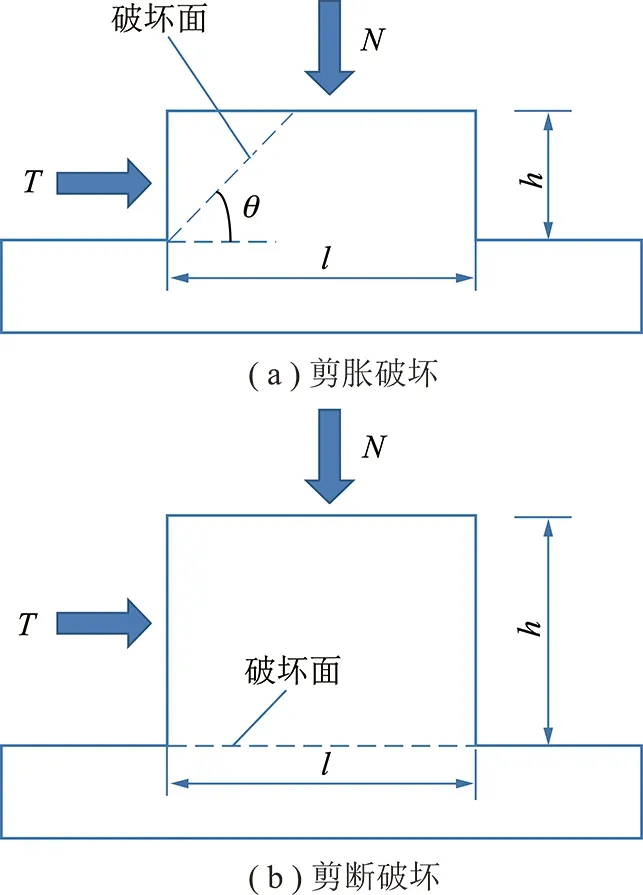
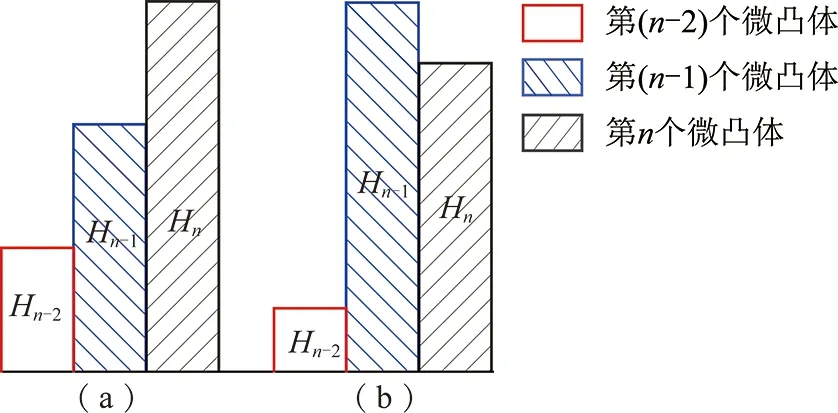
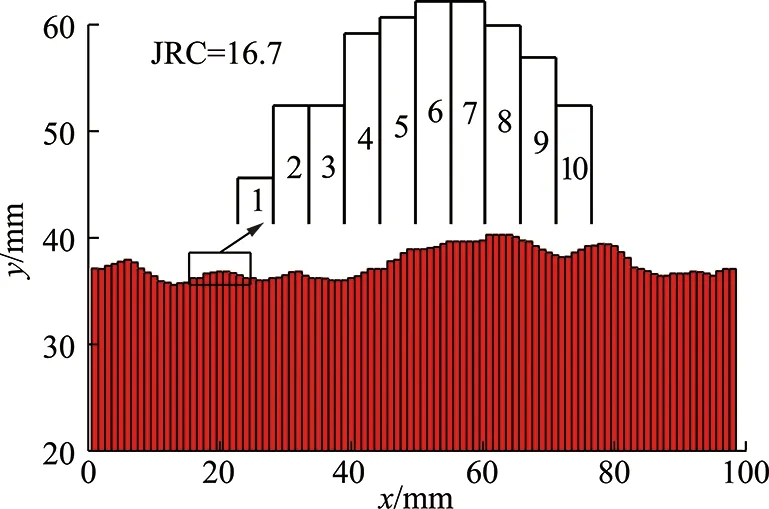
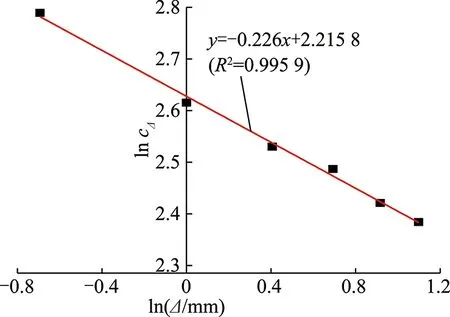
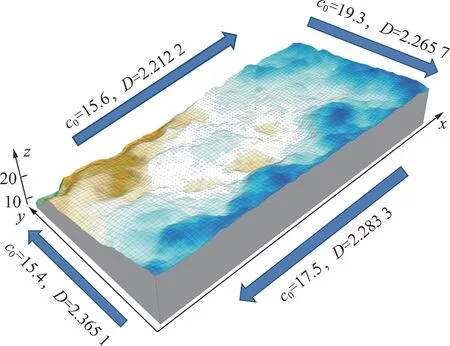
其中，Nx，Ny分别为沿x，y轴取样数目;Δx，Δy分别为沿x，y轴取样间隔;zi,j为采样点(i,j)的高度。采用接触面积比Aθ*可以反映形貌的特点，其范围为0

图1中剪切方向为由左向右。两组节理面爬坡区域相同(假设爬坡区域面积均为3)，背坡区域不同(假设背坡区域面积分别为3，5)。节理力学性质只与爬坡区域有关，背坡区域并不影响剪切力学性质，所以图1中两组节理面剪切力学性质是相同的。合理反映节理面剪切强度的粗糙度指标在这种情况下应该是相同的，但是采用接触面积比Aθ*假设此时θ*=0，也就是A0来表示上述2种情况所得数值不同，分别为1/2与3/8。这就不能很好的与节理面剪切强度联系起来。

图1 2种类型微凸体Fig.1 Two types of asperity

TATONE提出的二维指标是在以上基础上将面积改为形貌线长度获取的二维指标，也存在以上4个问题。采用统计倾角拟合获取粗糙度参数具有一定的主观性，若是改变思路将节理微元等效为长方体微凸体，以长方体微凸体高差表征粗糙度可以克服以上问题。

2 描述岩石形貌面粗糙度新指标c

长方体微凸体根据几何参数与边界条件不同可发生2种破坏模式的破坏[15]。如图2所示长方体微凸体高度为h，长度为l，几何参数m=h/l，法向荷载为N，切向荷载为T。当mmc时为剪断破坏(图2(b))。

图2 长方体微凸体破坏模式Fig.2 Failure modes of rectangular-shaped asperity

其中临界几何参量mc为

(4)

其中，σn为微凸体顶部法向应力;c，φf分别为完整岩石的黏聚力与峰值摩擦角。长方体微凸体的剪切强度τ为

(5)

当m

将节理面按照一定网格密度等效为一系列连续的长方体微凸体，若提出一种确定其计算高度的方法则可预测其剪切强度。2种特殊形式排列的长方体微凸体如图3所示，剪切方向为从左到右。充分考虑沿剪切方向微凸体相对凸出部分为贡献高度以及考虑第n-1与第n-2个微凸体的影响可确定第n个微凸体计算高度hn为

hn=max((2Hn-Hn-1-Hn-2)/2,0)

(6)

式中，Hn为第n个微凸体高度。

图3 长方体微凸体2种排列模式Fig.3 Arrangement modes of rectangular-sharped asperities

图3仅列举了2种典型排列情况来阐述计算高度确定方法。对于其他微凸体排列情况，也是用式(6)计算。第n个微凸体计算高度物理意义为考虑第n-1与n-2个微凸体影响的沿剪切方向为正值的高差。

在上述分析基础上将微凸体计算高度指标化取

(7)

其中，N为微凸体总数;L为沿剪切方向的节理面长度。描述形貌粗糙度新指标c的物理意义是沿形貌剪切方向对剪切强度有贡献微凸体的平均坡度角，若将节理面简化为PATTON研究的齿形节理面[16]，则指标c代表的就是100tani，其中i为规则齿形节理角度。粗糙度指标c可以将形貌面客观表示出，同时剪切方向不同时对应的指标c不同。指标c是由长方体微凸体2种破坏模式结合一种确定长方体计算长度的模型得到，可以将节理几何特征与剪切强度结合起来，进而将节理粗糙度与节理剪切强度结合起来，这就为考虑剪切方向性的岩石节理剪切强度公式的提出提供可能。

3 计算标准JRC曲线的c指标

3.1 获取标准曲线上节点坐标信息

基于图像分割技术可提取标准JRC曲线坐标信息。将每条标准JRC曲线以图片形式保存，采用Getdata软件中区域数字化功能，将网格设置为0.5 mm。确定好x，y方向标度就可以得到曲线上间距为0.5 mm节点的位置坐标。目前提取节点位置信息是基于印刷版本曲线，在印刷过程中由于排版问题会出现曲线与标尺不在一条直线的情况。通过线性拟合所得节点可以得到拟合直线，检查拟合直线是否与标尺平行。若不平行则需调整曲线使之与标尺平行。然后再求得调整相应角度后曲线的每一点的位置坐标。此时所得曲线上节点的坐标即可代表曲线的信息。

3.2验证所提取坐标准确性

坡度均方根

(8)

其中，L为形貌线长度;Δx为取样间距;M为取样总数。对于特定曲线采样间距一致时Z2值一定。计算基于3.1节所提取标准JRC曲线的Z2，并将其与TSE等[9]，YANG 等[17]，YU等[18]的研究结果对比可以判断所提取数据是否真实的反映了形貌线的特征。

由图4可知，在采样间距为0.5，1 mm所取数据得出的Z2与已有研究结果基本一致。证明3.1节提取数据方法可以很好的反映曲线的真实粗糙度，具有一定的可信度。

图4 本文试验所得结果与已有试验结果对比Fig.4 Z2 obtained by current study and previous studies

3.3 计算粗糙度指标c

本节以JRC=16.7曲线为例，说明计算粗糙度指标c的过程。在采样间距为1 mm的情况下，结合3.1与3.2节内容确定出曲线上节点的坐标。以节点为矩形微凸体顶点中心，宽度为1 mm画出每一个采样点对应的矩形微凸体，如图5中红色柱状图所示，微凸体顶点连线近似代表JRC=16.7曲线。将曲线局部放大，并对部分微凸体编号(图5中无填充柱状图)。若局部1号微凸体为整条曲线第一个微凸体，假设其计算高度为0。2号微凸体由于前面只有一个微凸体，根据式(6)计算高度h1=max(H2-H1,0)。3号微凸体由于前面有2个微凸体，考虑两个微凸体影响，根据式(6)计算高度h3=max((2H3-H2-H1)/2,0)。其余后面微凸体计算高度均按式(6)得出。得到每个微凸体计算高度后，按式(7)得到JRC=16.7曲线粗糙度指标c值为13.67。其他标准JRC曲线的参数c计算方法类似，所得结果(采样间距1 mm)见表1。

图5 采样间距为1 mm的JRC=16.7曲线微凸体示意Fig.5 ASPERITIES of JRC=16.7 profile with the sampling interval of 1 mm红色部分为矩形微凸体组成的JRC=16.7曲线，左侧高度轴只对红色区域有效

表1 采样间距为1 mm的标准JRC曲线的c值Table 1 Value of c of each standard JRC profile with the sampling interval of 1 mm

表1中第2列JRC的精确值是由试验反算求得[8]。由表1可知，不同JRC曲线对应不同的c值，随着JRC值增大，c值也在增大。相同的JRC曲线，不同方向分析所得c值不同，这就为提出具有方向性的节理面剪切强度公式创造条件。

4 不受采样间距影响的粗糙度评价系统

4.1 采样间距对粗糙度指标c的影响

在采样间距Δ为0.5，1.0，1.5，2.0，2.5，3.0 mm时分别计算JRC=16.7曲线的粗糙度指标cΔ值见表2。

表2 标准JRC=16.7曲线在不同采样间距下的c值Table 2 Value of c of JRC=16.7 standard JRC profile with different sampling interval

由表2可知随着采样间距Δ的增大c值减小，原因是采用较大间距分析曲线粗糙度时，较小尺度的粗糙度被掩盖了。天然节理具有自仿射分形特征[19]，基于分形理论[20]，建立一个分形模型，即假设指标cΔ与采样间距Δ满足幂定律:

cΔ=c0Δβ

(9)

其中，c0，β均为分形参数，分形维数D=1-β。两边取自然对数得

lncΔ=lnc0+βlnΔ

(10)

分析表2中lnΔ与lncΔ的关系如图6所示。

图6 ln Δ与ln cΔ的关系Fig.6 Relationship between ln Δ and ln cΔ

由图6可知，粗糙度参数c与采样间距之间的关系满足式(10)形式，显示指标c具有分形特征。分形参数可以反映出形貌线自相似的特点。利用分形特征，已知特定形貌线两个不同尺度的粗糙度指标c，可以预测其他任意尺度的c值。

在上述基础上计算得到10条标准JRC曲线的分形维数D见表3。

表3 10条标准JRC曲线的D值Table 3 Value of D of each standard JRC profile

4.2 不受采样间距影响的粗糙度评价系统

上述分析反映形貌线在某一测量间距下尺度比测量间距更小的粗糙度将被掩盖，而小尺度的粗糙对于抵抗剪切的贡献不应被忽略[21]。图6中截距lnc0是拟合直线上测量间距为单位1时粗糙度指标c的自然对数值，分形粗糙度维数D则表征了不同尺度粗糙度之间的相对关系，采用2个分形参数可以统一描述节理的粗糙程度，并且这2个参数与测量尺度无关。因此可提出与测量尺度无关的岩石节理粗糙度描述系统cn(c0,D)。分析c0D与JRC之间的关系如图7所示。

由图7可知，随着JRC的增大，c0D在增大并且反映了良好的线性关系，因此可得:

JRC=0.886c0D+2.035

(11)

岩石节理粗糙度描述系统cn(c0,D)充分考虑了形貌面微凸体剪切特性，可表示出形貌面方向异性同时不受测量尺度限制。

5 指标c延拓至三维形貌面情况

二维粗糙度指标获取方法简便，在不借助三维扫描仪的情况下即可快速获取，但不能全面描述节理形貌特征。若借助光学非接触式形貌扫描仪获得节理所有微元节点的位置坐标，并参考图5原理将三维形貌处理为长方体微凸体网格，则该二维粗糙度指标可以很容易拓展到三维形貌面情况。三维形貌面的粗糙度指标c可按式(12)计算。

(12)

将沿剪切方向数据定义为行数据，垂直于剪切方向为列数据。式中，Zi，j为第i行第j列网格高度坐标;Ni为沿剪切方向长方体网格的个数;Lj为第j列沿剪切方向节理长度;Nj为垂直于节理剪切方向的长方体网格个数。

以花岗岩节理为例计算三维剪切粗糙度指标c。花岗岩节理由花岗岩试件通过巴西劈裂法得到，节理平面尺寸为10 cm×20 cm。首先采用三维激光扫描仪对节理表面形貌进行扫描得到形貌数据点坐标，扫描间距设为1 mm;其次，基于扫描得到的形貌数据，建立节理面形貌网格;最后，编制程序计算节理的三维粗糙度参数c0与D。节理三维形貌面及4个剪切方向粗糙度指标c0与D如图8所示。不同的剪切方向对应不同的三维粗糙度指标c0与D，可见指标c0与D可以很好的表示出岩石形貌方向异性。

图8 节理三维形貌面及4个剪切方向粗糙度指标c0与DFig.8 Map of the rock surface and the roughness param- eters c0 and D

6 结 论

(1)在长方体微凸体2种破坏模式的基础上，通过合理的确定每一个长方体微凸体的计算高度提出一个新的描述节理形貌面粗糙度的指标c。粗糙度指标c不仅可以客观合理的定量描述节理形貌面粗糙度特征，还可以反映节理剪切方向性，同时发现指标c具有分形的特点。

(2)基于分形思想，采用2个分形参数可以统一描述节理的粗糙程度，并且这2个参数与测量尺度无关。提出了与测量尺度无关的岩石节理粗糙度描述系统cn(c0,D)。

(3)分析了粗糙度描述系统cn(c0,D)与JRC之间的关系，证明cn(c0,D)可与节理剪切强度建立关系。

(4)新指标在获取节理三维形貌坐标后可拓展为三维粗糙度指标，通过计算真实节理的三维粗糙度指标c0与D验证新指标可反映三维形貌方向异性特点。