基于容积粒子滤波的交互式声源鲁棒跟踪方法*
曹 洁, 吴尧帅, 李 伟2,, 王进花
(1.兰州理工大学 计算机与通信学院,甘肃 兰州 730050; 2.甘肃省制造业信息化工程研究中心,甘肃 兰州 730050;3兰州理工大学 电气工程与信息工程学院,甘肃 兰州 730050)
0 引 言
基于麦克风阵列的声源跟踪技术,一直是声学领域重要的研究课题,可广泛应用在电视电话会议[1]、海洋侦察[2]、智能机器人[3]等领域。传统的声源跟踪方法是连续的声源定位,但受不定因素的影响,声源位置的估计存在较大误差[4],致使跟踪算法精度较低。近些年,建立状态空间的跟踪方法被提出,比传统的连续声源定位方法跟踪效果更稳健。
声源状态空间相当于一个动态非线性系统,基于贝叶斯框架的滤波算法是解决声源跟踪的最常用方法。Dvorkind T G等人[5]利用扩展卡尔曼滤波(extended Kalman filtering,EKF)进行声源跟踪,改善了跟踪效果。但扩展卡尔曼滤波是利用一阶泰勒级数对非线性系统线性化,均值与方差的递推估计误差较大,致使跟踪误差较大。胡振涛等人[6]在容积卡曼滤波(cubature Kalman filtering,CKF)框架下实现对动态声源波达方向(direction of arrival,DOA)的自动跟踪,效果较好,但需要依靠矢量传感器本身固有的方向敏感性。Kawanishi M等人[7]将粒子滤波(particle filtering,PF)应用到三维空间的声源跟踪中,取得了一定效果。Zhong X等人[8]提出了基于扩展卡尔曼粒子滤波(extended Kalman PF,EKPF)的声源跟踪算法,减轻了混响对跟踪效果的影响。文献[5~8]均是将改进的贝叶斯滤波跟踪算法引入到声源跟踪中,在声源持续移动情况下,运动轨迹估计效果较好,但在有静音期出现的交互式声源[9]运动场景时,跟踪系统的鲁棒性较差。Lehmann E A等人[10]将静音检测(voice activity detector,VAD)融合到粒子滤波声源跟踪算法中,有效减小了静音造成的跟踪误差,但当静音期较长时,极易跟丢目标。
基于上述分析,本文提出了一种基于容积粒子滤波的交互式声源跟踪方法,并通过仿真实验验证了本文方法的有效性。
1 基于粒子滤波的声源跟踪框架
1.1 声源运动模型
当目标声源在空间中运动时,其状态信息可由多种状态模型表示,其中,Vermaak J等人[11]提出的郎之万(Langevin)模型结构简单,易于实现,在实际应用效果较好。在郎之万模型中,构建一个关于声源的笛卡尔坐标系,沿x方向、y方向以及z方向是独立同分布的。
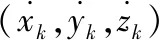
(1)
令rk=[xk,yk,zk]T表示k时刻声源的位置信息,则
(2)
声源的状态信息可以由以下的离散方程来描述[12]
(3)
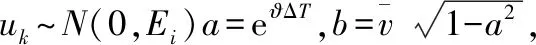
1.2 声源跟踪框架
麦克风阵列接收的音频信号不仅包含时频信息,也包含声源的空间信息。以麦克风阵列中心为坐标原点构建笛卡尔坐标系,利用各路音频信号得到麦克风之间的到达时间差(time difference of arrival,TDOA),再采用最小二乘算法得到当前时刻的坐标[13]。此坐标便可作为目标声源的量测信息,郎之万模型描述声源的运动特征,选择先验概率密度作为重要密度函数,将重采样[14]加入到框架中以减轻粒子退化对状态估计的影响,最终可得到一个基于粒子滤波的声源跟踪框架。其基本步骤如下:
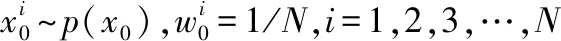
2)迭代:k=1,2,3…
a.利用声源定位算法得到量测信息zk;
c.利用粒子滤波算法更新权重,并归一化权重;
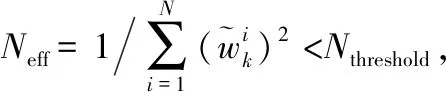
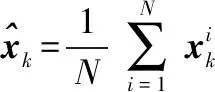
2 基于容积粒子滤波的交互式声源跟踪框架
2.1 容积粒子滤波
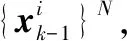
设置基本容积点
(4)
式中j=1,2,3…,2ξ,ξ为系统的状态维数,E为单位矩阵。
(5)
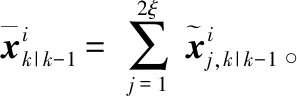
k时刻的状态误差协方差矩阵
(6)
(7)
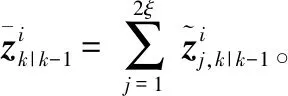
k时刻的量测误差协方差矩阵
(8)
k时刻的互相关协方差矩阵
(9)
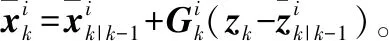
2.2 交互式声源跟踪框架
在交互式声源跟踪中,如果目标声源在静音期移动位置,当目标声源重新出现时,再将静音期之前的先验信息融合到状态空间中,会影响跟踪精度,甚至估计出的运动轨迹严重偏离目标。因此,长时间的静音期之后,舍弃之前的先验信息,重置跟踪算法参数,将会有效改善这一现象。
本文将位置移动判定因子ψ加入到交互式声源跟踪框架中,判断声源位置在静音期前后是否移动
ψ=Sgn(‖xp-xq‖2-ε)
(10)
式中 Sgn(·)为符号函数,xp为静音期之前状态的估计值,xq为静音期之后声源定位结果,ε为判定阈值。若ψ=1,则判定目标声源已经移动,将当前帧的声源定位结果作为初始状态,p(xq)粒子采样。然后跟新迭代;若ψ≠1,则判定目标声源未移动,状态更新继续按照静音期之前迭代。本文基于容积粒子滤波的交互式声源跟踪流程如图1所示。其中,N(·)为高斯函数,km为所选取的音频信号的总帧数,若要进行实时跟踪,则令km=+∞。
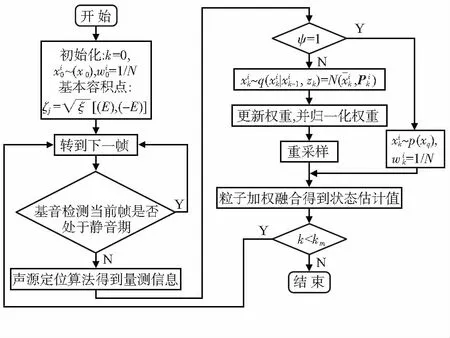
图1 交互式声源跟踪流程
3 实验分析
3.1 实验环境

图2 八元圆形麦克风阵列
3.2 性能指标
本文采用均方根误差(root mean square error,RMSE)度量跟踪效果,定义为
(11)
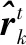
3.3 实验结果
为验证本文提出方法的有效性,分别在动态声源与交互式声源环境下,与文献[7]中基于粒子滤波算法的声源跟踪方法,文献[8]提出的基于扩展卡尔曼粒子滤波的声源跟踪方法作对比。在不同的信噪比下,对比3种跟踪算法的跟踪效果。其中,信噪比以5 dB为步长从5 dB到30 dB,3种方法分别进行50次蒙特卡洛实验。
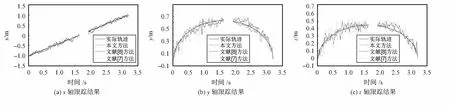
实验1动态声源。如图3所示为实验中目标声源的路径轨迹。沿曲线x2+y2+z2=1,y=2z,y≥0移动,以坐标(-1,0,0)m为起点,坐标(1,0,0)m点结束。图4为不同信噪比下3种跟踪方法的RMSE值,图5为SNR=30时3种跟踪方法对动态声源跟踪效果。
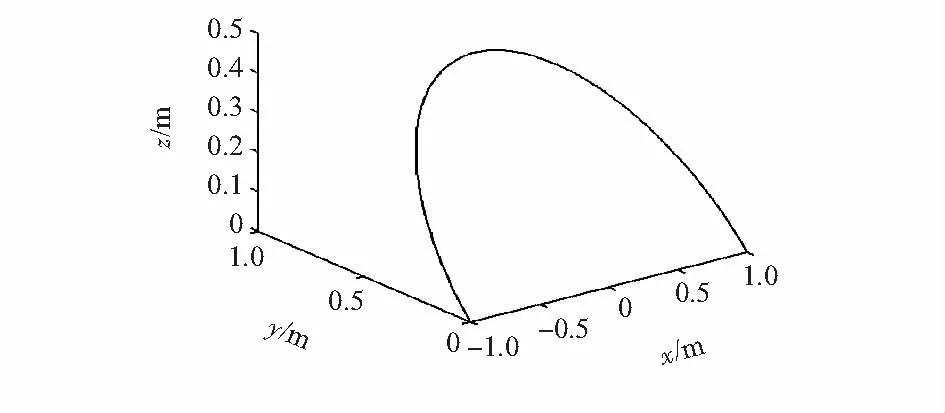
图3 声源运动轨迹
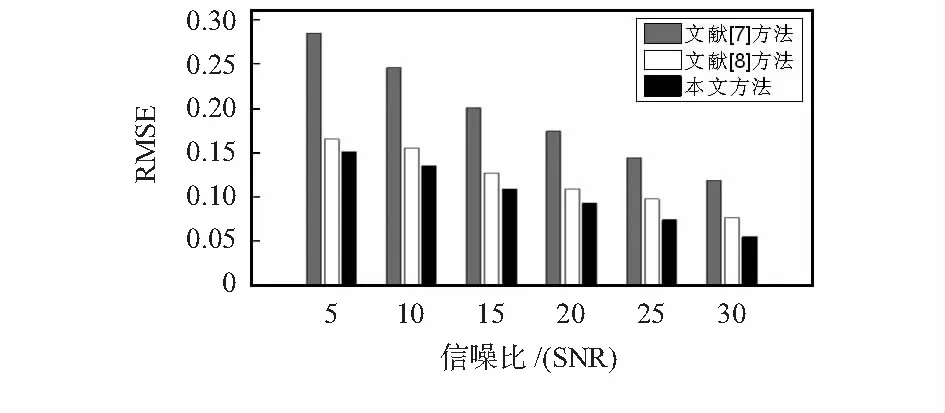
图4 不同信噪比下3种跟踪方法的RMSE值
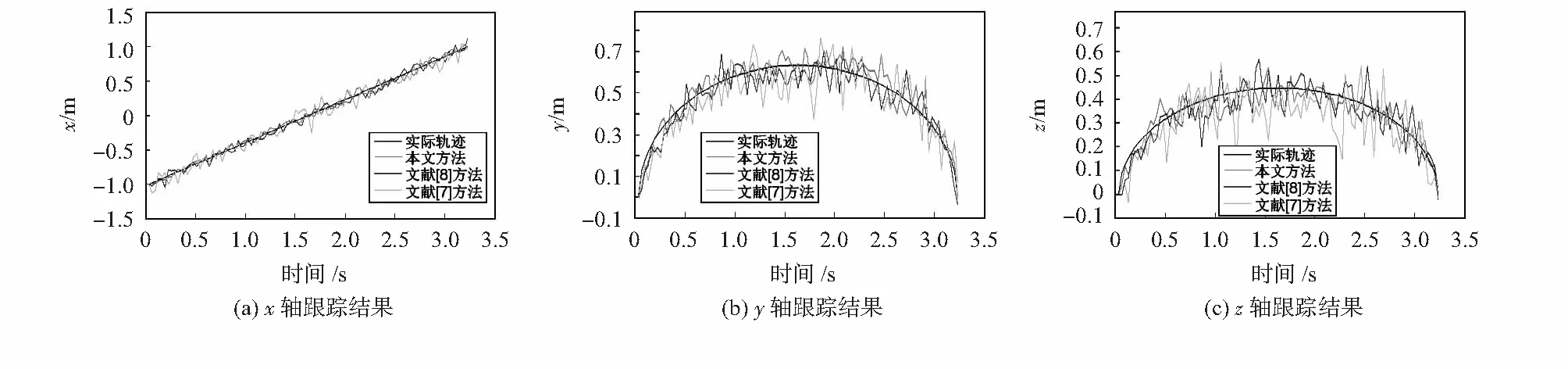
图5 SNR=30时3种跟踪方法对动态声源跟踪效果
从图4中可以观察到,在不同的信噪比环境下,本文算法的RMSE均比文献[7]方法的RMSE减小50 %左右,均比文献[8]方法的RMSE减小10 %以上。而且随着信噪比的提高,3种方法的RMSE均在减小,文献[7]方法在SNR=30 dB环境下的RMSE比SNR=5 dB下的减小了58.2 %,文献[8]方法在SNR=30 dB环境下的RMSE比SNR=5 dB下的减小了53.4 %,本文方法在SNR=30 dB环境下的RMSE比SNR=5 dB下的减小了63.6 %。由于本文方法选取了更加合适的重要密度函数,粒子状态更加接近真实目标,收敛速度明显高于文献[7]方法、文献[8]方法,如图5所示。综合图4和图5可知,在不同的背景噪声环境下动态声源跟踪中,本文跟踪方法均优于文献[7]方法、文献[8]方法;且随着信噪比的提高,本文方法跟踪效果提升速率也高于其他两种跟踪算法。
实验2交互式声源。如图6所示为实验中目标声源的路径轨迹表达式同图3。
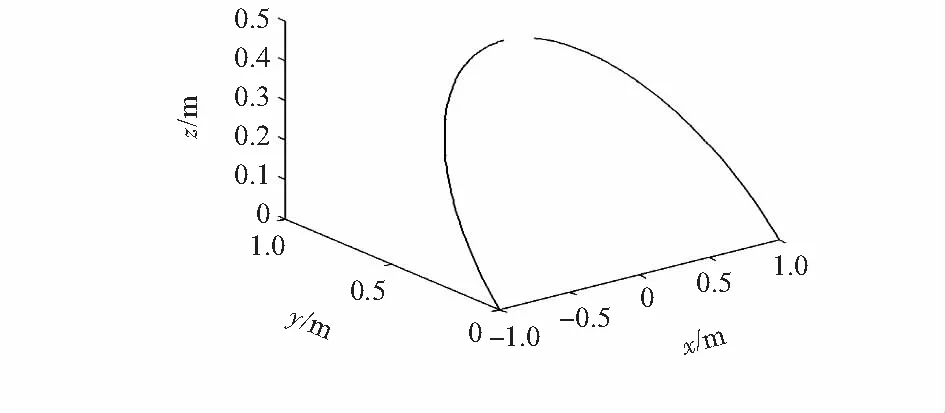
图6 交互式声源运动轨迹
其中,0 图7 不同信噪比下3种跟踪方法的RMSE值 从图7中可知,在不同的信噪比环境下,本文算法的RMSE均比文献[7]方法的RMSE减小55 %以上,均比文献[8]方法的RMSE减小50 %以上。而随着信噪比的提高,只有本文方法的RMSE一直在减小。由于文献[7]方法与文献[8]方法融合了静音期之前的先验信息,致使两种方法在静音期结束后的跟踪误差变大,而本文方法舍弃了错误的先验信息,因此仍能保持较好的跟踪效果,如图8所示。综合图7和图8可知,本实验验证了在不同的背景噪声环境下交互式声源跟踪中,本文跟踪方法优于文献[7,8]方法。 图8 SNR=30时3种跟踪方法对交互式声源跟踪效果 本文提出了一种基于容积卡尔曼粒子滤波的交互式声源跟踪方法。相对于基于粒子滤波的声源跟踪方法,该方法通过容积卡尔曼处理粒子,得到对应的重要密度函数,增强了最新量测信息对粒子的修正作用;同时,通过引入移动判定因子,构建了交互式声源跟踪框架,有效减轻了静音期对声源跟踪系统的影响。理论分析和实验结果均证明了本文提出的方法的优越性。下一步的工作将研究如何将本文定位方法与定向语音增强技术相结合,跟踪特定目标声源。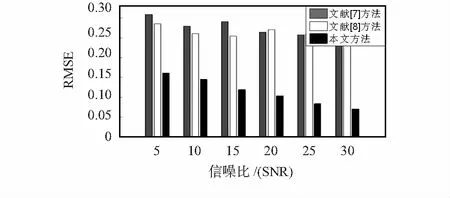
4 结 论

