一种基于Contourlet变换的总变分图像去噪算法

张洪为，张俊英

图像去噪是图像被进一步研究和处理的基础，如何在去除图像噪声的同时保护图像的纹理和细节是图像去噪的关键问题.现有的去噪方法一种是基于频域的去噪方法，包括傅里叶变换、小波变换［1］、Contourlet［2］变换等，即先将含噪图像变换到频率域，然后根据噪声主要位于变换域的高频部分，利用硬阈值或软阈值方法对图像的高频部分进行处理，最后进行反变换即得到去噪后的图像.一种是基于空间域的去噪方法，包括均值滤波［3］、中值滤波［4］、偏微分方程［5-6］、变分法［7］等.均值滤波和中值滤波是利用噪声点周围像素点的均值或中值进行去噪，是一种邻域方法.偏微分方程和变分法是将一个图像去噪问题转化为求解一个偏微分方程问题或泛函极小化问题，具有局部自适应性、模型建立的灵活性等诸多优点.本文针对阈值去噪方法容易产生伪吉布斯现象和阈值选择困难等局限，将总变分去噪方法与Contourlet变换结合，提出一种基于Contourlet变换的总变分图像去噪方法.

1 Contourlet变换

Contourlet变换是 Do和 Vetterli［8-9］于 2002 年提出的一种新的多尺度几何分析方法，也称为金字塔方向滤波器组PDFB（Pyramidal Directional Filter Bank），PDFB的实现包括两个过程，即首先对图像进行拉普拉斯塔式分解LP（Laplacian Pyramid），捕获奇异点，然后由方向滤波器组DFB（Directional Filter Banks）对获得的带通图像进行分解，以捕获方向信息.重复上述过程，将图像分解为多尺度方向子带如图1所示.Contourlet变换由于具有多方向滤波器组，从而它比小波变换具有更多的方向信息.图2为Zoneplate图像经过Contourlet变换后的系数图像，各尺度由粗到细依次具有4、4、8、8个方向子带.

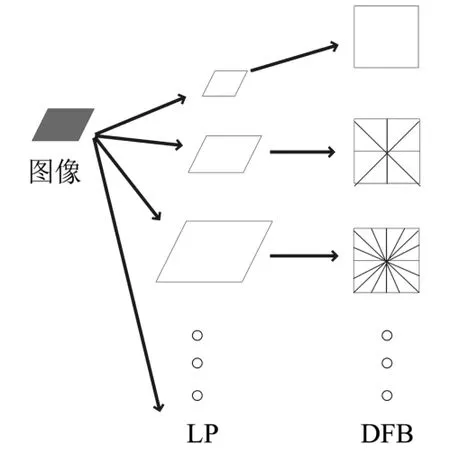
图1 图像进行PDFB变换过程示意图

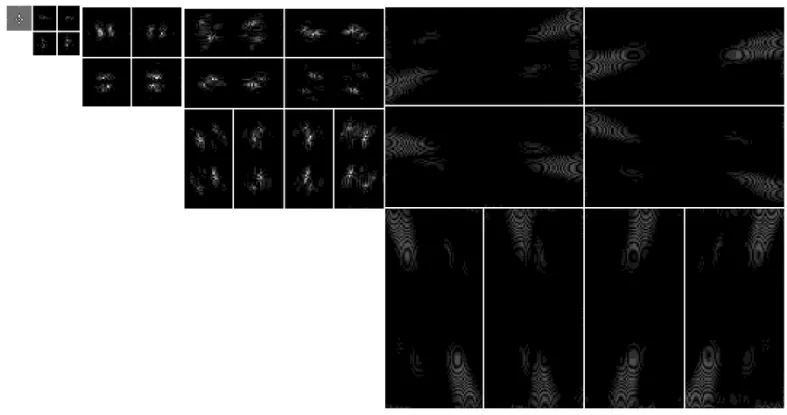
图2 Zoneplate图像的Contourlet分解示例图

2 基于Contourlet变换的阈值去噪方法

基于Contourlet阈值去噪方法是将经过Contourlet变换的Contourlet系数按照事先选定的阈值分为两类，当Contourlet系数C的绝对值大于等于事先选定的阈值Th时，说明这部分系数主要由噪声等高频信息变换而来，去噪时通常被舍弃；当Contourlet系数C的绝对值小于事先选定的阈值Th时，说明这部分系数主要由原始图像的低频信息变换而来，去噪时通常被保留.具体如式（1）所示

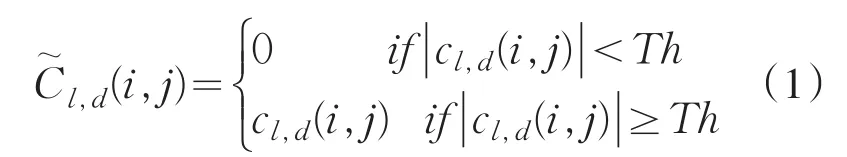
Contourlet变换的硬阈值法虽然能很好的保留图像的边缘等细节信息，但它的局限性也是显而易见的.因为硬阈值函数在阈值处不连续，造成重构图像信号产生震荡，所以经过硬阈值去噪的图像通常会出现局部振铃和伪吉布斯效应.

3 总变分去噪方法

变分法图像去噪的基本思想是将图像去噪问题归结为一个泛函极小化问题，然后进一步求解相应的微分方程，1992年Rudin Qsher和Fatemi［10］提出变分极小化模型（简称TV模型）如下

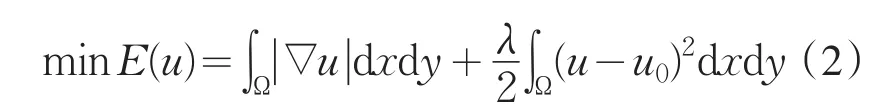
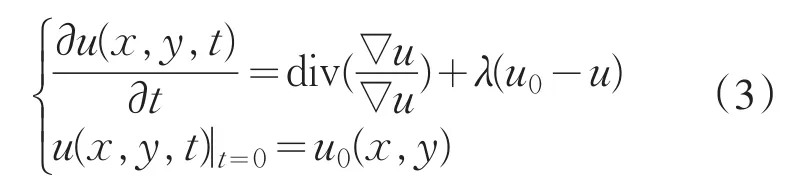
其中，(x,u)∈Ω,t＞0.尽管TV模型在保持图像边缘方面有比较好的特性，但随后的研究发现它不完全符合形态学原则［11］，这一局限性导致其稳态解中常会出现明显的“阶梯”效应.另外，由于TV 模型是以为扩散系数的，在图像的边缘附近，因较大较小，扩散较弱，从而保留了边缘，但对于边缘附近的噪声却很难去除.

4 基于Contourlet变换的总变分去噪算法

由于基于Contourlet变换的阈值去噪方法存在阈值选择困难及容易产生伪吉布斯效应等局限，而总变分去噪模型的局限性是易于产生“阶梯”效应，为此提出一种基于Contourlet变换的总变分去噪算法，即在基于Contourtlet变换的阈值去噪方法中，用总变分模型扩散过程代替阈值过滤噪声过程，具体算法如下:

1）确定分解的层次K，对含噪图像进行Contourlet变换，得到低频系数a0和高频系数d0,d1,…,dK-1.

2）对变换域的最外两层利用总变分模型式（3）进行扩散处理，得到新的系数.

3）对未处理的高频系数d0,d1,…,dK-3和已处理的高频系数dK-2,dK-1以及低频系数a0进行Contourlet逆变换，得到信号x̂，即为原始信号x的估计.

5 实验结果

图3 噪声强度为15的Lena图像去噪结果比较

图4 噪声强度为15的Barbara图像去噪结果比较

为验证本文方法的有效性，本文选取了大小为256×256的Lena、Barbara两幅图像作为测试图像，并将本文方法与基于Contourlet的硬阈值去噪方法和总变分去噪方法在强度为15的高斯白噪声下的去噪结果进行比较，实验结果表明，利用基于Contourlet的阈值去噪方法去噪后的图像会产生明显的伪吉布斯效应，利用总变分模型去噪后的图像会丢失很多的纹理细节信息并且会出现明显的块效应，而利用本文算法去噪后的图像既能很好的去除噪声，又能很好的保留图像的纹理和细节信息.噪声强度为15的Lena图像去噪结果比较如图3所示，噪声强度为15的Barbara图像去噪结果比较如图4所示.

6 结论

本文针对Contourlet阈值去噪方法和总变分去噪方法的局限性，提出了一种基于Contourlet变换的总变分去噪方法，实验表明，该方法在去除图像噪声的同时能够保持图像的纹理和细节信息.