一种基于颜色读数的物质浓度测量模型

蒲宝卿，刘代娜

比色法是目前常用的一种检测物质浓度的方法，即把待测物质制备成溶液后滴在特定的白色试纸表面，等其充分反应后获得一张有颜色的试纸，再把该颜色试纸与一个标准比色卡进行对比，就可以确定待测物质的浓度档位了.本方法广泛应用在科学实验、医药卫生、农业生产等领域，比如矿物质中锑含量的测定、金黄色葡萄球菌肠毒素B的检测、牛乳中蛋白质的含量测定等［1］.

然而此类研究大部分注重的是溶液配制、光波吸收度对物质浓度的影响，使用比色卡颜色读数来测量物质浓度的研究较少，而且由于每个人对颜色的敏感差异和观测误差，使得这一方法在精度上受到很大影响.随着照相技术和颜色分辨率的提高，希望建立颜色读数和物质浓度的数量关系，即只要输入照片中的颜色读数就能够获得待测物质的浓度［2］.

1 数据分析与基本模型

1.1 数据分析

根据5种物质:组胺、溴酸钾、工业碱、硫酸铝钾、奶中尿素，在不同浓度下的颜色读数［2］，分别建立五种散点图观察分析.例如对第一种物质组胺建立颜色读数和浓度（ppm）的平滑散点关系图（见图1），发现二者之间的线性关系明显.

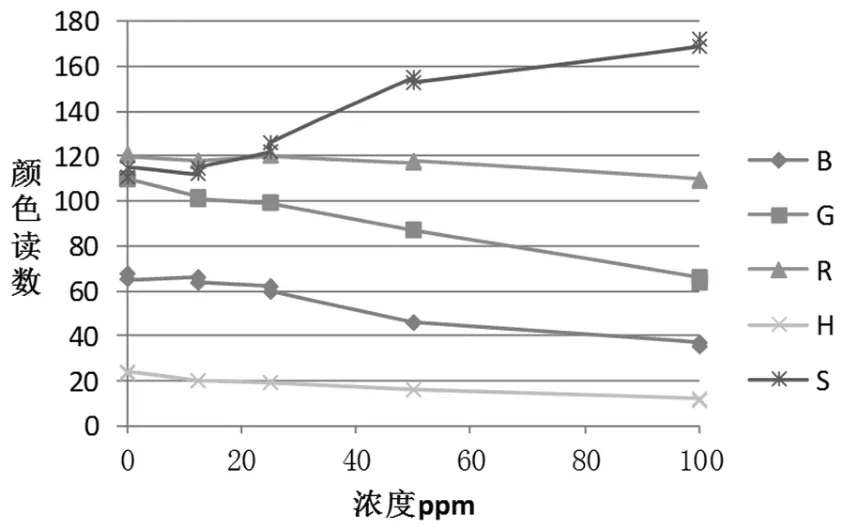
图1 组胺浓度和颜色读数的关系

利用同样的方法分析其余四组数据:

1）溴酸钾溶液浓度与饱和度色卡读数存在显著的正相关性，浓度在0～25ppm之间时读数变化幅度最大.

2）工业碱溶液浓度在0～8ppm之间时颜色读数基本没有变化，浓度在8～12ppm之间时读数变化幅度大.

3）硫酸铝钾溶液浓度在0～2ppm之间时颜色读数有较明显变化，浓度在2～5ppm之间时颜色读数基本没有变化.

4）奶中尿素溶液浓度在0～2500ppm之间变化时（浓度变化区间相对前四种物质区间很大），但是颜色读数基本没有变化或者变化幅度很小.

通过分析发现除了色调H与物质浓度变化关系不太明显以外，其余四项读数蓝色颜色值B、绿色颜色值G、红色颜色值R、饱和度S与物质浓度的线性关系明显，尤其是和饱和度S正线性相关关系最为显著.

1.2 构建物质浓度与颜色读数关系模型

通过以上分析发现，虽然各种物质浓度受不同读数的影响程度不同，但总体来讲都有影响.现假设物质浓度用符号C表示，物质浓度与颜色读数的各个不同颜色读数之间关系可表示为

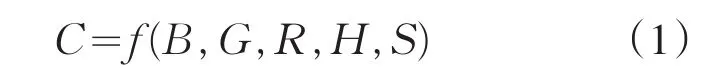
首先讨论特殊情况:在测定组胺、溴酸钾、工业碱、硫酸铝钾、奶中尿素等五种物质浓度时，待测物质浓度为0时的颜色读数如表1所示.

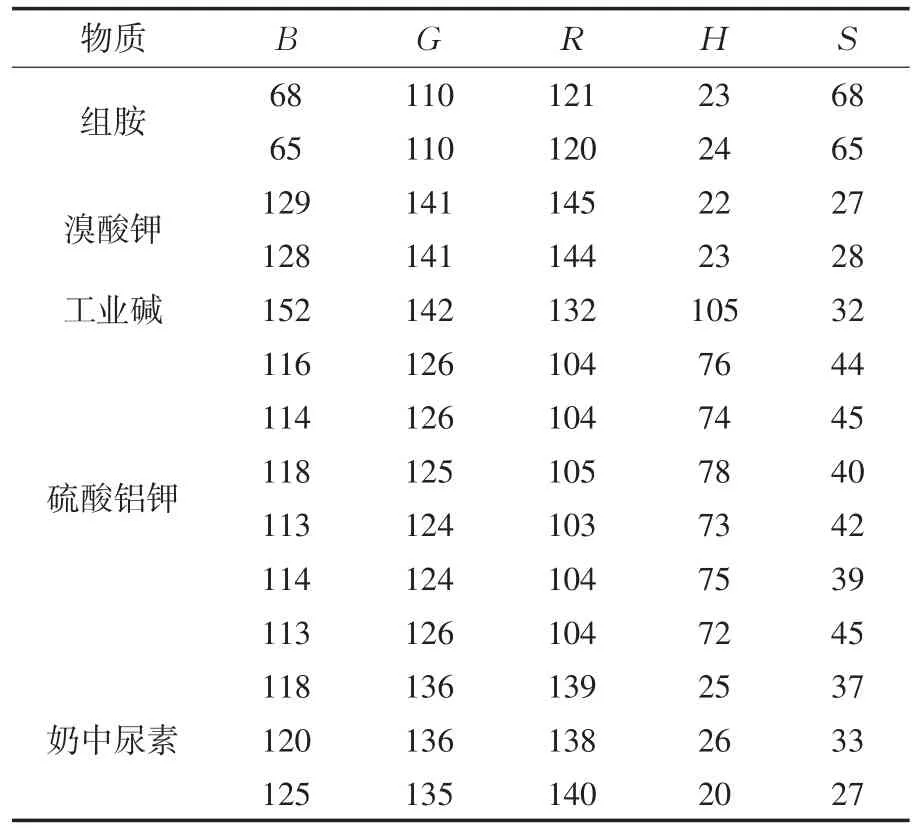
表1 浓度为0时颜色读数对比

从表1可以看出，不同物质溶液在浓度为0的情况下颜色大不相同，甚至同种物质浓度为0时的读数也不尽同.引起这些测试结果的原因是由于不同物质的测试试纸的差异、同种试纸反应误差、对照试纸时的光线强弱不同等原因造成的.通过对比发现，同种物质的读数有变化但不是很大，而不同物质之间的读数差别非常大，这说明测定不同物质的试纸，颜色读数随物质浓度变化的规律不同，需要分别针对每种物质构建颜色读数与物质浓度模型.

1.3 模型构建中存在的问题

1）存在非线性关系.颜色读数和物质浓度之间可能存在非线性关系，例如工业碱颜色读数和浓度之间的关系.通过变化图可以看出颜色读数和浓度之间明显不是线性关系.

2）数据量太少引起过度拟合问题.由于测量中得到的数据量太少，数据观测次数也太少.例如溴酸钾、组胺两种物质只测定了5种不同的浓度，每种浓度测量数仅为2.工业碱虽然测了7种不同浓度，但是测量次数仅为1次.根据一般数据统计的规律，数据量太少而自变量过多时，很容易出现过度拟合问题［3］.过度拟合是指为了得到一致假设而使假设变得过度严格，基于这样的数据建立的模型不具有普遍适用性.避免过度拟合通常采用增大数据量和测试样本集的方法.

1.4 使用相对标准偏差评价数据优劣

评价数据优劣可以采用灰色相关性、层次聚类等方法分析.但最终都是要判断误差大小，对于某种特定物质而言，同种浓度下的颜色读数之间差别是由误差造成的，差别越小则数据质量越高［4］.本文中使用相对标准偏差来评价比色方法的精密度，所有标准偏差值的均值可作为数据整体质量好坏的评价标准.

2 模型假设

针对颜色读数与物质浓度的关系，我们假设以下两种模型.

2.1 多元线性模型

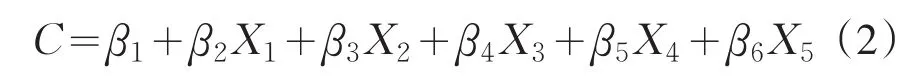
其中，C:物质浓度，X1:蓝色颜色值B，X2:绿色颜色值G，X3:红色颜色值R，X4:色调H，X5:饱和度S，β1为常量，β2、β3、β4、β5、β6均为系数.

2.2 非线性模型

其中，C:物质浓度，X:降维后确定的颜色值，a为系数，b为X的指数.

3 模型的建立与求解

3.1 数据处理

由于给出的数据有可能出现异常，所以首先进行数据预处理.按照第一题中的方法分析数据质量，分别计算不同浓度下每种颜色维度的相对标准偏差RSD值，计算结果如表2所示.

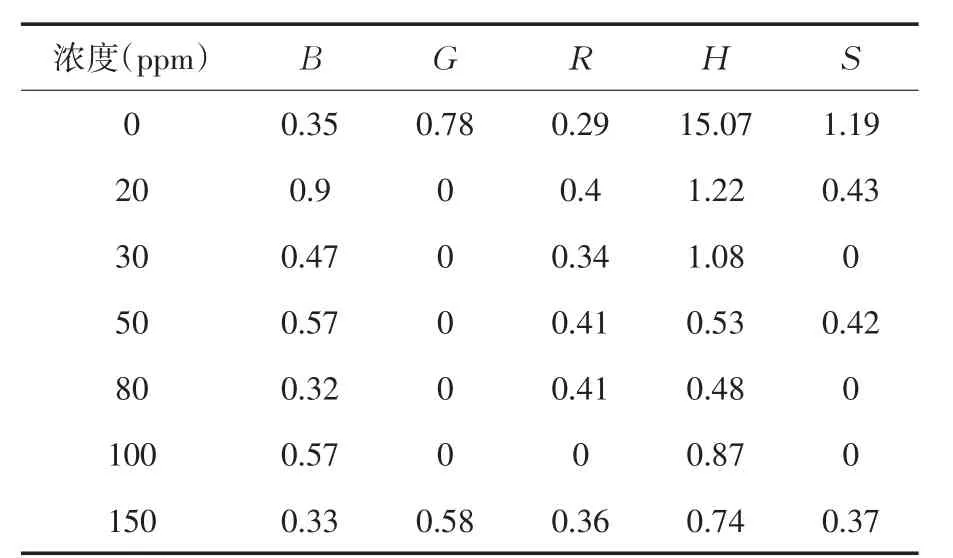
表2 二氧化硫各种颜色维度RSD值（%）

表2中所有RSD的均值为0.8423，其中四项RSD值大于1，如上表对应的异常值.通过对二氧化硫不同浓度的测量数据［2］分析可知，有三次测量值存在严重误差，如表3所示.

表3 异常数据项

表3中去除异常数据后浓度为0时色调H的RSD值为2.9425，浓度为0时饱和度S的RSD值为0.4225，平均RSD值变为0.4736，远低于原始数据0.8423，由此可见，去掉异常数据后，数据质量得到明显提高.

3.2 模型的构建

由前面的分析发现，用单纯的多元线性回归拟合效果可能不好.考虑分别采用多元线性模型、非线性模型分析浓度与各颜色维度之间的关系，比较后得到较优的模型.

1）多元线性模型.首先去掉三次异常数据后构建一个多元线性模型.在Excel中进行多元线性回归得到的结果

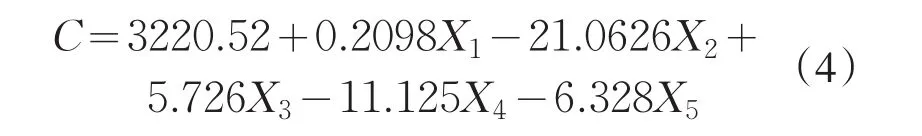
本次线性回归分析中，R2=0.878，标准误差RMSE达到20.14，整体拟合效果不是很好.本次回归涉及到五个颜色维度，不同颜色维度之间可能存在一些相互关联，比如色调与红、蓝、绿有关系，饱和度同样与红、蓝、绿三种颜色有关，这样很难避免多重共线性问题.多重共线性是指线性回归模型中的解释变量之间由于存在精确相关关系或高度相关关系而使模型估计失真或难以估计准确.一般来说，由于数据的限制使得模型设计不当，导致设计矩阵中解释变量间存在普遍的相关关系［5］.可以用逐步回归法解决多重共线问题.

2）非线性模型.通过前面多元线性回归发现色调值与浓度之间的变化关系比较明显，可以考虑建立非线性关系模型.在Matlab中采用拟合方法构建二氧化硫浓度与色调读数之间的模型，如图2所示，相关参数如表4所示.

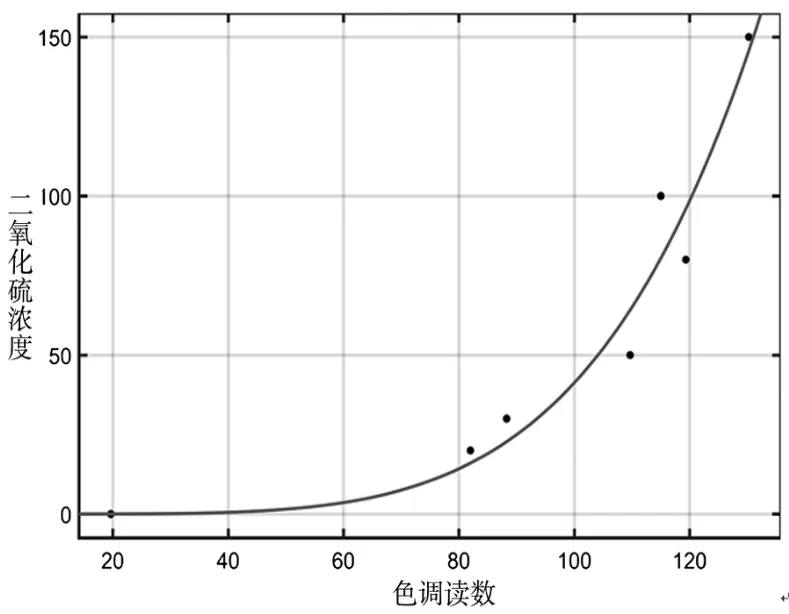
图2 二氧化硫浓度与色调读数关系拟合

表4 非线性模型拟合参数

本次拟合中，R2的值达到0.9433，RMSE的值为13.59，拟合效果比第一种要好.

3.3 模型误差分析

4 结论

数据量和颜色维度对模型的影响有两方面:多重共线性和过度拟合.当数据量多而颜色维度少时模型将没有足够的解释能力；当数据量少而颜色维度较高时会造成过度拟合问题.本文在处理过程中通过逐步回归的方法进行降维处理，最后得到的非线性模型要优于线性模型.